Итак, разбор задач. Сразу уточню, что задачу MikeMirzayanov не угадал никто (неплохо мы замаскировались, а?) — это была задача C про переборчивую корыстолюбивую принцессу. Собственно, с этой задачи раунд и начался, все остальные я придумала уже для продолжения темы.
Общее количество драконов D может быть достаточно небольшим, поэтому задачу можно решать без затей, перебором драконов от 1 до D и проверкой каждого дракона отдельно. Сложность решения — O(D). Существует более идейное решение со сложностью O(1), основанное на формуле включения-исключения. Для каждого из четырех критериев избиения драконов считаем количество драконов, которые под него подпадают, т.е. чей номер кратен соответствующему числу. Затем считаем количество драконов, которые подпадают под пары, тройки и четверки критериев, т.е. чей номер кратен наибольшему общему кратному соответствующих наборов чисел. Количество чисел от 1 до D, кратных T, равно D / T. Наконец, количество пострадавших драконов равно количеству драконов, подпадающих под один критерий, минус количество драконов, подпадающих под два критерия, плюс количество драконов, подпадающих под три критерия, и т.д. Этим методом пришлось бы воспользоваться, если бы общее количество драконов было слишком большим для итерирования по нему.
В этой задаче достаточно было в точности воспроизвести последовательность событий, происходящих на прямой от пещеры до замка. В моем решении основной единицей были события "дракон в пещере и собирается вылетать, принцесса где-то на прямой" и "дракон догнал принцессу" — тогда достаточно отслеживать время и координату принцессы. Впервые событие первого типа произойдет в момент T, когда принцесса отбежит на T * Vp от пещеры. Если при этом она уже добралась до замка, драгоценности не понадобятся. Иначе можно начинать цикл: промежуток времени, через которое произойдет событие второго типа, равно расстоянию от пещеры до принцессы, разделенному на разность их скоростей. Передвигаем принцессу на расстояние, которое она успеет пробежать, и проверяем, не попался ли по дороге замок. Если нет, то дракон успеет ее догнать — бросаем что-нибудь блестящее. Второе действие цикла — посчитать промежуток времени, через которое произойдет событие первого типа, то есть дракон вернется в пещеру; он равен новой координате принцессы, деленной на скорость дракона, плюс время наведения порядка в сокровищнице. Передвигаем принцессу еще раз и возвращаемся к началу цикла.
Сложность алгоритма оценить можно из интуитивных соображений: больше всего итераций понадобится при максимальных скорости дракона и расстоянии до замка и минимальных скорости принцессы и временах задержек. У меня получилось что-то около 150 драгоценностой и столько же итераций.
Изначально эта задача была скучной учебной задачей про вытаскивание черных и белых шаров из мешка. Но сами подумайте, откуда у дракона в пещере может взяться такой банальный предмет, как мешок шаров? А вот мешок мышек ему вполне может пригодиться — например, для запугивания принцессы или как легкая закуска.
Если бы мышки были шарами и не выпрыгивали из мешка, задача решалась бы довольно просто, итерацией без рекурсии. Пусть на каком-то шаге итерации в мешке остается B черных и W белых мышек и вероятность попасть в это состояние равна P (изначально P = 1, W и B равны начальным значениям). Вероятность вытащить белую мышь на этом шаге равна P * W / (B + W) (это уже не условная вероятность "при условии того, что мы находимся в этом состоянии", а абсолютная). Если очередь принцессы тянуть, то эта вероятность прибавляется к вероятности ее победы, если очередь дракона, вероятность победы принцессы не меняется. Для перехода на следующий шаг итерации нам нужно, чтобы игра не закончилась, то есть на текущем шаге вытащили черную мышь, и количество черных мышей уменьшилось, а вероятность попасть на новый шаг итерации умножилась на B / (B + W). Проитерировав так до того, как черные мыши закончатся, получим ответ.
Увы, мышки в мешке явно ведут себя не так флегматично, как шары. Это вносит элемент неопределенности — мы не знаем точно, в какое состояние перейдет игра после того, как дракон и принцесса вытянут своих мышей и перейдут на следующий этап игры. Поэтому решение должно быть рекурсивным (или динамическим программированием, кто как любит). Ходы принцессы и дракона обрабатываются аналогично, но после этого нужно скомбинировать результаты решения подзадач (W — 1, B — 2) и (W, B — 3). Код функции:
map<pair<int, int>, double> memo;
double p_win_1_rec(int W, int B) {
if (W <= 0) return 0;
if (B <= 0) return 1;
pair<int, int> args = make_pair(W, B);
if (memo.find(args) != memo.end()) {
return memo[args];
}
// we know that currently it's player 1's turn
// probability of winning from this draw
double ret = W * 1.0 / (W + B), cont_prob = B * 1.0 / (W + B);
B--;
// probability of continuing after player 2's turn
cont_prob *= B * 1.0 / (W + B);
B--;
// and now we have a choice: the mouse that jumps is either black or white
if (cont_prob > 1e-13) {
double p_black = p_win_1_rec(W, B - 1) * (B * 1.0 / (W + B));
double p_white = p_win_1_rec(W - 1, B) * (W * 1.0 / (W + B));
ret += cont_prob * (p_black + p_white);
}
memo[args] = ret;
return ret;
}
Сложность рекурсии с мемоизацией равна количеству разных пар аргументов, с которыми ее можно вызвать, т.е. O(WB).
Задача на динамическое программирование с предпросчетом.
Первая часть решения — для каждой полки предпросчитать максимальную стоимость i предметов, которые с нее можно взять (i от 1 до общего количества предметов на полке). Жадно это сделать нельзя; это можно увидеть на примере полки 6: 5 1 10 1 1 5.
Вторая часть — стандартная динамика по параметрам [номер последней учтенной полки][общее количество взятых предметов]. При переходе к следующей полке перебираются все возможные количества предметов, которые с нее можно взять, и общая стоимость взятого увеличивается на соответствующие стоимости (предпросчитанные).
Не забудь пожалуйста сказать о том, как следует понимать слово "любой" в задаче C, уж очень мне понравилось как меня проминусовали в теме самого контеста. Надеюсь и здесь пару сотен минусов огрести.
Нет ну серьёзно, кто так формулирует задачи? — "Каждый раз, когда она видит жениха более богатого, чем любой из предыдущих, она произносит сдержанное «Ах...»" Почему здесь слово "любой" должно восприниматься иначе чем "отговори любого из своих друзей от курения, и курящих станет меньше".
Решал в дорешке, понял правильно. В принципе, странно, что принцесса удивляется, увидев второго по нищенству жениха :) И потом, в значении "хотя бы кого-то" обычно пишется "некоторого другого", но явно не "любого другого".
Ну а теперь, строго говоря. Если во время контеста возник вопрос — понятно, что делать. Кроме того, понятно, что можно решить задачу для обоих пониманий условия одновременно (например, мое АС решение будет АС, если проверять "хотя бы одного раньше"). Достаточно маленького замечания автору "в следующий раз пишите условия немножко аккуратнее, пожалуйста!", а не 28 комментариев в каждом обсуждении.
По теме: как решать В в целых числах?
Нормально задача сформулирована, по-русски. Когда мне говорят "любой", это означает, что кого б я не поставил на это место, фраза будет верна. И в Вашей фразе, и у Nickolas это так (обе фразы остаются верны для любого из...).
Мне надоело уже приводить дурацкие примеры, лучше откройте словарь и посмотрите значение этого слова. "Получите двухпроцентную скидку в нашем магазине, если любая ваша покупка в прошлом месяце была больше тысячи рублей, и содержала любую продукцию компании кока-кола". Вы думаете, что каждая покупка должна быть больше 1000 рублей, и содержать всевозможную продукцию фирмы кока-кола?
Не совсем корректно сформулированным и двухсмысленным является как раз Ваш последний пример (зная маркетинговые подвохи, я бы подумал в магазине и уточнить — каждая покупка имеется в виду или хотя бы одна, потому как смысл слов говорит первое, а здравый смысл — второе).
"Чтобы отправить письмо, достаточно бросить его в любой почтовый ящик". "Чтобы проходить плановые медицинские осмотры, достаточно зарегистрироваться/завести карточку/быть зарегистрированным в любой городской поликлинике." Ты побежишь во все поликлиники своего города? Или ты считаешь это неверные предложения?
заметь, что у слова двоякое значение в первом предложении, с одной стороны оно говорит что подойдет каждый ящик, какой бы ты не выбрал, с другой стороны, ты не обязан закидывать письма во все почтовые ящики, чтобы их отправили адресату.
В этих примерах, чтоб я не подставил заместь "любой" (любой почтовый ящик, любую поликлинику) — фразы остаются верными (для каждого почтового ящика, верно то, что если в него брошено письмо — оно считается отправленным). Т.е. смысл слова "любой" такой точно как в задаче. Т.е. см. мой первый пост.
"Каждый раз, когда она видит жениха более богатого, чем любой из предыдущих, она произносит сдержанное «Ах...»" по вашему здесь нужно быть богаче каждого жениха.
"Каждый раз, когда я бросаю письмо в любой почтовый ящик, оно доходит адресату" а здесь, нужно бросить хотя бы в один.
Объясните мне, пожалуйста, КАК?
У меня почему-то мозг взрывается когда я пытаюсь понять по вашему). В случае с ящиками подходят все, а по вашему в случае с женихами — хотя бы один
ответ (снова поехали кнопочки в html)
Мне говорят "она видит жениха более богатого, чем любой из предыдущих" — чтоб это проверить, я перебираю всех предыдущих женихов.
Мне говорят "когда я бросаю письмо в любой почтовый ящик, оно доходит адресату" — чтоб проверить это, я перебирают все почтовые ящики. Т.е. эта фраза верна для каждого почтового ящика по отдельности. А слово "любой" в ней не означает "хотя бы один" — я делаю заключение, что Вы кидаете только в один ящик, потому, что Вы используете единственное число (а также руководствуясь здравым смыслом), а вовсе не из-за того, что Вы используете слово "любой". "Любой" в этом случае подчеркивает, что это верно для каждого почтового ящика, какой бы мне не пришёл на ум.
Логика понятна?
Мне то понятна, я согласен что слово любой имеет значение каждый, но оно также имеет значение некоторый, какой угодно, какой попало, хоть какой-нибудь.
ответ на сообщение KirillB, прямо ответить не могу, ибо поехали кнопочки и в FF и в Opera)
Подходят все женихи, но достаточно быть богаче одного, так же как с ящиками, все подходят, но письмо опустить нужно в один любой первый попавшийся.
Ну ладно, тут уж сто раз все это обсуждалось, возможно есть двусмысленность. Не буду дальше спорить — я изначально читал англ вариант. Хотя кажется логичней думать, что, как и с ящиками, должен подходить "любой первый попавшийся", что не гарантирует удачного выбора.
Действительно, можно понять слово "любой" двумя способами. Слава Богу есть первый сэмпл, по которому можно однозначно понять условие, но так быть не должно. Мария писала условия с уклоном на сказку, поэтому с целью лучшего звучания она использовала слово "любой". Как всегда браво тем "опытным" вычитывалщикам, которые работают в Codeforces. Вообще даже моего не самого большого опыта в разработке контестов достаточно, чтобы не допускать слов типа "любой" в условиях задач, когда имеется в виду "каждый". Тут ошибка создателей контеста очевидна. Если есть участники "в конкурсе", которые пострадали от этого, то правильно было бы перепроверить их решения на альтернативном наборе тестов. А так как этого точно не сделают (ни разу еще не делали), то еще раз обновлю свой счет: TopCoder 5 : 1 Codeforces
"Тесты являются частью условия задачи". Если не путаю, это говорит Корнеев каждый раз на северном четвертьфинале ACM.
Так оправдываются те, кто не умеет нормально писать условия. Написать недвусмысленное условие не так-то и сложно. Надо просто не вые#@%аться и уделять меньше времени легендам, а больше времени — самому условию задачи. Всем ведь по большому счету наплевать кто там — дракон, принцесса, Ктулху, Ciel или еще какая-нибудь ересь, но всем важно, что же требуется от него в задаче. Если хотя бы один человек обоснованно понял условие не так, как этого хотел автор, то это огромный минус автору и еще больший минус тем, кто вычитывал его условия (и не только его и уже не один десяток раз).
Формализация — часть процесса решения. Без драконов и принцесс это будет задача для кодера, а не для программиста.
Однако заметьте, что в данном случае формализация получается неоднозначная — в этом и вся проблема, не более.
Да, я это заметил. Но мне понадобилось несколько секунд, чтобы посмотреть тест и её разрешить.
если честно, я думаю, что это минус исключительно нынешней системе образования и тому, какой слабое место отводится знанию русского языка в высшем образовании =)
Заметь, что автор задачи с Украины.
а когда счет стал 4:1 ?
После нормально проведенного SRM'а.
А почему Вы не увеличиваете счет КФа, после удачно проведенного раунда?
я думал, ты по фейлам только считаешь :)
вообще-то любой однозначно понимаемое слово и оно может обозначать только "совершенно любой из множества, выбранный произвольно", таким образом из множества женихов может при проверке быть выбран совершенно любой, а следовательно богаче нужно быть каждого из них. Ты путаешь слово любой со словами "один из". Если бы там было написано "более богатого, чем один из предыдущих", тогда и только тогда это можно было понимать иначе. Все-таки у этого слова вполне четкое определение. И под любым всегда подразумевается не какой-то, а любой(т.е. по сути она тебя сравнит с каждым) из предыдущих. Недопонимание скорее возникает в неправльных интерпретациях фраз русского языка, а не в некорректности создателей задачи. Если филологически разбирать слово и придираться, то правы будут именно они. так-то =)
Нет, Вы здесь не правы, у слова "любой" 2 значения, сам вчера убедился, посмотрев в словаре.
блин во всех олимпиадах (в основном математике) очень часто (читай всегда) встречается слово любой в значении, которое написал _GnoM_. имхо сразу понятно, что имеется ввиду. ну и к тому же не зря же сэмплы составляют.
Mat Analiz :dlya lubogo ==dlya kagdogo
Русский язык такой русский %) Слово "любой" можно понимать ещё как математический термин (в математике "каждый" как-то не очень употребляется), тогда всё становится четко. Другой вопрос — что в задачах литературные условия, и математическая терминология может в голову не прийти. Но раз были сэмплы, позволяющие определить правильную трактовку, то по-моему как-то неправильно критиковать автора.
Ну почему же, здравая и обоснованная критика ещё никому не вредила. Другое дело, что не стоит, пожалуй, настолько перегибать палку.
кто же такую меморизацию делает, там из-за мапа логарифм вылазит.
Мне было удобнее завести массив 1010 * 1010. Но это авторское решение, которое должно быть неоптимально, дабы более медленные решения тоже проходили. Возможно поэтому мап.
задача D:
Вроде бы понятно, но не хватает знаний по теории вероятностей, отсюда возникают вопросы. Может у вас есть какая нибудь статья на эту тему? Сам искал, но кроме условной вероятности, найти что-то полезное не получилось. Спасибо.
Мое решение было абсолютно тупым, не основывающемся на таком наблюдении, что выпрыгивания можно игнорировать. Я считал вероятность выигрыша принцессы
double D(int w, int b, bool isPrincessMove)В некоторых граничных положениях, можно сразу определить исход игры. Например если ход принцессы, и нет черных мышей, то она выиграет, если белые мыши остались, и проиграет в противном случае. Если ход дракона, и белых мышей не осталось, то принцесса проигрывает. функцияV(w, b)выкидывает случайную мышь, и передаёт ход принцессе. В функции также рассмотрены граничные случаи, когда какой-либо цвет закончился.Перекрестную рекурсию сложно назвать "абсолютно тупым решением"))
Приведу тогда еще для коллекции ссылку на свое нерекурсивное решение
ну а куда тупее то? можно как ты, разобрать случаи с вылетанием мышки, но это куда более нетривиально, чем просто выкинуть одну случайную мышку:
x * D(x - 1, y) + y * D(x, y - 1)Есть решение D за O(W+E): Для начала заметим, что на то, что мышки выпрыгивают можно не обращать внимания. Интуитивно понятно: мышки выпрыгивают равновероятно, игроки вытаскивают мышей равновероятно. Строго доказать не могу, т.к. не хватает знаний теорвера. Тогда достаточно проитерировать по ходам поддерживая вероятность того, что игра закончилась на каком-то из предыдущих ходов и вероятность того, что принцесса выиграла после какого-то из предыдущих ходов. Тогда вероятность того, что принцесса выиграет в текущем раунде равна 0, если ходит дракон и pw = w / (w + b - i), где i — номер текущего хода, если ходит принцесса. Вероятность того, что игра закончится на этом ходу равна pEnd = w / (w + b - i), вне зависимости от того, чей сейчас ход. Тогда к общей вероятности победы нужно добавить pw(1-probOut), где probOut — вероятность окончания игры на каком-то из предыдущих ходов, а к probOut нужно добавить pEnd * (1 - probOut). Ещё на каждой итерации будем считать количество вытянутых/выпрыгнувших кроликов, во время хода дракона его нужно увеличивать на два, а во время хода принцессы на один. Понятно, что итерировать нужно до тех пор, пока количество кроликов, которые были вытянуты или выпрыгнули, меньше, чем суммарное количество кроликов. В итоге получаем вот такой код, который получает АС: 1140489
Классное решение, спасибо)
Гениально!
Спасибо. Кто-нибудь знает доказательство того, что выпрыгивания можно игнорировать?
Все-таки, хотелось бы вернуться к обсуждению задачи В. Как ее решать в целых числах, я уже понял (требует длинки и расчетов в дробях). Вопрос в том, что автор явно предполагал нецелочисленное решение этой задачи. Например, есть замечательный тест
1 77 5 3 72И его нет в тестсете. Этот тест замечателен тем, что в нем драгоценность бросается ближе всего к замку (среди всех возможных тестов), и расстояние до замка в этот момент порядка 3 * 10 - 7. Он показывает, что eps сравнения должен быть 10 - 7 или меньше (кстати, этот тест валит некоторые АС-решения). Есть еще замечательный тест
18 72 1 3 112На котором по неизвестной мне причине валятся MS VCPP решения без eps (по крайней мере, 2 или 3 АС-решения с одной страницы его не выдерживают).
Казалось бы, понятно, всего не предусмотришь. Вопрос лишь в том, как можно доказать корректность нецелочисленного решения и не получить эти тесты? Вот если ограничения были бы чуть больше (скорости до 1000), то был бы тест (не уверен, что худший)
1 707 10 6 115и в этом тесте блестящий предмет бросается чуть больше, чем за 10 - 9, а это 12ый порядок сравнения с возможными вытекающими ошибками в обратную сторону.
Просто пожелание на будущее — будьте аккуратнее с нецелочисленными задачами.
Этим меня очень раздражали задачи на геометрию в свое время. Гадание эпсилона в авторском решении, long double и использование разных эпсилонов в различных ситуациях в одном и том же решении. Бесит. Действительно, зачем делать такие ограничения, что существуют тесты, которые валят точность обычного double? Мне это непонятно. Помню что в какой-то задаче, расстояние было порядка 1e-11. Или другой пример, когда команда USTU Frogs написали формулу как-то не так, как пишут её обычно, и получили ошибку при сложении/вычитании очень маленьких значений, это какая-то известная бага/фича даблов, возникающая если не ошибаюсь из-за "нормализации". Короче черт ногу сломит в дебрях устройства double, и думаю не цель каждого олимпиадника до деталей знать тонкости его работы. Короче ИМХО делать задачи с даблами, нужно всегда очень осторожно, и следить чтобы они не превращались в задачи на длинку.
По поводу аккуратности с задачами на нецелочисленную арифметику — в авторском решении D вызывает некоторое сомнение "if (cont_prob > 1e-13)" без анализа количества вызовов функции и как это повлияет на конечный результат. Должна быть некоторая уверенность, что результат будет получен с точностью 1e-9. А так, эпсилоны от фонаря уже стали некоторой традицией в олимпиадной программировании. :)
Задача D — вообще отдельная история. Я надеюсь, у авторов было точное решение, поскольку есть много нехороших примеров, когда в даблах расчеты просто неверны. Обычно везет, но — например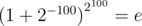
, при этом 
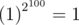, и это всего 100 операций вида x: = x2.
Upd. Хотя динамики, подобные этой, вроде всегда вычислительно устойчивы.
Кстати, \leftarrow в TeX не работает.
"Количество чисел от 1 до D, кратных T, равно (D — 1) / T."
Откуда -1?
Да, действительно. Типичная off-by-one error. Спасибо :-)
In problem B,most solutions use double to calculate the distance between the princess and the cave...but I think the precision of double may lead sth wrong... I think it is not a good way to use the double...for example,you may get a distance of 9.99999999999999,but indeed it means 10. and if the distance between the castle and the cave is 10, these solutions will give the wrong answer that one more bijou than really needed..
I tried to solve it by using rational arithmetic library of my own in C++, with both numerators and denominators of type
long long. It seems the test cases included the one that deliberately tried to overflow numerators and denominators. So you need arbitrary-precision arithmetic to solve this w/o floating-point numbers, which is a bit hard in C++.= =I know. But as a problem writer, it's not fair to prepare no data to fail the implementation using double.Because a careful participant may use something safe but more complicated(such as rational,java.math.BigDecimal) to implementation, and it takes more time which means lower score. Moreover,to accept a likely wrong solution is itself ironic.
If you guys disagree with me,please tell me why...
I agree with you in general case, but for this problem, bruteforce says: the worst possible test case is 17 99 1 3 999 minimum difference between current path and C is 0.00000047198966512951
It seem's like the solution of pE has the complexity of O(N^4) for enumerate N shelves and for each shelf there could be 100(N) items and for every time you advance to the next shelf you should calculate all the M possibilties...
so let's assume that val(i, j) means the maximum value when you take j items at the i-shelf and DP(i, j) means the maximum total value we took from the (1~i)-shelves when we had took j items where DP(i,j)=max(DP(i-1,j-k)+val[i][k]), but we'll have to enumerate k from 0~100
which part have I mistaken? shouldn't the complexity be O(100^4)? Or is there something wrong in my solution?
You solution is right and the complexity is really O(100^4).
Then how can a solution of this large complexity pass in < 0.25 Second?
Do you have any ideas?
148A - Insomnia cure I write a solution for problem A by the technique you mentioned second but can't get the correct output. What am I missing :/ http://ideone.com/fS5eup#
For Solving Insomnia Cure Problem using the inclusion-exclusion principle:
Let's imagine a simpler case in which "Every k-th dragon got punched in the face with a frying pan. Every l-th dragon got his tail shut into the balcony door." so every m-th and n-th dragon go away safe. In this case how to calculate the number of damaged dragons ? - every kth dragon, there is definitely: d/k dragons damaged - every lth dragon, there is definitely: d/l dragons damaged - but some of the dragons damaged were counted twice, i.e., the same dragon got punched and go his tail shut into the door, so we must subtract them by the principle: the principle says to get the union set size ,you need to subtract the intersection size from the size of the two sets. - but what is the intersection set? set of number that can be divided by k and also by l, definitely any multiple of k*l is qualified but are these numbers only the numbers in the set ? no, in fact multiples of least common multiple of k and l satisfy the requirement, i.e, lcm (k,l). To get the size of this set in the range till d, calculate: d/lcm(k,l) Now what to do for a harder case of more m-th and n-th dragon getting damaged? use the generalization of the equation above :
Thanks for this. I was having the same problem. I guess I wasn't getting the right answer because I was using plain multiplication instead of LCM.
now i have same problem with you
148E Porcelain's time constraint is too tight for python (100^4 complexity). Also I think that partly explains the low # of solved submission. (I know this is 6 years back ... but still feel unhappy when TLE due to language)
In F we can precalculate the max cost for each shelf for each size greedly using prefix sum my solution