160A - Twins
В этой задаче требовалось найти подмножество наименьшего размера, сумма чисел в котором строго больше, чем половина суммы всех чисел. Несложно понять, что выгоднее брать наибольшие числа в массиве, так мы быстрее наберем нужную сумму. Тогда решение выглядит следующим образом: отсортируем числа по невозрастанию и переберем сколько первых чисел заберем мы, а сколько – наш близнец, Как только у нас строго больше, чем осталось для близнеца – выведем ответ.
160B - Unlucky Ticket
Запишем в массив a первые n цифр, а в массив b — последние n цифр, и отсортируем эти массивы. Нетрудно понять, что если для всех i выполняется a[i] < b[i], или для всех i выполняется a[i] > b[i], то билет точно является несчастливым. Но также нетрудно понять, что для любого несчастливого билета выполняется или первое условие, или второе. Таким образом, мы придумали критерий несчастливости, можно реализовать за время O(n·log(n)).
160C - Find Pair
Для начала, мы, авторы раунда, хотим отметить, что эта задача вызвала множество вопросов, хотя в условии было совершенно четко и недвусмысленно написано, что нужно делать. Более того, на почти все вопросы по условию этой задачи мы отвечали скопированным из текста предложением – и у большинства участников больше вопросов не возникало.
Пусть число k и массив a заданы в 0-нумерации, а сам массив отсортируем. Тогда если все числа различны, то очевидный ответ – это пара (a[k / n], a[k % n]), где операция % означает остаток по модулю. Однако, если в массиве есть повторяющиеся числа, то ситуация становится немного хитрее, рассмотрим пример: пусть дан массив (1, 1, 2, 2), тогда пары записаны следующим образом: (1, 1), (1, 1), (1, 1), (1, 1), (1, 2), (1, 2), (1, 2), (1, 2), (2, 1), (2, 1), (2, 1), (2, 1), (2, 2), (2, 2), (2, 2), (2, 2), каждая пара учитывается и никуда не девается, всегда рассматриваются ровно n2 пар чисел.
По-прежнему верно, что первое число – это a[k / n]. А второе число – это a[(k–n·cnt) / num], где cnt – количество чисел в массиве строго меньших, чем a[k / n], а num – количество чисел в массиве, которые равны a[k / n].
В этой формуле несложно убедиться, рассмотрев пару примеров с повторяющимися элементами. В крайнем случае, можно написать тривиальное решение за O(n2·log(n)) и убедиться, что вы правильно придумали формулу.
P. S. Претест 3 имеет вид: в массиве (1, 1, 2) нужно найти 3-ю по лексикографичности пару. Она равна (1, 1).
160D - Edges in MST
Во-первых, разберем случай, когда все веса одинаковы. Тогда очевидно, что любое ребро может быть в дереве, но в случае, если ребро – мост, то оно является единственным способом соединить две компоненты, а значит, оно принадлежит любому MST. Итак, для мостов ответ равен «any», а для всех остальных – «at least one».
Рассмотрим алгоритм Краскала (или Крускала – кто как привык). В нем в MST пытаются добавляться ребра в порядке возрастания их весов. Но если у двух ребер вес одинаковый, то их порядок добавления может быть любым, а значит, одно ребро может зависить от того, добавилось раньше другое ребро того же веса, или оно добавится позже.
А значит, мы можем решать задачу по слоям: на каждом слое мы рассматриваем одновременно все ребра с данным весом, а сами слои – в порядке возрастания веса.
Построим на каждом слое отдельный граф, причем вершинами будут являться уже сформированные на данный момент компоненты связности, а ребра добавляются между соответствующими компонентами. Если ребро – петля, то значит, что существует способ связать два конца этого ребра за меньшую стоимость, и это ребро никогда нам не нужно, ответ для него – «none».
Если ребро в построенном графе – мост, то по ранее разобранному случаю, ответ для него «any», а для всех остальных – ответ «at least one». При разборе этих случаев нужно быть аккуратным, потому что при сжатии графа появляются мультиребра, ответ для них всегда «at least one», потому что ни одно из повторяющихся ребер не является мостом.
Решение это задачи можно реализовать за время O(n·log(n)).
160E - Buses and People
Для начала, промасштабируем все координаты и времена, а также, так как все ti различны, то запомним для каждого ti номер автобуса, который поедет с этим временем.
Для каждого автобуса создадим событие вида «при координате si появляется автобус, который поедет в момент времени ti и уедет до точки fi». Для каждого человека создадим событие вида «при координате li появляется человек, который поедет в момент времени bi и уедет до точки $r_i$».
Эти события отсортируем в порядке возрастания координаты (si, если это автобус, и li, если это человек) и будем выполнять в этом порядке.
Будем поддерживать структуру данных, в которой для каждого времени ti будем хранить максимальное fi автобуса, который едет в этот момент. Тогда если текущее событие означает автобус, то нужно просто обновить соответствующее значение в структуре данных. А если текущее событие означает человека, который в момент времени bi поедет до остановки ri, то нужно с помощью структуры данных отвечать на запрос «найти в структуре минимальную позицию t, которая не менее bi, а соответствующее ему значение не менее ri», тогда соответствующий этому t номер автобуса и есть ответ.
Вопрос в том, какую структуру данных использовать. Проще всего это делать с помощью дерева отрезков по максимуму, тогда на этот запрос можно отвечать за время O(log(n)), но также можно было использовать и другие структуры данных, например декартово дерево с неявным ключом и др.
Таким образом авторское решение работает за время O((n + m)·log(n + m)).
Существует достаточно простое решение с двумерным деревом отрезков, работающее за O((n + m)·log2(n + m)), но не гарантировалось, что оно уложится в Time Limit.











Спасибо за разбор — оперативно :) 3-я задача понравилась. Хоть и не уверен, что все тесты у меня по ней пройдет, но подковырка интереснейшая :) Ждем 4-ю и 5-ю.
Удалил комментарий. Глупость признаю.
Да и по времени не катит... 10 в 5 степени еще и в квадрате в худшем случае...
Помимо того, что не должно работать по времени (O(n^2) при N до 100000).
Не работает в случае когда в массиве будут одинаковые элементы, например при массиве: 1 2 2
Должен получиться порядок: (1,1) (1,2) (1,2) (2,1) (2,**1**) (2,2) (2,**2**) (2,2) (2,2)
В Вашем решении получится: (1,1) (1,2) (1,2) (2,1) (2,**2**) (2,2) (2,**1**) (2,2) (2,2)
Как делать правильно — написано в разборе.
Если я не ошибаюсь, то индексы должны быть k/n и k%n, а не наоборот
пусть дан массив (1, 1, 2, 2), тогда пары записаны следующим образом: (1, 1), (1, 1), (1, 1), (1, 1), (1, 2), (1, 2), (1, 2), (1, 2), (2, 2), (2, 2), (2, 2), (2, 2), каждая пара учитывается и никуда не девается, всегда рассматриваются ровно n2 пар чисел.
42 = 12?
В посте 16 нарисовано... странно.
поправил автор потому что :)
Потому что писалось в темпе и не очень внимательно. Я поправил, спасибо
В последних раундах С — задача с подвохом :) И здесь походу не обошлось :)
уже не первый раз вижу разбор задачи(сейчас это Д), где надо научится решать задачу для ребер одинаковых весов, а потом уже это обобщить на слои. На ОнлайнЖаджах есть еще такие задачи?
"Упрости задачу и увидишь суть в ней" — один из базовых принципов при решении сложных задач. Эта задача у меня, например, "щелкнула", т.е. правильное решение я просто понял сразу. Не знаю, была ли она где-то или я уже об этом думал когда-то. Если задача не "щелкает" сразу, есть несколько подходов, например, снять с задачи "отпечатки пальцев" — родственные этой задаче алгоритмы и идеи. В этой задаче это, очевидно, MST и поиск мостов.
К чему это я все? К тому, что бессмысленно искать на джаджах задачи на массивы. Или на использование сортировки. Каждая четвертая задача может быть решена при помощи этого принципа.
Пример. Задача Е этого же контеста. Будем считать, что отрезки перемещения автобусов и пассажиров имеют длину 1. Совершенно очевидно, что можно просто эмулировать процесс при помощи set-а. Будем считать, что только перемещение пассажиров имеет длину 1. Та же эмуляция сохраняется за счет амортизации запросов. Остается только научиться вместо пассажира с отрезком длины 1 находить произвольного пассажира, который доедет этим автобусом. Это запрос пары с поэлементным сравнением с другой парой, обычно он может быть выполнен, если по одной из координат построить дерево отрезков.
Я почему-то надеялся, что поиск мостов в D — из пушки по воробьям.
Удалил коментарий из-за своей глупости
И что?
2 — 1
4 — 2
В задаче D такая же идея была, но я с С парился и не смог ее решить)) P.S: codeforces работает заметно быстрее чем раньше, это радует
Мне кажется, что в разборе задачи C есть неточность. Если массив пар и массив числе нумеруются с нуля, то ваше решение не пройдет первый семпл. 2 4 2 1. k = 4, значит первое число мы должны взять из ячейки k/n = 2, но ячейки 2 не существует.
Скорее всего там надо (k-1)/n и во втором числе тоже надо изменить формулу (k-n*cnt-1)/num.
Вот решение, с измененными формулами 1307453
Число k тоже считается от 0. Вот решение в 0-нумерации 1295824
Ясно, извините, неправильно прочитал.
Интересный был тур особенно 3-я задача
На самом деле в Е можно обойтись без деревьев отрезков: можно делать почти то же, что описал автор, только на каждом промежутке размера (корень из Н).
Для этого надо посортировать маршруты по Т. После этого мы на каждом этапе выделяем все запросы, которые могут оказаться покрытыми данными корень из Н маршурутами. То есть мы забиваем на время, и просто проверяем, есть ли среди данных нам маршрутов такой, который покрывает наш запрос полностью (делаем это просто с помощью сортировки событий и запроса "активный маршрут с максимальной позицией конца"), и при этом он начинается не позже последнего из текущих корень из Н маршрутов. Запихиваем все возможные события в массивчик и проверяем, подходят ли они нам еще и по времени, втупую, за количество возможных запросов * корень из Н.
Почему это нормально работает? Мы добавим запрос в массив возможных "ложно" не более одного раза, это произойдет только если наш запрос покрывается, но маршрутом, который возник раньше его. А так как маршруты отсортированны по времени, такое произойдет максимум 1 раз, в следующий раз если мы добавим запрос, то он точно кем-то покрыт.
Более того, в таком случае можно наш сет заменить просто на стек и просто проходить события как открывающие — закрывающие скобки. Если на вершине стека промежуток с концом дальше текущего запроса, то запихиваем текущий запрос в массив, иначе выбрасываем его с верхушки стека. Правда, о ценку это не меняет —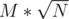 , если я нигде не просчитался. Ну и даже с сетом вместо стека заходит за 880мс.
, если я нигде не просчитался. Ну и даже с сетом вместо стека заходит за 880мс.
UPD: Просчитался, меняет, с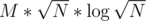 до просто
до просто 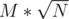
--тут было что то глупое--
"Например, билет 2421 удовлетворяет данному критерию несчастливости и счастливым являться не будет (искомое соответствие 2 > 1 и 4 > 2)"
Задача C. На дорешивании написал решение как в разборе, но получаю RE 28. Сделать дебаг теста не получается, так как там числа очень большие. Что может быть? Посмотрите пожалуйста...
мне кажется, что у вас num — это количество элементов меньше или равных a[k / n], а должно быть просто равных.
Да вроде бы нет.
if (a[i] < a[x]) continue;Вопрос снят, спасибо. Дело было в несоответствии типов, видимо в этом месте
a[(k - n*cnt) / num]. Получалось кривое значение и соответственно RE (выход за границу вектора). Переопределил n, k, cnt и num как int64 и прошло :)Попробуйте
x,cntиnumсделатьint64.P.S. опоздал :)
В таких случаях можно сгенерировать большой корректный тест самому.
А как при решении задачи D может быть использован алгоритм Тарьяна? Видел его у многих авторов.
Пардон, немного не пойму решение D. Если веса всех ребер разные, получается n слоев, поиск мостов работает за O(n + m), а так как в этом слое одно ребро, то и вовсе за O(n), и получается, что при проходе n слоев, в каждом из которых ищутся мосты тратится время O(n^2). Скажите, где я ошибаюсь.
Обход в глубину можно реализовать за M, если не запускаться из изолированных вершин.
Ок, спасибо, будем пробовать
Поиск мостов запускается только по рёбрам на данном слое.
P.S. да что же я так медленно пишу)