651A - Джойстики
Автор идеи: fcspartakm, разработчик: fcspartakm.
Главной идеей решения является то, что в каждый момент времени нам нужно заряжать джойстик с самым низким уровнем заряда. По-этому мы можем просто проэмулировать процесс или вывести простую формулу за O(1).
651B - Красота картин
Автор идеи: fcspartakm, разработчик: fcspartakm.
Давайте посмотрим на ответ, в нем будет несколько подряд идущих отрезков возрастания красоты, а между ними красота будет падать. Будем решать задачу жадно: давайте отсортируем массив значений и будем набирать возрастающие куски по очереди. Чтобы набрать очередной кусок мы идем слева-направо и среди каждого множества картин с одинаковым значением мы выберем только одно. Так будем продолжать пока картины не закончатся.
Если аккуратно это реализовать, то получим решение за  .
.
Но такое решение дает нам всю последовательность, но в задаче от нас по-сути просили вычислить только число отрезков возрастания. Из прошлого решения следует, что мы наберем столько отрезков возрастания, сколько максимум раз повторяется в массиве одно из наших чисел. Очевидно, что мы не можем набрать меньше. Получаем решение за O(n).
651C - Хранители/650A - Хранители
Автор идеи: ipavlov, разработчик: ipavlov.
Когда манхетенское расстояние совпадает с евклидовым?
deu2 = (x1 - x2)2 + (y1 - y2)2
dmh2 = (|x1 - x2| + |y1 - y2|)2 = (x1 - x2)2 + 2|x1 - x2||y1 - y2| + (y1 - y2)2
Это означает, что они равны только когда x1 = x2 или y1 = y2. Что посчитать ответ нам нужно выяснить, сколько точек лежат на каждой горизонтальной и на каждой вертикальной прямой. Это легко сделать с помощью std::map/TreeMap/HashMap/Dictionary, или если просто отсортировать координаты.
Если у нас есть k точек на одной горизонтальной или вертикальной прямой, то они добавят в ответ k(k - 1) / 2 пар. Но таким образом мы дважды посчитаем пары совпадающих точек, то есть нужно будет вычесть из ответа посчитанные таким же способом числа пар одинаковых точек.
Если мы воспользовались TreeMap/sort, то мы получим решение за  , а если unordered_map/HashMap, то O(n).
, а если unordered_map/HashMap, то O(n).
651D - Просмотр фотографий/650B - Просмотр фотографий
Автор идеи: fcspartakm, разработчик: fcspartakm.
Какие фотографии мы увидим в конце? Сколько-то от начала и возможно сколько-то с конца. Всего есть 4 случая:
- Мы всегда двигались только вправо.
- Мы всегда двигались только налево.
- Сначала мы двигались направо, потом сменили направление движения, прошли все просмотренные фото и продолжили движение налево.
- Сначала мы двигались налево, потом сменили направление движения, прошли все просмотренные фото и продолжили движение направо.
Первые два случая делаются банально, просто эмулируем. Третий и четвертый случай можно решить с помощью метода двух указателей. Заметим, что если мы пройдем в третем случае на одну картину больше справа, то мы потратим больше времени и число просмотренных фото слева уменьшится. Так двигаем эти два указателя и пересчитываем текущее время.
Это решение работает за O(n).
Альтернативным решением является зафиксировать сколько мы пройдем справа, а потом найти сколько мы пройдем слева с помощью бинарного поиска. Для этого нам нужно будет предподсчитать для каждой позиции слева и справа, сколько времени мы потратим, дойдя до нее.
Это работает за  , что немного дольше, но возможно кому-то так проще было решать.
, что немного дольше, но возможно кому-то так проще было решать.
651E - Сжатие таблицы/650C - Сжатие таблицы
Автор идеи: LHiC, разработчик: iskhakovt.
Сначала решим задачу, когда все значения различны. Мы построим граф, где вершинами будут являться ячейки таблицы, а ребра будут вести из одной ячейки в другую, если у первой значение меньше, чем у второй и они лежат в одной строке или в одном столбце. В этом графе нет циклов, так что мы можем вычислить сжатые номера ответа с помощью динамического программирования:
for ( (u, v) : Edges) {
dp[v] = max(dp[v], dp[u] + 1);
}
Мы можем это сделать с помощью топологической сортировки или ленивых вычислений.
Если мы построим граф как описано, то в нем будет O(nm(n + m)) ребер. Чтобы уменьшить это число мы отсортируем каждую строку и каждый столбец и добавим ребра только между соседями в этом порядке. Тепеть у нас O(nm) ребер, которые мы вычисляем за время 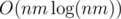 .
.
Теперь вспомним про одинаковые значения. Давайте построим точно так же второй граф, но теперь в нем ребра будут означать равенство. Теперь если мы найдем компоненты связности в этом графе, они и будут являться вершинами нашего нового первого графа.
650D - Канатная дорога
Автор идеи: LHiC, разработчик: LHiC.
Нам нужно вычислять длину наибольшей возрастающей подпоследовательности (НВП) после каждого из независимых изменений к массиву.
Для начала вычислим длину НВП в нашем исходном массиве и обозначим её за k. Пока мы это вычисляем, нам понадобится хранить дополнительную информацию lenl[i] — максимальную длину НВП, заканчивающуюся на данном элементе. Аналогично нам понадобится lenr[i] — максимальная длина НВП, начинающейся с данного элемента (мы можем это вычислить аналогично, только нужно будет идти по массиву в обратную сторону).
Давайте решим тот случай, когда наш новый элемент будет лежать в новой НВП. Длина максимальной НВП, проходящей через эту точку будет равна maxi < a, h[i] < b(lenl[i]) + 1 + maxj > a, h[j] > b(lenr[j]). Это можно вычислить онлайн с помощью персистентного дерева отрезков или оффлайн с помощью обычного дерева отрезков и метода сканирующей прямой, что будет работать за  на запрос. Это единственный случай, когда ответ будет больше k, точнее он может быть только k + 1.
на запрос. Это единственный случай, когда ответ будет больше k, точнее он может быть только k + 1.
Во втором случае, когда наш элемент не входит в ответ, но то что мы его поменяли привело к порче всех исходных НВП, то ответ будет k - 1. Иначе у нас останется хотя бы одна НВП длины k, она и будет ответом.
Как это понять? Давайте посчитаем число НВП в исходном массиве по какому-нибудь модулю. Мы можем это сделать с помощью динамического программирования также, как мы искали саму НВП, например с помощью дерева отрезков. Тогда мы можем проверить, если liscount = liscountleft[a] * liscountright[a], то это как раз означает, что все НВП проходят через наш элемент.
Если вам не нравится решение с таким "хешированием", то есть алтернативный честный подход. Для каждого элемента давайте поймем, может ли он входить в какую-нибудь исходную НВП, а если может, то на какой позиции(эта позиция будет как раз равна lenl[i]). Тогда для каждой позиции мы посчитаем, сколько различных элементов претендуют на нее. Если только один элемент, то это как раз и означает, что все НВП проходят через него.
Получаем решение за  .
.
P.S. Мы можем решить эту задачу без использования структур данных с помощью альтернативного метода вычисления НВП с помощью динамического программирования и бинарного поиска.
650E - Часовой механизм
Автор идеи: Zlobober, разработчик: Zlobober.
Первое соображение: ответ всегда равен числу ребер, которые есть в первом дереве, но которых нет во втором. Это означает, что если у нас есть ребро, которое лежит в обоих деревьях, то это ребро можно удалить, а те две вершины, которые оно соединяло, объединить в одну, ничего не изменится.
Второе соображение: если мы возьмем любое ребро из первого дерева и удалим его, то всегда найдется корректное ребро из второго дерева, которое можно вставить обратно (если такого нету, то это означает, что второй граф не связен, а он дерево, противоречие). Таким образом порядок замены ребер из первого дерева может быть произвольный.
Третье соображение: если мы взяли лист в первом дереве, выкинули соответствующее ему ребро, то мы можем добавить любое ребро из второго дерева, которое ведет из данной вершины.
В итоге получаем алгоритм: храним списки ребер в вершинах, когда ребро общее, то объединяем вершины с помощью системы непересекающихся множеств, а их списки склеиваем вместе. Чтобы получить порядок ребер в первом дереве мы сделаем его обход в глубину и получим такой список, что если мы уже убрали все прошлые ребра, то следующее всегда будет листом.
Получаем асимптотику O(nα), что на практике является линейным алгоритмом.










Finally...
16609675
What does this above solution for the Div2-C run in? Is it O(nlogn) or O(n) or worse than that? I'm not able to figure out. Thanks!
nlgn because you sort the array of guards
maybe even worse than nlog n, because you have two nested for loops in the end, but I couldn't determinate what the exact complxcity...
Good contest.
There is no point in sorting an array in div2B. Number of segments with increasing beauty is just the maximal number of occurences of the same beauty (denote it by X). It cannot be less, because there is at most one painting with the most frequent beauty in each segment, and we can make it exactly X with a greedy algorithm. So we lose at least (X-1) happinesses on the borders of these segments of (N-1) possible, the answer is (N - 1) - (X - 1) = N - X, and we can get it in O(n) time.
Yes, i've described the solution for the harder problem — how to output this sequence.
Awesome. Took some time to understand well.
The idea is awesome once you understand it. Maybe a more detailed description will be better? When I was trying to follow the idea, I was confused by this test case: 100 100 100 100. Once you can figure out how this test case follows the idea described above, you will understand it.
It is always hard to determine what details to explain and what to omit (in explanation of an algorithm or mathematical proof), because different people need different degree of detalization.
romanandreev can you please give the c++ code of problem C- watchmen using TreeMap/sort
When i say A/B/C, i mean A or B or C.
Hello.
Could anyone please explain in C how we get 11 in the second output?
0 0 0 1 0 2 0 1
4*(4-1)/2 — 2 = 4
0 1 -1 1 0 1 1 1
4*(4-1)/2 — 2 = 4
4 + 4 = 8
Where am I wrong?
Hello, if I can see well, then second input is:
61) 0 02) 0 13) 0 24) -1 15) 0 16) 1 1Now, let's see.. for first point it is true while paired with points2 3 5, for second3 4 5 6for third5for fourth5 6and for fifth6(notice I have not wrote the duplicates) anyway it makes3+4+1+2+1+0==11.can anyone explain the implementation of div2-c problem??
Hello, well .. it is true for pair of points if they share x or y coordinate. So an implementation would look like to group all points, which share x/y coordinate. It can be done by two maps, which would be indexed by the coordinate. Here, for every group, the number of pairs is N*(N-1)/2. Anyway here is a little problem, that all pair points which share both x/y coordinate (so they are same) were counted twice. So you will have to create another map, indexed by the points (and every group will be substracted by similar formula [N*(N-1)/2])
Thanks for editorial! I have one issue for future editorials in general — difficulty in problems like DIV2-A and DIV2-B lies mostly in proving the greedy algorithm correctness, not in implementation, so it would be really nice if future editorials focus a little bit more on how to prove such greedy solutions. I understand writing full proof might be tiresome thing to do, but it gives a reader a really good opportunity to learn how to prove things quickly and in contest time.
I've added some explanation to the DIV2B problem. But i think tutorials should leave reader something to think about. Also some things are omitted for the sake of simplicity.
Could someone please explain Div2 E in more detail? Especially this part "But to solve the problem completely in the beginning we need to compress all equal values which are in the same rows and columns. We can construct second graph with edges between equal cells in the same way as before and find all connected components in it. They will be our new vertices for the first graph."
That is: Split the table in two graphs, first graph contains the vertices having unique value, and the second graph contains other vertices. For the second graph, add edges between same cells, and 'shrink' them(using dsu), these new vertices will be added to the first graph. Finally, we can get the min value of each cell through the toposort on the first graph.
Therefore, 3 steps in total: 'shrink' equal cells, add one-way edges, do toposort.
I think there is another solution for DIV1C with union-find sets and greedy.
Describe it, please! :D
Sort the whole array and then iterate it from smaller to larger. Maintain the maximum value of every row and column to decide what the next value will be.
I tried using this method only, but we have to take care that if a number occurs multiple times in a row or a column, then its final value should also be same. And a number x if it occurs multiple times but in different row and column then its final value needn't be same. How to handle this?
Use union-find sets to merge the sets of every "relevant" element, whose values should be the same. For every set you iterate all its members and get the maximum of their rows and columns.
prateek_jhunjhunwala The way to handle the case of equal values would be to make use of Disjoint set data structure to make sure that all the equal values which need to be SAME are put together in a single set.
You can read this here 18008861.
From lines 33 to 45 you can see the application of disjoint set to put equal values together. And in line 44
f[r2] = max(f[r1],max(f[r2],max(ax[a[k].x],ay[a[k].y])) ) ;
You can see that the parent has the best possible value that needs to be set for all the EQUAL values in this set. Finally in line 48
ans[a[k].id] = max( f[find(a[k].x) ] , f[find(a[k].y) ] ) +1 ;
We set the answer.
We had such solution as main, but i've decided to describe another one, because it contains more general ideas.
Why 651E's time complexity is O(NM log(NM)) instead of O(NM(log M+log N))? I wonder if there are mistakes during my analysis. http://codingsimplifylife.blogspot.tw/2016/03/codeforces-651etable-compression.html
Don't worry, you're ok. There's a logarithm property that says:
log(a*b) = log(a) + log(b)
So, NM log(NM) = NM(log(N)+log(M))
;D
Wow, I got it!
Thanks for your explanation!
:D
(Did I ask a stupid question? Why my comment vote became so negative...)
I guess that they thought that you should know that. But we are humans :D
в задаче Div2E
не очень понятно, что нужно делать со вторым деревом.То есть,если бы у нас были бы только различные значения, мы бы просто поднялись по топологической сортировке. А как нужно учитывать компоненты связности? понятно что у всех элементов компоненты связности, значения должны быть одинаковы
Нашел ответ на свой вопрос здесь
I have thought over it for hours still not able to find the testcase I am failing. http://mirror.codeforces.com/contest/651/problem/D http://mirror.codeforces.com/contest/651/submission/16641326
You can temporary fix that test (only temporary!) Something like
if(result == 74815) result++
So you'll pass that test (but maybe your code have another bug in the next test cases). But you need to fix that bug anyways.
This algorithm is amazing; it can solve any Codeforces problem in O(#testcases) time by reducing it to 100 if statements!
I feel a small testcase can always tell me where my algorithm is going wrong. Anyways thanks for the help.
Yes, that's right. But if you are in hurry, is a simple fix.
Just in case you still need it, here is a small test case your code fails on: 5 1 100 7 hhhhw Correct answer is 4 but your code prints 2.
Could you please explain why following test case gives 7 as answer???
10 2 3 32 hhwwhwhwwh
considering 1-indexed, shouldn't answer be 8 (1-2 && 5-10) with time 31. Need help.
Thnx
По задаче E.
Там надо склеивать 2 списка при merge в СНМ-е. Окей. Надо приливать меньшее к большему и будет работать за N log.(Или вы умеете доказывать что это быстрее?)
Я отправил решение которое просто мержит(за сумарную длинну) и оно тоже прошло.
Это нормально?
Склеивать два списка можно за O(1), что и происходит в описанном решении.
Какой id посылки, где вы склеиваете за суммарную длину?
Черт действительно можно за 1 ;) Спасибо.
А с посылкой я накосячил. За суммарную длину не проходит. Прошу прощения.
Can someone explain more about div 1 D? What does scanline mean?? I dont undrestand the approach explained in the editorial :/
In this case scanline means that we have 2D points (a, b) and we are going through them from left to right (scanning by x axis) and storing segment tree on the y-values (y-axis line).
Я решил Div.1С следующим образом:
Таким образом я получаю сложность: O(nm·log(nm) + nm·α(nm) + nm) = O(nm·log(nm))
http://mirror.codeforces.com/contest/650/submission/16608895
В задаче div. 1 D можно ещё использовать такой честный метод:
Храним три дерева отрезков. Одно для префикса i - 1, второе для суффикса i + 1. Третье — для нахождения длины наибольшей НВП без элемента i. Вначале заполним второе дерево отрезков до предела и запомним, какие изменения мы совершали. Теперь идём слева направо по позициям i, одновременно отвечая на запросы. Первое дерево обновляется очевидным образом, второе — откатом. Наконец, в третьем дереве храним в вершине число самой длинной возрастающей последовательности такой, что переход от префиксной части к суффиксной происходит в её подотрезке. Тогда lis[3][v] = max(lis[3][left], lis[3][right], lis[0][left] + lis[1][right]). Эту величину можно пересчитывать одновременно с изменением первого или второго дерева отрезков. Так мы получим lis[3][root] — наибольшая длина возрастающей подпоследовательности без элемента i.
На всякий случай lis[0][v] — наибольшая возрастающая подпоследовательность из префикса, у которой последний элемент по величине лежит в отрезке вершины v. Аналогично для lis[1][v] — наибольшая возрастающая подпоследовательность из суффикса, первый элемент которой лежит в подотрезке вершины v.
А можно подробнее о том, как решать задачу динамическим программированием?
Решение: 16576702
Мы храним dp[len] — величину минимального элемента, на который может заканчиваться последовательность длины len. Значения в этом массиве возрастают. При добавлении нового элемента все что нам нужно сделать — найти бинпоиском этот элемент и обновить значение dp.
Здравстуйте! Обьясните мне пожалуйста почему в задаче 651C — Хранители/650A — Хранители мы отнимаем только количество одинаковых точек, а не их вклад в общий ответ? Как я понимаю таким образом мы отнимаем только те пары, между которыми расстояние равно 0.
Hello! Please, explain to me why in problem 651C — Хранители/650A — Хранители we subtract only number of similar points, not their contribution to the total answer? As I understand doing this we subtract only point pairs which have distance 0.
Hello. Well if we wouldn't do it, we would get all pairs which share x coordinate + all pairs which share y coordinate. As you can see from the "statement" we clearly counted every pair, which shared both ( x and y) coordinates twice [once because they share x + once because they share y ]. So here we just substract only the pairs, we counted twice :) (which are all pairs, which are same).
Thanks a lot!
for Div1 E, i have a solution which requires union-find-delete DS implementation which i dont know how to implement. does any one has a solution which does not requires union-find-delete implementation ?
Described solution doesn't need delete operation. Read it more carefully.
In problem 651D suppose we want to find maximum number of photos we can see if we first travel right and then travel left.so basically how to know at which index we should stop when we first go right
We go through all right positions and for each one of them we identify the optimal leftmost position.
Could someone explain Div1 D(Zip line) in more detail? I don't understand exactly except the fact that answer can be k-1, k, k+1.
trying to solve div1 D with persistent segment tree
im using two persistent segment trees one to find element before and one to find element after
keep getting MLE no matter what i did
is there a way to do it with one persistent segment tree or am i missing something ?
here's the submission
For Div 1 D problem. Could someone explain me how to determine if some element belongs to all LIS?
you have to count the number of LISes that the element is the head of
and the number of LDSes the element is the head of
and if the number of the LISes in the whole array is the same as multiplying the two calculated values then the element is a part of all LISes
I got that part, but how is the algorithm to count the number of LIS?
i did it using segment tree where for each element the number of ways this element is the head of an LIS is the number of sum of ways each element before it with maximum length LIS
for example : 1 1 3 2 2 4
number of ways: :1 1 2 2 2 6
for 4 we summed ways of 3 and 2 and 2 since 3 and 2 and 2 are the head of length 2 LIS and there are no longer ones
For Div1-B problem, I used binary search to solve the problem but i am getting wrong answer for case 16. i cant figure it out, can anyone help my solution: http://www.codeforces.com/contest/650/submission/16875724
Can anyone explain the approach for Div2 E ?
Didn't get it from the editorial !
How to solve 651A in O(1)?
Can someone give the O(1) solution for Problem A — Joysticks ?
Can someone explain the solution of 651D/650B,
I dont get the tutorial solution... Why do we have to start from the 1st photo only,can't we skip the first photo and then move on the check the other ones, for example in case
5 2 4 13
wwhhw
The answer should be 3 as we can see the pictures 2,3 and 4 ("wwh"),but the algorithm given in the editorial will give answer to be "2", Maybe I dont understand the tutorial,please help,Thanks a lot!
Just realized 650C - Table Compression was revived in the ACM-ICPC 2017 Regional (Hochiminh City site, Vietnam).
Statement of the problem in the HCMC site
Ah... the nostalgia...
Thanks neko_nyaaaaaaaaaaaaaaaaa for pointing that to me...
Another non-hashing O(nlogn) solution for div1D : My submission
--------------------------------------------------------
The point is to determine whether a element in the initial array must appear in a LIS. My solution is to find the "leftmost" and "rightmost" LIS, and their intersection are the necessary elements which must appear in any LIS.
Definition on the leftmost LIS:
During the process of finding a LIS, for every element E=array[i] we have to find its predecessor P, which is the element before E in a LIS of the subsequence [1...i] containing E as its(refers to the LIS) end.Thus, if we take the leftmost P (which has the smallest index) every time, the final LIS that we get is the "leftmost" LIS.
The rightmost LIS is defined similarly.
Proof on the correctness:
Let's denote the leftmost LIS with L, and the rightmost one with R. Let P be a element in both L and R.
Obviously the index of P in L and that in R are the same. Otherwise there would be a longer increasing subsequence than L or R.
If P's predecessor in L is the same as that in R, it means there can be no other candidates for P.
On the other hand (pred_in_L(P)!=pred_in_R(P)), different predecessors lead to the same P, then it is more inevitable that P is the only candidate!
--------------------------------------------------------
Well, I know this isn't quite a scientific proof, but the solution passed all the tests after all... Waiting for a more rigorous one :)
My solution to C is completely different from the editorial. Its too long to describe too. And it just passed all cases. Here: 92662769