Собственно, задача такова:
Дан неориентированный взвешенный граф. Для каждой вершины найдите длину кратчайшего простого цикла, проходящего через данную вершину.
Быстрейшее решение, что у меня есть, работает за N^4
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
23:55:58
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
23:55:58
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 17:39:02 (i2).
Десктопная версия, переключиться на мобильную.
При поддержке
Auto comment: topic has been translated by Domonion (original revision, translated revision, compare)
are there negative edges?
seems like it's not. since it will make this problem NP-hard.
Решение за O(N3).
If O(n^3logn) is good enough, for each node, for each edge of the node, remove the edge, run dijkstras to find the distance from the node to the neighbor on the other side of the edge, and add the edge weight to it. The answer is the minimum of these.
Dijkstra's Algorithm does not run in O(N log(N)) time.
I think it's possible to do in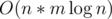
. To compute answer for vertex v, run Dijkstra from it then for every edge w suposse that this edge is included in some cycle of v in the way 
(where wA and wB are vertexes connected by edge w) and calculate its weight. Answer for v gonna be a minimum of these weights.
It's also O(n^3 log n)
No it's not. For each vertex you run dijkstra and check all edges so actually it is O(n * (m + mlogn)). Of course if there will be like n2 edges then it indeed gonna work in O(n3 * logn), but if such constraints exists then n should be quite small.
Your algorithm does not always compute simple cycles. Consider the cycle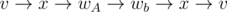
, which is not a simple cycle, but is taken into account by your algorithm.
please ignore this :(
Won't work, the graph is undirected, so A[v][v] will be 2x the lightest outgoing edge from v.
omg i was stupid. Sorry for that
I don't know if this is a coincidence or not, but it seems you are not the only one solving this problem: http://research.haifa.ac.il/~raphy/papers/all-cycles.pdf