Round 349 B Div1 : 666B - World Tour.
The Idea of problem is fixing two middle cities!
But I solved the problem by this Idea :
Consider that the answer's cities are a, b, c, d and a < b < c < d
---- dp[ k ][ i ] = the maximum length with k cities so that k'th city is i(labels are increasing!).
---- We can update dp with O(n ^ 2) [ dp[ k ][ i ] = max(j < i : dp[ k — 1 ][ j ] + d[ j ][ i ]) ]
We shuffle the labels of cities while the labels of answer's cities become increasing!
The mathematical expectation of the above algorithm is (4! * 4 * N ^ 2) :))
My implementation : 17588529.
We can have a harder problem with five cities : (5! * 5 * N ^ 2)
Very nice :)! You could have used it as a nice problem somewhere instead of just posting it here :P.
Problem has an obvious generalization for k cities. Your algorithm provides O(k!·poly(n)) complexity however we can further optimize this and use color coding technique in a very similar way as it is used in k-path problem (which suggests that further optimizations of that may be possible). We can chose one color out of k for every city and hope that every city contained in an answer got different color. If that is the case (probability of this is about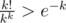
) then we can use dynamic programming on subsets of colors. dp[A][v] should be the length of longest path that contains vertices with colors from set A and ending in v (very similar as it is in Hamiltonian path). That leads to O((2e)k·poly(n)) solution.
dhawalupadhyay said that the probability of getting the desired arrangement would be 1 — (23/24)^50 ~= 0.88
And the problem has 41 test cases : 0.88 ^ 41 ~= 0.005 !!!!
It means I didn't have chance to get ACC!
But I think the test cases are weak and a random graph has a lot of answers !! what do you think about that ??