Всем привет!
Завтра в 04:00 MSK состоится личное соревнование.
Приглашаю всех поучаствовать и предлагаю обсудить задачи после контеста!
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Всем привет!
Завтра в 04:00 MSK состоится личное соревнование.
Приглашаю всех поучаствовать и предлагаю обсудить задачи после контеста!
| Название |
|---|



Is TopCoder broken? I'm getting "Your request timed out" all the time.
Any ideas for solving Div II — 1000 ?
seems like dp, but could not solve it. any ideas?
I used dp, with the following observations:
Consider the sequence of column maximum values (of a correct ordering). It is obvious that it should be a sequence of distinct numbers, and permuting them (by swapping the columns) yields a different ordering. Therefore it's sufficient to consider the sequence as non-decreasing (adding the columns from left to right), and multiplying the answer with n!.
Same as above for the rows' maximum values. With the two observations, we can safely fix number 2n - 1 on the top-left cell, and multiply the answer with 2 × n!. This also makes sure one of the columns' condition is fulfilled, and we only have to care about the other column.
We have the following dp f(i, j, k) — the number of correct ordering with i columns having at least one number, j columns having two numbers, and k — whether the second column's condition has been satisfied — calculated by adding the numbers one by one, from the largest to the smallest. Obviously f(1, 0, 0) = 1 (we put the number 2n - 1 in).
State transformation is as follow:
If i < n, we can put the next number onto the leftmost empty column.
If (j < i), we can put the next number onto a column with one number. Note any ordering of second-numbers does not affect the sequence, so f(i, j + 1, k||(nextNumber > = K)) + = f(i, j, k). You may ask why the condition check was included: Since any ordering of the second-numbers are the same, we could use a greedy approach to try creating a correct ordering, by moving the largest second-number to the second row of the first column (the one with number 2n - 1 above).
This should create a O(n2) solution, with the answer being f(n, n, 1) * 2 * n!
"the number of correct ordering with i columns having one number"
Shouldn't it be "having at least one number" ?
[Mistaken]
Yeah, but f(n, n, 1) — the number of correct ordering with n columm having one and n columm have two — it just doesn't seem right <(")
Oh.
Oh I got it.
My bad O.o.
have you considered the maximum value of the second row?
How to solve Div 1 500?
The number of possible graphs contains a directed path from u to v is 2^(N — 1 — distance(u, v)). The sum of this value for all ordered pairs (u, v) is the answer. Then we can use dfs to calculate it in O(N)
What an amazing solution!!!!
Sorry, I did not get the "dfs to calculate in O(n)" part. Could someone explain it? Thanks!
Another solution: Suppose that we choose the direction of each edge at random. We want to compute expected value of the random variable: #{directed paths}.
Let us choose a root. In each node v we remember three values:
In[v] = Expected number of nodes w in subtree of v s.t. there exists path w → v
Out[v] = Expected number of nodes w in subtree of v s.t. there exists path v → w
Ans[v] = Expected number of paths w1 - > w2 such that w1, w2 are in subtree of v and this path goes through v.
One can observe that :
One can observe that In[w] = Out[w] and
So we can compute those values in O(N) by simple dfs. The final answer is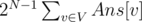 .
.
How to solve Div-1 250? If n is odd, we can choose all k numbers to be even, and that is a solution. Is there some similar way for the case when n is even? Or is this an incorrect approach?
if n % 2 ≠ 0 we can choose 2, 4, .., 2·k.
if n % 3 ≠ 0 we can choose 3, 6, .., 3·k.
if n % 4 ≠ 0 we can choose 4, 8, .., 4·k.
if n % 5 ≠ 0 we can choose 5, 10, .., 5·k.
if n = 60 we can choose 7, 14, 21, .., 98, 1.
In general for any N, you can choose a number x other than 1 such that gcd(N, x) = 1 After choosing x, you can simply generate it's multiples. However there is a corner case(s):
N being 1,
N being 60 or 90 and L = 15 which you need to take care of.