Introduction
In this post, I am going to share my little knowledge on how to solve some problems involving calculation of Sum over Subsets(SOS) using dynamic programming. Thus the name SOS DP. I have chosen this topic because it appears frequently in contests as mediu2m-hard and above problems but has very few blogs/editorials explaining the interesting DP behind it. I also have a predilection for this since I came across it for the first time in ICPC Amritapuri Regionals 2014. Since then I have created many questions based on this concept on various platforms but the number of accepted solutions always seems to be disproportionate to the lucidity of the concept. Following is a small attempt to bridge this gap 😉
Problem
I will be addressing the following problem: Given a fixed array A of 2N integers, we need to calculate ∀ x function F(x) = Sum of all A[i] such that x&i = i, i.e., i is a subset of x.
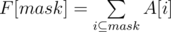
Prerequisite
- Basic Dynamic Programming
- Bitmasks
In no way this should be considered an introduction to the above topics.
Solutions
Bruteforce
for(int mask = 0;mask < (1<<N); ++mask){
for(int i = 0;i < (1<<N); ++i){
if((mask&i) == i){
F[mask] += A[i];
}
}
}
This solution is quite straightforward and inefficient with time complexity of O(4N)
Suboptimal Solution
// iterate over all the masks
for (int mask = 0; mask < (1<<n); mask++){
F[mask] = A[0];
// iterate over all the subsets of the mask
for(int i = mask; i > 0; i = (i-1) & mask){
F[mask] += A[i];
}
}
Not as trivial, this solution is more efficient with time complexity of O(3N). To calculate the time complexity of this algorithm, notice that for each mask we iterate only over its subsets. Therefore if a mask has K on bits, we do 2K iterations. Also total number of masks with K on bits is 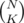 . Therefore total iterations =
. Therefore total iterations = 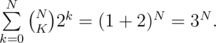
SoS Dynamic Programming solution
In this approach we will try to iterate over all subsets of mask in a smarter way. A noticeable flaw in our previous approach is that an index A[x] with x having K off bits is visited by 2K masks. Thus there is repeated recalculation.
A reason for this overhead is that we are not establishing any relation between the A[x]'s that are being used by different F[mask]'s. We must somehow add another state to these masks and make semantic groups to avoid recalculation of the group.
Denote 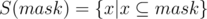 . Now we will partition this set into non intersecting groups.
. Now we will partition this set into non intersecting groups. 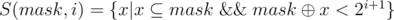 , that is set of only those subsets of mask which differ from mask only in the first i bits (zero based).
, that is set of only those subsets of mask which differ from mask only in the first i bits (zero based).
For example 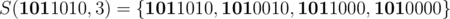 . Using this we can denote any set as a union of some non intersecting sets.
. Using this we can denote any set as a union of some non intersecting sets.
Lets try to relate these sets of numbers. S(mask, i) contains all subsets of mask which differ from it only in the first i bits.
Consider that ith bit of mask is 0. In this case no subset can differ from mask in the ith bit as it would mean that the numbers will have a 1 at ith bit where mask has a 0 which would mean that it is not a subset of mask. Thus the numbers in this set can now only differ in the first i-1 bits.  S(mask,i) = S(mask, i-1).
S(mask,i) = S(mask, i-1).
Consider that ith bit of mask is 1. Now the numbers belonging to S(mask, i) can be divided into two non intersecting sets. One containing numbers with ith bit as 1 and differing from mask in the next i-1 bits. Second containing numbers with ith bit as 0 and differing from mask⊕2i in next i-1 bits.  S(mask, i) = S(mask, i-1) ∪ S(mask⊕2i, i-1).
S(mask, i) = S(mask, i-1) ∪ S(mask⊕2i, i-1).
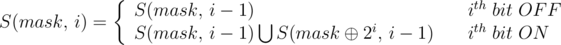
The following diagram depicts how we can relate the S(mask,i) sets on each other. Elements of any set S(mask,i) are the leaves in its subtree. The red prefixes depicts that this part of mask will be common to all its members/children while the black part of mask is allowed to differ.
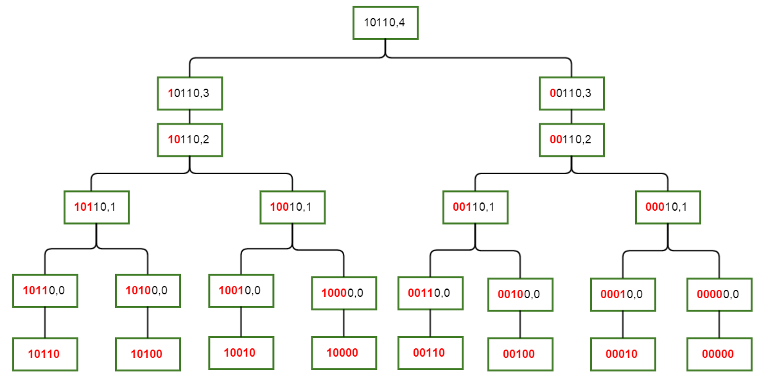
Kindly note that these relations form a directed acyclic graph and not necessarily a rooted tree (think about different values of mask and same value of i)
After realization of these relations we can easily come up with the corresponding dynamic programming.
//iterative version
for(int mask = 0; mask < (1<<N); ++mask){
dp[mask][-1] = A[mask]; //handle base case separately (leaf states)
for(int i = 0;i < N; ++i){
if(mask & (1<<i))
dp[mask][i] = dp[mask][i-1] + dp[mask^(1<<i)][i-1];
else
dp[mask][i] = dp[mask][i-1];
}
F[mask] = dp[mask][N-1];
}
//memory optimized, super easy to code.
for(int i = 0; i<(1<<N); ++i)
F[i] = A[i];
for(int i = 0;i < N; ++i) for(int mask = 0; mask < (1<<N); ++mask){
if(mask & (1<<i))
F[mask] += F[mask^(1<<i)];
}
The above algorithm runs in O(N 2N) time.
Discussion Problem
Now you know how to calculate Sum over Subsets for a fixed array A. What would happen if A and F are SOS functions of each other 😉 . Consider following modification to the problem. Assume H1, H2 to be 32 bit integer valued hash functions (just to avoid any combinatoric approach to circumvent this problem) and can be evaluated at any point in constant time.:
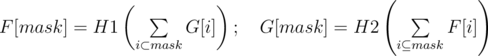
I enjoyed solving this with harshil. Lets discuss the approaches in comments :)
Practice Problems
I hope you enjoyed it. Following are some problems built on SOS.
- Special Pairs
- Compatible Numbers
- Vowels
- Covering Sets
- COCI 2011/2012 Problem KOSARE
- Vim War
- Jzzhu and Numbers
- Subset
- Jersey Number
- Beautiful Sandwich
- Pepsi Cola(resembles above discussion problem). Need to join this group.
- Uchiha and Two Products(resembles above discussion problem)
- Strange Functions(Same as above discussion problem)
- Varying Kibibits
EDIT: Practice problems are now arranged in almost increasing order of difficulty.











Great tutorial! If only I knew about this before today's contest :P
Thankyou. Did a similar problem appear in yesterday's contest ?
363 Div 1 C. You can add it to the list.
Well I don't think this technique is required to solve this problem. The dp recurrence does not demand any summation over subsets.DP for solving this problem would be
where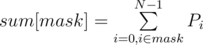
Good job!
You can also add this problem to the list: http://hsin.hr/coci/archive/2011_2012/contest6_tasks.pdf (problem KOSARE).
Thankyou. Added :)
Some more problems that use a similar approach: http://mirror.codeforces.com/contest/165/problem/E https://www.hackerrank.com/contests/countercode/challenges/subset
Thanks. Added :)
Very well written blog.
P.S:The spelling of prerequisites is wrong
Thanks. Fixed.
In suboptimal solution: What is mask initialized to ? It is this line F[mask] = A[0]
Thanks. Fixed now.
in suboptimal solution -> first for : 'i' should be 'mask'! :)
and what's value of 'i' in this line ?! dp[mask][-1] = A[i]; //handle base case separately (leaf states)
Fixed. it should have been A[mask] not A[i].
Great tutorial. I find bitmask concepts hard to undestand. But got a clear understanding with this one. Kudos to the author. :)
I think value of 'i' in 2nd last row of diagram should be zero in all case.
thanks great.
sorry, how we can prove that
for(int i = mask; i > 0; i = (i-1) & mask)will pass over all subsets ?I will give it a try. As of now I am not able to think about an easier proof. I will try to prove it by mathematical induction.
Note: Operation M-1 switches OFF the first ON bit and switches ON the remaining prefix. Eg 101100002 - 1 = 101011112
Statement P(n) = Given an integer M, this algorithm will iterate over all subsets s.t. x differs from M only in the first n bits in strictly decreasing order.
s.t. x differs from M only in the first n bits in strictly decreasing order.  algorithm successfully iterates over all elements in S(M, n) in strictly decreasing order.
algorithm successfully iterates over all elements in S(M, n) in strictly decreasing order.
Base Case P(0):
Case 1: if M is even The first iteration i = M successfully visits S(M,0) = {M}
The first iteration i = M successfully visits S(M,0) = {M}
Case 2: if M is odd First iteration i = M, second iteration i = (i-1)&M switches off the 0th bit thus visits
First iteration i = M, second iteration i = (i-1)&M switches off the 0th bit thus visits  .
.  Algo visits
Algo visits  in decreasing order
in decreasing order
Hence P(0) is true.
Assumption: Assume P(n) to be true. Algo visits S(M, n) in descending order.
Inductive step: To prove P(n+1) is true. Since P(n) is true, algo visits all S(M, n) in descending order.
P(n+1) is trivially true if n + 1th bit of M is OFF since S(M,n+1) = S(M,n).
Lets focus on case when n + 1th bit of M is ON. Since the visits of S(M,n) as assumed by P(n) are in descending order, the last integer visited by this algo would be M with first n bits OFF. For example, if M = , n = 4 the last value of i would be
, n = 4 the last value of i would be 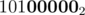 .
.
After reaching this integer, we do i = (i-1)&M. The i-1 operation turns OFF the n + 1th bit and turns ON first n bits. Taking bitwise AND with original M copies the first n bits of M into it.
Taking the example above, we have following transitions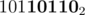 ->
-> 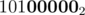 ->
-> 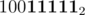 ->
->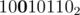 .
.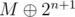 .
.
Thus what we final get is
Since P(n) is true, we can now iterate over S(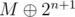 , n). But
, n). But 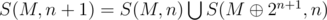 . Therefore we iterate over all elements of S(M,n+1).
. Therefore we iterate over all elements of S(M,n+1).
Hence P(n+1) is true.
The example in 2nd last line of the 2nd paragraph under heading "SoS Dynamic Programming solution" doesn't makes sense to me.
This guy 101 0000 (last element in the set) when XORed with 101 1010 will produce 1010 which is no way <= (1<<3).
Also the statement that "set of only those subsets of mask which differ from mask only in the first i bits (zero based)" conflicts with x XOR mask being <= (1<<i). It should have been x XOR mask < (1<<i). I am assuming the numbering of positions from Right to Left.
UPD : I Figured the word it all starts from 0 out !!
I have the same doubt! Is it a typo or am I missing something?
UPD: I think it should be 2^(i+1)-1.
Can we just say the following invariant:
let say j is the jth iteration then i is the jth largest value which is subset of mask
That is a great post! It really helped, thank you !!! I tryied the first problem (Special Pairs) source: http://pastebin.com/UXDiad27 But I get WA. My logic is the following: If we find 1 then because we need final result to be zero and we use AND bitwise, then we need to compare it with a number that has 0 at that position. So we go to dp[mask^(1<<i)][i-1] If we find 0 then we can have at that position 0 and 1 as well. So we are seeking in dp[mask][i-1] + dp[mask^(1<<i)][i-1]
Is the logic wrong, or just my source code ? Thanks in advance !
Got the bug.
Why man why yy yy ? And I was examining your recurrence all this time :P .It is nowhere written i!=j.
You can have a look at the diff. The correct answer was always just one less than the correct answer :P
Anyways have fun now :)
Yes! Removing that code gives AC! I thought i != j. I am sorry for your suffering checking my recurrence ! Thank you !
An easier way to solve this problem: for any A[i], to find how many numbers are there which has bitwise AND zero with A[i] -> it would just be a subset of one's complement of A[i]. So the answer is
Anyways your modified recurrence shows your proper understanding of the concept :)
Nice way! Also even if I am not so strong in bitmask I managed to think a modification because your tutorial is so clear and good that made things easier ! Thanks again !
I'm unable to understand why 2^N integers must be there in A. Is this a typo?
Actually the technique was designed for 2N integers. But you can always make an arbitrary length of array to a 2N sized array by adding extra elements with value "0".
Shouldn't it be that the number of bitmasks=2^SIZE for any integer SIZE. If SIZE itself is 2^N, then overall complexity will be SIZE*2^SIZE = 2^N * 2^( 2^N ).
N = minimum number of bits required to represent any index of the array. SIZE < 2N
Now it makes sense
great tutorial
In your memory optimized code shouldn't it be
mask is always greater than mask^(1<<i) if i'th bit is set. To calculate for i'th bit we need the value for (i-1)'th bit. In your code F[mask^(1<<i)] actually has the value for i'th bit because it was calculated for i'th bit before mask. If we start from (1<<N)-1 this won't be a problem because F[(mask^(1<<i))] will be calculated for i'th bit after the calculation of F[mask]. Please correct me if I'm wrong. Thanks :)
UPD: I just realized that for F[mask^(1<<i)] actually the calculated value for i'th bit and (i-1)'th bit is same because i'th bit is not set. So your code is correct. Sorry for ignoring it.
Thanks for informing was stuck on that !
Your comment inspired me!
if the $$$i^{th}$$$ bit of mask is $$$1$$$, then the $$$i^{th}$$$ bit of (mask $$$\bigoplus 2^i$$$) will be $$$0$$$, which will not change in this cycle!
In this case, the F[mask^(1<<i)] will remain unchanged.
So it doesn't matter which way the mask changes
Hello ,
Can you explain the formula
used in Vim War.Seems like inclusion exclusion to me but I cannot understand it.
http://mirror.codeforces.com/contest/165/problem/E Can someone explain it ? please , can't understand dp-state.
First solve this problem — Special Pairs. Then this problem should be easy. . So we have base cases
. So we have base cases 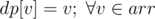 , for other masks initialize with 0.
, for other masks initialize with 0.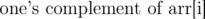 . So you can just print the number stored at
. So you can just print the number stored at  . If it is 0 then there is no solution. [ N = minimum number of bits needed to represent all the numbers of the array]
. If it is 0 then there is no solution. [ N = minimum number of bits needed to represent all the numbers of the array]
However, in my solution dp state was dp[mask] = a number from the given array such that
Now, for each array elements you need to find out another number from the array, such that their AND is 0. Note that the number you need to find will always be a subset of
My idea was almost the same. But it is getting TLE on test 12. Here's the link to my submission http://mirror.codeforces.com/contest/165/submission/29478386
Can you please check and tell me what's wrong with it?
Change cin/cout to scanf/printf! The 12th Case has 1e6 numbers, cin/cout will definitely make it TLE.
Always use scanf/printf if you have some constrains > 5e5.
Thanks a lot. I never thought that it would make much of a mess..:) I got it accepted after using scanf and printf. Thanks a lot of pointing this out.
Added a nice problem to the set. Varying Kibibits
dp[mask][-1] = A[mask]; //handle base case separately (leaf states) .
why it doesn't give array index out of bound exception
Because this is pseudocode.
Well technically, c++ doesn't check for boundaries so it should work...
But, you know, unexpected behaviour.
It's a new problem in town guys. The problem is the editorial is not explained very well ,, i guess you guys should take a look and if anyone understands may be he can shed some light for us newbies.
https://www.hackerrank.com/contests/world-codesprint-11/challenges/best-mask/editorial
It's a recent codesprint problem from hackerrank.
hey can anyone explain how to approach question this. it is similar to discuss problem but i am unable to do it? thanks in advance,
In the question explained. What is the range of x ?? And the size of array is N or 2^N ???
I can't understand this completely, maybe this is too hard for me.
What does
Fwill contain? Does accumulate ofFwill give the sum over all subsets?I want to ask that... What is the meaning of
F[mask]in the last implementation?If I need to find SoS then how should I proceed after calculation of
F?Fwon't give you sum over all subsets of the array.mask & i == i, that mean the on bits ofiis subset of the on bits ofmask.Absolutely Perfect.
Absolutely Pointless. :)
Absolutely perfectly pointless
1)
2)
What is difference between above 2 codes? Do both codes give same result?
is equivalent to first version and not the second version. The ith iteration of 1) has F[mask] = dp[mask][i]. This is not true in 2).
So 2nd version will not count some dp states. Right?
It will visit every state but t will calculate it wrong. When you do
F[mask] += F[mask^(1<<i)]. In the ith iteration forF[mask]you actually adddp[mask^(1<<i)][N-1]instead ofdp[mask^(1<<i)][i-1]. So all values are wrong.This reminds me of this: http://web.evanchen.cc/handouts/SOS_Dumbass/SOS_Dumbass.pdf
for ( x = y; x > 0; x = ( y & (x-1) ) )generates all subsets of bitmask y.
How does this iteration works? Any intuitive explaination?
x starts with the value y, and everytime you subtract 1 from x, the lowest value bit that is set would become unset, and the bits ahead of the lowest set bit (now unset) would become set.
Eg: x = y = 10100x-1 = 10011Now when you bitwise AND this with y (which was initially x), you get the common set bits between x and y ( definition of bitwise AND ).
Eg: x=10011 and y=10100x&y = 10000Everytime you AND x with y, it is making sure that x is always a subset of y.
Subtracting x by 1 after every iteration makes sure that you go through all combinations ( 2N ) of the mask y.
Further proof for the same is given by usaxena95 above.
MAXOR
MONSTER
I see it is not clear with the example above. S(1011010, 3) contains 1010000.
Let take the XOR operator: 1011010 xor 101000 = 0001010. In decimal representation, this value should be equal to 2^3 + 2^1 > 2^3, contradicting to (1011010 xor 101000)_{10} <= 2^3.
I may misunderstand. Can someone help me explain this gap?
Thanks,
Hanh Tang
Thanks for pointing that out. I have fixed that. It is now < 2i + 1.
Thank you, usaxena95.
it should be 1011010 xor 1010000 = 0001010
In this approach we will try to iterate over all subsets of mask in a smarter way. A noticeable flaw in our previous approach is that an index A[x] with x having K off bits is visited by 2^K masks. Thus there is repeated recalculationCan someone explain me this line?
The mask: 4(100) has 2 off-bits, so 2^2=4 masks will visit the mask 4(100). How?
An index x with k off bits is a subset to 2^k masks (hence it is visited by 2^k masks).
In your example case 4(100) is visited by 100,101,110,111.
Thanks
Thanks really helped alot.
Excellent editorial! Kudos...
Approach for discussion problem?
this also uses SOS DP https://www.hackerearth.com/problem/algorithm/berland-programming-contests-9c8b5165/description/ .
recent one DANYANUM
Thanks for such a nice blog
One more problem from a recent contest: Or Plus Max
can someone explain what we can't use following for(int mask = 0; mask < (1<<N); ++mask) for(int i = 0;i < N; ++i) { if(mask & (1<<i)) F[mask] += F[mask^(1<<i)]; } how to identify which one to use?
I think it's because of compiler optimizations.
can we say that when ith bit is ON then simply S(mask,i) = 2*S(mask,i-1), Because all the subsets till (i-1)th bit now have 2 choices .Either they can pair up with ith bit as 0 or 1 ??
How to solve the problem Pepsi Cola?
I think the address of dp[0][-1] is undetectable, will it go wrong?
I think the address of dp[0][-1] is undetectable, will it go wrong?
Great tutorial! Also, isn't the iterative solution akin to finding an N-dimensional prefix sum array with dimensions 2x2...x2? If this is the case, I think it could be possible to extend this idea to "bitmasks" with a different base.
Yes, see this problem.
When you do the partition, why it is a partition? Mask is in all those sets, right?
https://codingcompetitions.withgoogle.com/kickstart/round/0000000000050e02/000000000018fd5e
Jersey Number is probably a better place to submit. There seems to be some problem with the testcases on ICPC Live Archive (AC on Codechef gets WA there; Noone has solved it).
The suboptimal solution is very clever
There is another cool way of visualizing/memorizing SOS that I learnt from errichto's video:
How do you transform a 1D array to its prefix sum? You do:
a[i] += a[i - 1].How do you transform a 2D array to its prefix sum? Normally it is done by
p[i][j] = p[i-1][j] + p[i][j-1] - p[i-1][j-1] + a[i][j]. But notice that you can also apply the 1D prefix sum in rows and columns separately:Now, the sub over submasks problem can be imagined as doing a prefix sum on $$$2\times 2\times\ldots \times2$$$ hypercube! For example, lets say the mask has three bits, and you want sum over submasks for $$$101$$$. That is equivalent to taking the sum from cell $$$(0, 0, 0)$$$ to $$$(1, 0, 1)$$$ on a 3D cube.
So, you can just apply 1D prefix sum on each dimension separately. That is exactly what the final version of the code snippet is doing. It first iterates on the dimension, then does
a[..][1][..] += a[..][0][..]for that dimension; in other words, takes prefix sum on that dimension. And after that, the initial array turns into the SOS!Very interesting visualization. Thanks!
Can you please post the link to that video of Errichto's?
Watch analysis of the first problem here: Innopolis Open 2018-19 analysis
Analysis of the 2nd problem (B: Cake Tasting) it is, actually.
Link at the exact time if someone needs it.
Thanks. Made my understanding of the situation clear.
Kindly note that these relations form a directed acyclic graph and not necessarily a rooted tree (think about different values of mask and same value of i)
can someone explain not a rooted tree more
Can anyone please help me out in the question — VIM WAR ? Couldn't understand the summation formula in the editorial. Thankyou.
Did you get it? I am also facing problem understanding it.
Can we use
F[mask] = (1 << (__builtin_popcount(mask) - 1)) * a[badbit] + F[nmask] * 2;to update F[mask] in $$$O(1)$$$ wherebadbit = 31 - __builtin_clz(mask)andnmask = mask - (1 << badbit)?for(int i = 0; i<(1<<N); ++i)
for(int i = 0;i < N; ++i) for(int mask = 0; mask < (1<<N); ++mask){
}
let there be two numbers i and j such that i and j bit are set in mask then will f[mask^(1<<j)^(1<<i)] not added twice in f[mask] from above approach
wq
F[i] = A[i]????? why?, did u check your code with some examples?
its the memory optimized code in the blog i just copied it here.
f[i]=a[i] is initialization for all masks beacause every set is subset of itself ofc!
you are right, sorry for my wrong reply
Can I use FWT to solve this problem with the same complexity? F = FWT_AND(A,B),where B=[1,1,1,1...]
Easy ques, just above code: link
soln : link SAME AS ABOVE
thanks
can I get link of the same problem which discussed above Actually I want to check a little different approach
issue solved
This problem from csacademy uses SOS dp as a subroutine. Maybe checking it out.
If I need to iterate over the subsets of the mask's complement , How can I apply SoS DP approach? I'm able to apply the 3^N approach easily, However N is upto 20 which would lead to A TLE verdict.
usaxena95 any thoughts?
here is the problem if anyone is interested :101666G - Going Dutch
It seems isomorphic to this problem I ran into a few weeks ago. You'll have to change your DP from "How big is the largest valid partition of (the complement of) this mask?" to "How big is the largest valid partition of any subset of (the complement of) this mask?"
Edit : I get it now , here is the code in case someone needs it
Very well explained tutorial! it was very helpful. Thank you UwU
I have $$$Q \le 200000$$$ queries and set of $$$N \le 200000$$$ bitmasks. For each bitmask in query I have to calculate number of bitmasks in set that have a
bitwise ANDequal to $$$0$$$ with bitmask from query. How can I solve it, if bitmasks contains $$$50$$$ bits? I already can solve it for $$$20$$$ bits, but can't figure out sparse solution. I thought about something like:but it is directed acyclic graph...
Almost same article with lot more explanations — Link
The article linked has exactly same content. That one is blatantly copied, without even citing this blog as reference.
Cant get link for Special Pairs.
Quite an old problem I guess. They removed it.
Hey, I really liked your tutorial. Thanks for this blog. If you want, you can add this problem to your list ANDPREF
https://discuss.codechef.com/t/count-all-ordered-pairs-with-bitwise-and-equals-to-zero/36081
you can use this to get the problem statement if this helps.
UPD: https://www.hackerearth.com/problem/algorithm/find-the-number-of-ordered-pairs-1/
found the problem
Here's problem from CSES Problemset using this technique: https://cses.fi/problemset/task/1654.
A small reminder, we can change
if(mask & (1<<i))toif (!(mask & (1<<i))), then we can calculate the sum of super set (not subset).The correctness is simple, we can just change the dp formular above a bit.
And it can easily solve problem D in yesterday contest.
Thank you! I finally passed that problem!
or you can keep the if condition same and do F[mask&(1<<i)] += F[mask]; Just adding supersets to the set instead of adding subsets to the set.
How to prove complexity in the suboptimal solution? I haven't got how to come to 3^n through the sum.
https://cp-algorithms.com/algebra/all-submasks.html
omg, hadn't thought about binomial theorem here, thanks
Sorry for necroposting, but is there a way to fix the latex/markup sections? I keep on seeing
Unable to parse markup [type=CF_TEX]. usaxena95View the cached one here : https://webcache.googleusercontent.com/search?q=cache:NZrcJXh-IVkJ:https://mirror.codeforces.com/blog/entry/45223+&cd=1&hl=en&ct=clnk&gl=in
Thanks. I'm investigating the reason. Will be fixed soon.
I was reading this and started to solve the problems and suddenly whole blog just started showing this. Now I can't see the blog.
Unable to parse markup [type=CF_MARKDOWN]
Thanks, fixed now.
I seem to have seen this trick a long time ago, But I forgot it in today's contest ;)
Thanks!
Can anyone explain the approach involved in Covering Sets (problem 4) I get the sos dp part but how are we calculating the total sum for all triplets
Great tutorial, without it I would not be able to understand and solve https://mirror.codeforces.com/contest/1903/problem/D2.