Codeforces Round #359 Editorial

#	User	Rating
1	tourist	3985
2	jiangly	3814
3	jqdai0815	3682
4	Benq	3529
5	orzdevinwang	3526
6	ksun48	3517
7	Radewoosh	3410
8	hos.lyric	3399
9	ecnerwala	3392
9	Um_nik	3392

#	User	Contrib.
1	cry	169
2	maomao90	162
2	Um_nik	162
2	atcoder_official	162
5	djm03178	158
6	-is-this-fft-	157
7	adamant	155
8	awoo	154
8	Dominater069	154
10	nor	150

If you notice typos or errors, please send a private message.

Author: cdkrot
Developer: ch_egor

You just needed to implement the actions described in statement.

If you solution failed, then you probably forgot to use 64-bit integers or made some small mistake.

Correct solution:

C++ code

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <string>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <deque>
#include <set>
#include <map>
#include <cassert>
#include <algorithm>
#include <iomanip>
#include <ctime>
#include <cmath>
#include <bitset>

#pragma comment(linker, "/STACK:256000000")

using namespace std;

typedef long long int int64;
typedef long double double80;

const int INF = (1 << 29) + 5;
const int64 LLINF = (1ll << 59) + 5;
const int MOD = 1000 * 1000 * 1000 + 7;

const int MAX_N = 1005;

int n, x, sad;
int64 answer;

int main()
{
	//freopen("input.txt", "r", stdin);
	//freopen("output.txt", "w", stdout);

	scanf("%d %d\n", &n, &x);

	answer = x;
	sad = 0;

	int cur;
	char type;
	for (int i = 0; i < n; ++i)
	{
		scanf("%c %d\n", &type, &cur);
		if (type == '+')
		{
			answer += cur;
		}
		else if (answer >= cur)
		{
			answer -= cur;
		}
		else
		{
		    ++sad;
		}
	}

	cout << answer << " " << sad << "\n";

	fclose(stdin);
	fclose(stdout);

	return 0;
}

Python code

import sys

def main():
    n, answer = map(int, sys.stdin.readline().split())
    sad = 0

    for i in range(n):
        type_of, cur = sys.stdin.readline().split()
        cur = int(cur)
        if type_of == "+":
            answer += cur
        elif answer >= cur:
            answer -= cur
        else:
            sad += 1

    sys.stdout.write(str(answer) + " " + str(sad))

main()

Div2B Little Robber Girl's Zoo

Author: ch_egor
Developer: ch_egor

We need to sort an array with strange operations — namely, to swap elements with even and odd indices in subarray of even length. Note that we can change the 2 neighboring elements, simply doing our exchange action for subarray of length 2 containing these elements. Also, note that n ≤ 100, and it is permission to do 20 000 actions, therefore, we can write any quadratic sort, which changes the neighboring elements in each iteration (bubble sort for example).
Complexity O(n²)

C++ code

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <string>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <deque>
#include <set>
#include <map>
#include <cassert>
#include <algorithm>
#include <iomanip>
#include <ctime>
#include <cmath>
#include <bitset>

#pragma comment(linker, "/STACK:256000000")

using namespace std;

typedef long long int int64;
typedef long double double80;

const int INF = (1 << 29) + 5;
const int64 LLINF = (1ll << 59) + 5;
const int MOD = 1000 * 1000 * 1000 + 7;

const int MAX_N = 105;

int n;
int arr[MAX_N];

int main()
{
	//freopen("input.txt", "r", stdin);
	//freopen("output.txt", "w", stdout);

	scanf("%d", &n);

	for (int i = 0; i < n; ++i)
	{
		scanf("%d", &arr[i]);
	}

	for (int i = n - 1; i > 0; --i)
	{
		for (int j = 0; j < i; ++j)
		{
			if (arr[j] > arr[j + 1])
			{
				swap(arr[j], arr[j + 1]);
				printf("%d %d\n", j + 1, j + 2);
			}
		}
	}

	fclose(stdin);
	fclose(stdout);

	return 0;
}

Python code

n = int(input())
arr = list(map(int, input().split()))

for i in range(n - 1, 0, -1):
    for j in range(i):
        if arr[j] > arr[j + 1]:
            arr[j], arr[j + 1] = arr[j + 1], arr[j]
            print(j + 1, j + 2)

Bonus: Is anyone able to search the shortest solution of this problem? If yes, what complexity?

Div2C Robbers' watch/Div1A Robbers' watch

Author: cdkrot
Developer: themikemikovi4

In this problem we use the septimal number system. It is a very important limitation. Let's count how many digits are showed on the watch display and call it cnt. If cnt more than 7, the answer is clearly 0 (because of pigeonhole principle). If cnt is not greater than 7, then you can just bruteforces all cases.
Depending on the implementation it will be O(BASE BASE^BASE), O(BASE^BASE) or O(BASE BASE!), where BASE = 7. Actually the most simple implementation is just to cycle between all posible hour:minute combinations and check them.
In the worst case, it will work in O(BASE BASE^BASE).

C++ code

// Copyright (C) 2016 Sayutin Dmitry.
//
// This program is free software; you can redistribute it and/or
// modify it under the terms of the GNU General Public License as
// published by the Free Software Foundation; version 3

// This program is distributed in the hope that it will be useful,
// but WITHOUT ANY WARRANTY; without even the implied warranty of
// MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
// GNU General Public License for more details.

// You should have received a copy of the GNU General Public License
// along with this program; If not, see <http://www.gnu.org/licenses/>.


#include <iostream>
#include <vector>
#include <stdint.h>
#include <algorithm>
#include <set>
#include <map>
#include <array>
#include <queue>
#include <stack>
#include <functional>
#include <utility>
#include <string>
#include <assert.h>
#include <iterator>

using std::cin;
using std::cout;
using std::cerr;

using std::vector;
using std::map;
using std::array;
using std::set;
using std::string;

using std::pair;
using std::make_pair;

using std::min;
using std::abs;
using std::max;

using std::sort;
using std::generate;
using std::min_element;
using std::max_element;

template <typename T>
T input() {
    T res;
    cin >> res;
    return res;
}

int main() {
    std::iostream::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    size_t n, m;
    cin >> n >> m;

    size_t len1 = 1, len2 = 1;
    for (size_t a = 7; a < n; a *= 7)
        len1 += 1;
    for (size_t b = 7; b < m; b *= 7)
        len2 += 1;

    size_t ans = 0;
    if (len1 + len2 <= 7)
        for (size_t i = 0; i != n; ++i)
            for (size_t j = 0; j != m; ++j) {
                vector<size_t> used(7, 0);
                
                for (size_t a = i, k = 0; k != len1; a /= 7, ++k)
                    used[a % 7] += 1;
                for (size_t b = j, k = 0; k != len2; b /= 7, ++k)
                    used[b % 7] += 1;
                
                if (*std::max_element(used.begin(), used.end()) <= 1)
                    ++ans;
            }
    
    cout << ans << "\n";
    
    return 0;
}

Python code

BASE = 7

def itov(x):
    digits = []
    if x == 0:
        digits.append(0)
    while x > 0:
        digits.append(x % BASE)
        x //= BASE
    digits.reverse()
    return digits

def gen(pos = 0, minute = False, smaller = False):
    max_val = max_minute if minute else max_hour
    if pos >= len(max_val):
        if minute:
            return 1
        else:
            return gen(0, True)
    else:
        ans = 0
        for digit in range(BASE):
            if not used[digit] and (smaller or digit <= max_val[pos]):
                used[digit] = True
                ans += gen(pos + 1, minute, smaller or digit < max_val[pos])
                used[digit] = False
        return ans

n, m = map(int, input().split())
n -= 1
m -= 1
used = [False] * BASE
max_hour = itov(n)
max_minute = itov(m)
print(gen())

Bonus: Suppose the base is not fixed. Solve a problem with n ≤ 10⁹, m ≤ 10⁹, BASE ≤ 10⁹. Can you do it in 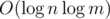$\text{[math]}$ ?

Div2D Kay and Snowflake/Div1B Kay and Snowflake

Author: cdkrot
Developers: ch_egor, cdkrot

There are many possible approaches.

Solution by cdkrot:

Look at the all candidates for the centroid of the vertices v subtree. The size of centroid subtree must be at least $\text{[math]}$ of the vertex v subtree size. (If it isn't, then after cutting the upper part will have too big size)

Choose the vertex with the smallest subtree size satisfying the constraint above. Let's prove, that this vertex is centroid indeed. If it isn't, then after cutting some part will have subtree size greater than $\text{[math]}$ of subtree size of query vertex. It isn't upper part (because of constraint above), it is one of our sons. Ouch, it's subtree less than of selected vertex, and it's still greater than $\text{[math]}$ of subtree size of query vertex. Contradiction.

So we find a centroid.
We write the euler tour of tree and we will use a 2D segment tree in order to search for a vertex quickly.
Complexity 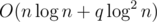$\text{[math]}$

C++ code

// Copyright (C) 2016 Sayutin Dmitry.
//
// This program is free software; you can redistribute it and/or
// modify it under the terms of the GNU General Public License as
// published by the Free Software Foundation; version 3

// This program is distributed in the hope that it will be useful,
// but WITHOUT ANY WARRANTY; without even the implied warranty of
// MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
// GNU General Public License for more details.

// You should have received a copy of the GNU General Public License
// along with this program; If not, see <http://www.gnu.org/licenses/>.


#include <iostream>
#include <vector>
#include <stdint.h>
#include <algorithm>
#include <set>
#include <map>
#include <array>
#include <queue>
#include <stack>
#include <functional>
#include <utility>
#include <string>
#include <assert.h>
#include <iterator>

using std::cin;
using std::cout;
using std::cerr;

using std::vector;
using std::map;
using std::array;
using std::set;
using std::string;

using std::pair;
using std::make_pair;

using std::min;
using std::abs;
using std::max;

using std::sort;
using std::generate;
using std::min_element;
using std::max_element;

template <typename T>
T input() {
    T res;
    cin >> res;
    return res;
}

const size_t MAXN = (1 << 19);
vector<size_t> graph[MAXN];

vector<pair<size_t, size_t>> segm[2 * MAXN - 1];

#define time TIME_FUCKLIBC

pair<size_t, size_t> times[MAXN];
size_t time = 0;

size_t sizes[MAXN];

void dfs(size_t v) {
    size_t sz = 1;
    
    times[v].first = time++;

    for (size_t u: graph[v]) {
        dfs(u);
        sz += sizes[u];
    }
    
    times[v].second = time;
    segm[MAXN - 1 + times[v].first].emplace_back(sz, v);
    
    sizes[v] = sz;
}

void buildseg(size_t node, size_t L, size_t R) {
    if (L != R - 1) {
        size_t mid = L + (R - L) / 2;
        buildseg(2 * node + 1, L, mid);
        buildseg(2 * node + 2, mid, R);
        
        segm[node].resize(segm[2 * node + 1].size() + segm[2 * node + 2].size());
        std::merge(segm[2 * node + 1].begin(), segm[2 * node + 1].end(), segm[2 * node + 2].begin(), segm[2 * node + 2].end(), segm[node].begin());
    }
}

pair<size_t, size_t> lowerb(size_t node, size_t L, size_t R, size_t rl, size_t rr, pair<size_t, size_t> minval) {
    if (rl <= L and R <= rr) {
        auto it = std::lower_bound(segm[node].begin(), segm[node].end(), minval);
        if (it == segm[node].end())
            return make_pair(SIZE_MAX, SIZE_MAX);
        else
            return *it;
    }
    if (R <= rl or rr <= L)
        return make_pair(SIZE_MAX, SIZE_MAX);

    size_t mid = L + (R - L) / 2;
    return min(lowerb(2 * node + 1, L, mid, rl, rr, minval)
              ,lowerb(2 * node + 2, mid, R, rl, rr, minval));
}

int main() {
    std::iostream::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    size_t n, q;
    cin >> n >> q;
    
    for (size_t i = 1; i != n; ++i)
        graph[input<size_t>() - 1].push_back(i);

    dfs(0);
    buildseg(0, 0, MAXN);
    
    for (size_t i = 0; i != q; ++i) {
        size_t v = input<size_t>() - 1;
        cout << lowerb(0, 0, MAXN, times[v].first, times[v].second, make_pair((sizes[v] + 1) / 2, 0)).second + 1 << "\n";
    }
    
    return 0;
}

You can consider all answers by one in dfs using this idea. Use std::set for pair (subtree size, vertex number) and at each vertex merge sets obtained from children. (Also known as "merging sets" idea)
Thus we get the answers for all vertex and we need only output answers for queries.
Complexity 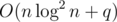$\text{[math]}$

C++ code

// Copyright (C) 2016 Sayutin Dmitry.
//
// This program is free software; you can redistribute it and/or
// modify it under the terms of the GNU General Public License as
// published by the Free Software Foundation; version 3

// This program is distributed in the hope that it will be useful,
// but WITHOUT ANY WARRANTY; without even the implied warranty of
// MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
// GNU General Public License for more details.

// You should have received a copy of the GNU General Public License
// along with this program; If not, see <http://www.gnu.org/licenses/>.


#include <iostream>
#include <vector>
#include <stdint.h>
#include <algorithm>
#include <set>
#include <map>
#include <array>
#include <queue>
#include <stack>
#include <functional>
#include <utility>
#include <string>
#include <assert.h>
#include <iterator>

using std::cin;
using std::cout;
using std::cerr;

using std::vector;
using std::map;
using std::array;
using std::set;
using std::string;

using std::pair;
using std::make_pair;

using std::min;
using std::abs;
using std::max;

using std::sort;
using std::generate;
using std::min_element;
using std::max_element;

template <typename T>
T input() {
    T res;
    cin >> res;
    return res;
}

set<pair<size_t, size_t>> solve(const vector<vector<size_t>>& graph, vector<size_t>& ans, size_t v) {
    set<pair<size_t, size_t>> cur;

    for (size_t u: graph[v]) {
        auto ch = solve(graph, ans, u);
        if (not (ch.size() < cur.size()))
            std::swap(ch, cur);
        
        for (auto elem: ch)
            cur.insert(elem);
    }

    size_t sz = cur.size() + 1;
    cur.emplace(sz, v);

    ans[v] = cur.lower_bound(make_pair((sz + 1) / 2, 0))->second;
    
    return std::move(cur);
}

int main() {
    std::iostream::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    size_t n, q;
    cin >> n >> q;
    
    vector<vector<size_t>> graph(n);
    for (size_t i = 1; i != n; ++i)
        graph[input<size_t>() - 1].push_back(i);

    vector<size_t> ans(n, SIZE_MAX);

    solve(graph, ans, 0);
    
    for (size_t i = 0; i != q; ++i)
        cout << ans[input<size_t>() - 1] + 1 << "\n";
    
    return 0;
}

Solution by ch_egor:
Solve it for all subtrees. We can solve the problem for some subtree, after solving the problem for all of it's children. Let's choose the heaviest child. Note that the centroid of the child after a certain lifting goes into our centroid. Let's model the lifting.
Thus we get the answers for all vertex and we need only output answers for queries.
Complexity O(n + q)

C++ code

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <string>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <deque>
#include <set>
#include <map>
#include <cassert>
#include <algorithm>
#include <iomanip>
#include <ctime>
#include <cmath>
#include <bitset>

#pragma comment(linker, "/STACK:256000000")

using namespace std;

typedef long long int int64;
typedef long double double80;

const int INF = (1 << 29) + 5;
const int64 LLINF = (1ll << 59) + 5;
const int MOD = 1000 * 1000 * 1000 + 7;

const int MAX_N = 300 * 1000 + 5;
const int MAX_Q = 300 * 1000 + 5;

int n, q;
vector<int> graph[MAX_N];
int size_of[MAX_N];
int prev_of[MAX_N];
int big_subtree[MAX_N];
int centroid[MAX_N];

bool is_centroid_of_subtree(int v, int c)
{
	return ((size_of[v] - size_of[c]) * 2 <= size_of[v] && big_subtree[c] * 2 <= size_of[v]);
}

void dfs_calc(int v, int p)
{
	big_subtree[v] = 0;
	size_of[v] = 1;
	prev_of[v] = p;

	for (int i = 0; i < graph[v].size(); ++i)
	{
		dfs_calc(graph[v][i], v);
		size_of[v] += size_of[graph[v][i]];
		big_subtree[v] = max(big_subtree[v], size_of[graph[v][i]]);
	}
}

void dfs_centroid(int v)
{
	if (size_of[v] == 1)
	{
		centroid[v] = v;
	}
	else
	{
		int ptr = 0;
		for (int i = 0; i < graph[v].size(); ++i)
		{
			dfs_centroid(graph[v][i]);
			if (size_of[graph[v][ptr]] < size_of[graph[v][i]])
			{
				ptr = i;
			}
		}

		int c = centroid[graph[v][ptr]];

		while (!is_centroid_of_subtree(v, c))
		{
			c = prev_of[c];
		}

		centroid[v] = c;
	}
}

int main()
{
	//freopen("input.txt", "r", stdin);
	//freopen("output.txt", "w", stdout);

	scanf("%d %d", &n, &q);

	int v;
	for (int i = 0; i < n - 1; ++i)
	{
		scanf("%d", &v);
		graph[v - 1].push_back(i + 1);
	}

	dfs_calc(0, 0);
	dfs_centroid(0);

	for (int i = 0; i < q; ++i)
	{
		scanf("%d", &v);
		printf("%d\n", centroid[v - 1] + 1);
	}

	fclose(stdin);
	fclose(stdout);

	return 0;
}

Div2E Optimal Point/Div1C Optimal Point

Author: cdkrot
Developer: cdkrot

Let's say few words about ternary search. It works correctly, but too slow.
It's complexity is 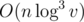$\text{[math]}$ , where n = 10⁵, and v = 10¹⁸.
Don't use it.

Solution.
1) Let's make binary search on answer
2) Consider areas of "good" points (with dist ≤ mid) for each source point.
3) Intersect those areas and check for solution.

This area can be decsribed by following inequalities:
(You can achieve them if you expand modules in inequality "manhattan distance <= const")

.. ≤ x + y + z ≤ ..

.. ≤ - x + y + z ≤ ..

.. ≤ x - y + z ≤ ..

.. ≤ x + y - z ≤ ..

.. denote some constants.

If you intersect set of such system, you will get system of the same form, so let's learn how to solve such system.

Let's replace some variables:

a = - x + y + z

b = x - y + z

c = x + y - z

Then:

x + y + z = a + b + c

x = (b + c) / 2

y = (a + c) / 2

z = (a + b) / 2

Now the system transforms into:

.. ≤ a ≤ ..

.. ≤ b ≤ ..

.. ≤ c ≤ ..

.. ≤ a + b + c ≤ ..

We need to check if the system has solution in integers, also the numbers a, b, c must be of the same parity (have equal remainder after division by 2). (This is required for x, y, z to be integers too)

Let's get rid of parity constraint. Bruteforce the parity of a, b, c (two cases)

Make following replacement: a = 2a' + r, b = 2b' + r, c = 2c' + r, where r = 0 or r = 1. Substitute in equations above, simplify, and gain the same system for a', b', c' without parity constraint.

And now the system can be solved greedy (At first set a, b, c with minimum, and then raise slowly if necessary).

Total complexity is 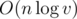$\text{[math]}$ .

C++ code

// Copyright (C) 2016 Sayutin Dmitry.
//
// This program is free software; you can redistribute it and/or
// modify it under the terms of the GNU General Public License as
// published by the Free Software Foundation; version 3

// This program is distributed in the hope that it will be useful,
// but WITHOUT ANY WARRANTY; without even the implied warranty of
// MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
// GNU General Public License for more details.

// You should have received a copy of the GNU General Public License
// along with this program; If not, see <http://www.gnu.org/licenses/>.


#include <iostream>
#include <vector>
#include <stdint.h>
#include <algorithm>
#include <set>
#include <map>
#include <array>
#include <queue>
#include <stack>
#include <functional>
#include <utility>
#include <string>
#include <assert.h>
#include <iterator>

using std::cin;
using std::cout;
using std::cerr;

using std::vector;
using std::map;
using std::array;
using std::set;
using std::string;

using std::pair;
using std::make_pair;

using std::min;
using std::abs;
using std::max;

using std::sort;
using std::generate;
using std::min_element;
using std::max_element;

template <typename T>
T input() {
    T res;
    cin >> res;
    return res;
}

struct coord {
    int64_t x;
    int64_t y;
    int64_t z;
};

struct equation {
    pair<int64_t, int64_t> S;
    pair<int64_t, int64_t> a;
    pair<int64_t, int64_t> b;
    pair<int64_t, int64_t> c;
};

vector<coord> list;

equation operator+(const equation& e1, const equation& e2) {
    equation res;
    res.S = {max(e1.S.first, e2.S.first), min(e1.S.second, e2.S.second)};
    res.a = {max(e1.a.first, e2.a.first), min(e1.a.second, e2.a.second)};
    res.b = {max(e1.b.first, e2.b.first), min(e1.b.second, e2.b.second)};
    res.c = {max(e1.c.first, e2.c.first), min(e1.c.second, e2.c.second)};
    return res;
}

coord get_solution(const equation& eq) {
    if ((eq.S.first > eq.S.second)
     or (eq.a.first > eq.a.second)
     or (eq.b.first > eq.b.second)
     or (eq.c.first > eq.c.second))
        return coord {INT64_MAX, INT64_MAX, INT64_MAX};
        
     if ((eq.a.first + eq.b.first + eq.c.first > eq.S.second)
     or (eq.a.second + eq.b.second + eq.c.second < eq.S.first))
        return coord {INT64_MAX, INT64_MAX, INT64_MAX};

     coord res;
     res.x = eq.a.first;
     res.y = eq.b.first;
     res.z = eq.c.first;
     int64_t delta = max(int64_t(0), eq.S.first - res.x - res.y - res.z);

     res.x += min(delta, eq.a.second - eq.a.first);
     delta -= min(delta, eq.a.second - eq.a.first);
     res.y += min(delta, eq.b.second - eq.b.first);
     delta -= min(delta, eq.b.second - eq.b.first);
     res.z += min(delta, eq.c.second - eq.c.first);
     delta -= min(delta, eq.c.second - eq.c.first);

     assert(delta == 0);
     
     return res;
}

int64_t DIV2(int64_t arg) {
    return (arg - (arg & 1)) / 2;
}

coord can(int64_t MAXANS) {
    equation eq;
    eq.S = eq.a = eq.b = eq.c = {INT64_MIN, INT64_MAX};
    
    for (const coord& crd: list) {
        equation nw;
        nw.S = { crd.x + crd.y + crd.z - MAXANS,  crd.x + crd.y + crd.z + MAXANS};
        nw.a = {-crd.x + crd.y + crd.z - MAXANS, -crd.x + crd.y + crd.z + MAXANS};
        nw.b = { crd.x - crd.y + crd.z - MAXANS,  crd.x - crd.y + crd.z + MAXANS};
        nw.c = { crd.x + crd.y - crd.z - MAXANS,  crd.x + crd.y - crd.z + MAXANS};
        
        eq = eq + nw;
    }

    for (int64_t r = 0; r <= 1; ++r) {
        equation tr = eq;

        tr.S.first  = DIV2(tr.S.first - 3 * r + 1);
        tr.a.first  = DIV2(tr.a.first - r + 1);
        tr.b.first  = DIV2(tr.b.first - r + 1);
        tr.c.first  = DIV2(tr.c.first - r + 1);

        tr.S.second = DIV2(tr.S.second - 3 * r);
        tr.a.second = DIV2(tr.a.second - r);
        tr.b.second = DIV2(tr.b.second - r);
        tr.c.second = DIV2(tr.c.second - r);

        coord sol = get_solution(tr);
        if (sol.x != INT64_MAX) {
            coord ans;
            ans.x = r + sol.y + sol.z;
            ans.y = r + sol.x + sol.z;
            ans.z = r + sol.x + sol.y;

            return ans;
        }
    }
    return coord {INT64_MAX, INT64_MAX, INT64_MAX};
}

int main() {
    std::iostream::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    list.reserve(100000);
    
    for (size_t T = input<size_t>(); T != 0; --T) {
        list.resize(input<size_t>());
        
        for (coord& crd: list)
            cin >> crd.x >> crd.y >> crd.z;

        int64_t L = -1; // definitely imposible
        int64_t R = 3 * int64_t(1000 * 1000 * 1000) * int64_t(1000 * 1000 * 1000) + 10; // definitely possible

        while (R - L > 1) {
            int64_t M = L + (R - L) / 2;
            if (can(M).x != INT64_MAX)
                R = M;
            else
                L = M;
        }
        coord ans = can(R);
        cout << ans.x << " " << ans.y << " " << ans.z << "\n";
    }
    
    return 0;
}

Bonus. This task can be solved in a lot of modifications, for example euclidian distance instead of manhattan, 2d instead of 3d, floats instead of integers. How to solve this varations?

Div1D Kay and Eternity

Authors: platypus179, Endagorion
Developer: platypus179

Let's solve this problem with scanline. Go through all rows from left to right and maintain the array in which in j index we will store the number of points in a square with bottom left coordinate (i, j), where i is current row of scanline.

This takes O(MAXCORD²) time. Note that the set of squares that contain some of the shaded points is not very large, namely — if the point has coordinates (x, y), then the set of left bottom corners of square is defined as {(a, b)|x - k + 1 < = a < = x, y - k + 1 < = b < = y}. Let's consider each point (x, y) as the 2 events:
Add one to the all elements with indexes from y - k + 1 to y on the row x - k + 1 and take one at the same interval on the row x + 1. How to calculate answer? Suppose we update the value of a cell on the row a, and before it was updated the value x on the row b. Let add to the answer for the number of squares containing x points value a - b. We can implement the addition of the segment directly and have O(nk) for processing all the events that fit in time limit. To get rid of O(MAXCORD) memory, we need to write all interested in the coordinates before processing events (them no more than nk) and reduce the coordinates in the events. It takes 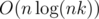$\text{[math]}$ time and O(nk) memory. Now we can execute the previous point in O(nk) memory.
Complexity is 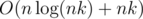$\text{[math]}$ time and O(nk) memory.

C++ code

#include <iostream>
#include <cstdio>
#include <vector>
#include <string>
#include <algorithm>

using namespace std;
typedef long long ll;

#define NotANumber -1791791791

struct query {
    int row, l, r; bool a;
    int lbl, ubr;
    query(int _row, int _l, int _r, bool _a) {row = _row; l = _l; r = _r; a = _a;}
    bool operator<(const query& other) const {
        return row < other.row;
    }
};

int main() {
    int n, k;
    scanf("%d %d", &n, &k);
    vector<pair<int, int> > points(n);
    for (int i = 0; i < n; i++)
        scanf("%d %d", &points[i].first, &points[i].second);

    sort(points.begin(), points.end());
    vector<int> xcoords;
    for (int i = 0; i < n; i++) {
        int st;
        if (xcoords.empty())
            st = points[i].first - k + 1;
        else
            st = max(xcoords.back() + 1, points[i].first - k + 1);
        for (int j = st; j <= points[i].first; j++)
            xcoords.push_back(j);
    }

    vector<query> qs;
    for (int i = 0; i < n; i++) {
        qs.push_back(query(points[i].second - k + 1, points[i].first - k + 1, points[i].first, 1));
        qs.push_back(query(points[i].second + 1, points[i].first - k + 1, points[i].first, 0));
    }

    for (query & q : qs) {
        q.lbl = lower_bound(xcoords.begin(), xcoords.end(), q.l) - xcoords.begin();
        q.ubr = upper_bound(xcoords.begin(), xcoords.end(), q.r) - xcoords.begin();
    }
    
    int xcdssz = xcoords.size();
    xcoords.clear();
    xcoords.shrink_to_fit();

    sort(qs.begin(), qs.end());

    vector<int> vec(xcdssz, 0);
    vector<int> lastchanged(xcdssz, NotANumber);
    vector<ll> ans(n);

    for (query q : qs) {
        int lbl = q.lbl;
        int ubr = q.ubr;
        for (int i = lbl; i < ubr; i++) {
            if (lastchanged[i] != NotANumber && vec[i] != 0) {
                ans[vec[i] - 1] += q.row - lastchanged[i];
            }
            if (q.a)
                vec[i]++;
            else
                vec[i]--;
            lastchanged[i] = q.row;
        }
    }

    for (int i = 0; i < n; i++)
        printf("%lld ", ans[i]);
    printf("\n");
    return 0;
}

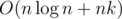Bonus: $\text{[math]}$ time and O(n) memory.

C++ code

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <string>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <deque>
#include <set>
#include <map>
#include <cassert>
#include <algorithm>
#include <iomanip>
#include <ctime>
#include <cmath>
#include <bitset>

#pragma comment(linker, "/STACK:256000000")

using namespace std;

typedef long long int int64;
typedef long double double80;

const int INF = (1 << 29) + 5;
const int64 LLINF = (1ll << 59) + 5;
const int MOD = 1000 * 1000 * 1000 + 7;

const int MAX_N = 1000 * 100 + 5;
const int MAX_K = 305;

/** Interface */

inline int readChar();
template <class T = int> inline T readInt();
template <class T> inline void writeInt(T x);
inline void writeChar(int x);
inline void writeWord(const char *s);
inline void flush();

/** Read */

static const int buf_size = 20 * 1000 * 1000;

inline int getChar()
{
	static char buf[buf_size];
	static int len = 0, pos = 0;
	if (pos == len)
		pos = 0, len = fread(buf, 1, buf_size, stdin);
	if (pos == len)
		return -1;
	return buf[pos++];
}

inline int readChar()
{
	int c = getChar();
	while (c <= 32)
		c = getChar();
	return c;
}

template <class T>
inline T readInt()
{
	int s = 1, c = readChar();
	T x = 0;
	if (c == '-')
		s = -1, c = getChar();
	while ('0' <= c && c <= '9')
		x = x * 10 + c - '0', c = getChar();
	return s == 1 ? x : -x;
}

inline int64 readInt64()
{
	int s = 1, c = readChar();
	int64 x = 0;
	if (c == '-')
		s = -1, c = getChar();
	while ('0' <= c && c <= '9')
		x = x * 10 + c - '0', c = getChar();
	return s == 1 ? x : -x;
}

/** Write */

static int write_pos = 0;
static char write_buf[buf_size];

inline void writeChar(int x)
{
	if (write_pos == buf_size)
		fwrite(write_buf, 1, buf_size, stdout), write_pos = 0;
	write_buf[write_pos++] = x;
}

inline void flush()
{
	if (write_pos)
		fwrite(write_buf, 1, write_pos, stdout), write_pos = 0;
}

template <class T>
inline void writeInt(T x)
{
	if (x < 0)
		writeChar('-'), x = -x;

	char s[24];
	int n = 0;
	while (x || !n)
		s[n++] = '0' + x % 10, x /= 10;
	while (n--)
		writeChar(s[n]);
}

inline void writeInt64(int64 x)
{
	if (x < 0)
		writeChar('-'), x = -x;

	char s[24];
	int n = 0;
	while (x || !n)
		s[n++] = '0' + x % 10, x /= 10;
	while (n--)
		writeChar(s[n]);
}

inline void writeWord(const char *s)
{
	while (*s)
		writeChar(*s++);
}

struct point
{
	int x;
	int y;
};

struct ask
{
	int l;
	int r;
	int ptr;
	int type;
};

bool cmp(const ask &a, const ask &b)
{
	return a.ptr < b.ptr;
}

int n, k;
point arr[MAX_N];
int cord[MAX_N * 2];
ask asks[MAX_N * 2];
int cord_len = 0;
int asks_len = 0;
bool have_prev_cord[MAX_N * 2];
bool have_prev_line[MAX_N * 2];
int last_of_cord[MAX_N * 2];
int last_of_line[MAX_N * 2];
int at_cord[MAX_N * 2];
int at_line[MAX_N * 2];
int64 answer[MAX_N];

int main()
{
	//freopen("input.txt", "r", stdin);
	//freopen("output.txt", "w", stdout);

	n = readInt();
	k = readInt();

	for (int i = 0; i < n; ++i)
	{
		arr[i].x = readInt();
		arr[i].y = readInt();
		cord[cord_len++] = arr[i].x;
		cord[cord_len++] = arr[i].x - k + 1;
	}

	sort(cord, cord + 2 * n);
	cord_len = unique(cord, cord + 2 * n) - cord;
	
	for (int i = 0; i < n; ++i)
	{
		asks[asks_len].l = lower_bound(cord, cord + cord_len, arr[i].x - k + 1) - cord;
		asks[asks_len].r = lower_bound(cord, cord + cord_len, arr[i].x) - cord;
		asks[asks_len].ptr = arr[i].y - k + 1;
		asks[asks_len].type = 1;
		++asks_len;
		asks[asks_len].l = asks[asks_len - 1].l;
		asks[asks_len].r = asks[asks_len - 1].r;
		asks[asks_len].ptr = arr[i].y + 1;
		asks[asks_len].type = -1;
		++asks_len;
	}

	sort(asks, asks + asks_len, cmp);
	memset(answer, 0, sizeof(answer));
	memset(last_of_cord, 0, sizeof(last_of_cord));
	memset(last_of_line, 0, sizeof(last_of_line));
	memset(at_cord, 0, sizeof(at_cord));
	memset(at_line, 0, sizeof(at_line));
	memset(have_prev_cord, 0, sizeof(have_prev_cord));
	memset(have_prev_line, 0, sizeof(have_prev_cord));

	for (int i = 0; i < asks_len; ++i)
	{
		for (int j = asks[i].l; j <= asks[i].r; ++j)
		{
			if (!have_prev_cord[j])
			{
				have_prev_cord[j] = true;
				last_of_cord[j] = asks[i].ptr;
				at_cord[j] += asks[i].type;
			}
			else
			{
				answer[at_cord[j]] += asks[i].ptr - last_of_cord[j];

				last_of_cord[j] = asks[i].ptr;
				at_cord[j] += asks[i].type;
			}
		

			if (j != asks[i].r)
			{
				if (!have_prev_line[j])
				{
					have_prev_line[j] = true;
					last_of_line[j] = asks[i].ptr;
					at_line[j] += asks[i].type;
				}
				else
				{
					answer[at_line[j]] += 1ll * (cord[j + 1] - cord[j] - 1) * (asks[i].ptr - last_of_line[j]);

					last_of_line[j] = asks[i].ptr;
					at_line[j] += asks[i].type;
				}
			}
		}
	}

	for (int i = 1; i <= n; ++i)
	{
		writeInt64(answer[i]);
		writeChar(' ');
	}

	flush();

	fclose(stdin);
	fclose(stdout);

	return 0;
}

Div1E Travelling Through the Snow Queen's Kingdom

Authors: cdkrot, GlebsHP
Developers: ch_egor, cdkrot

Unfortunately, due to my, cdkrot, failure, it was possible to get Ac with O(nm) solution, I apologise for that.

We propose following solution:
Let's solve task with divide & conquer. At first let's lift l to the first index, where s was mentioned And lower the r to the last index, where t was mentioned. This will not affect answers, but will make implementation much more easy.

Let's look on all queries. For each query consider it's location relative to centre of edges array. If it's stricly on the left half or on the right half, then solve recursively (You need to implement function like solve(requests, l, r)).

How to answer on query, if it contains the centre? Let's precalculate two dp's:

dp_r[i] = bitset of vertices you can from to the v_i or u_i with l = m and r = i.

dp_l[i] = bitset of vertices you can go to starting from v_i or u_i with l = i and r = m - 1

v_i and u_i are vertices of i'th edge.

Using this dp the answer is yes if and ony if dp_l[l][u] = true and dp_r[r][u] = true for some u.

All above can be implemented using bitwise operations.
So the time is 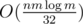$\text{[math]}$

C++ code

// Copyright (C) 2016 Sayutin Dmitry.
//
// This program is free software; you can redistribute it and/or
// modify it under the terms of the GNU General Public License as
// published by the Free Software Foundation; version 3

// This program is distributed in the hope that it will be useful,
// but WITHOUT ANY WARRANTY; without even the implied warranty of
// MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
// GNU General Public License for more details.

// You should have received a copy of the GNU General Public License
// along with this program; If not, see <http://www.gnu.org/licenses/>.


#include <iostream>
#include <vector>
#include <stdint.h>
#include <algorithm>
#include <set>
#include <map>
#include <array>
#include <queue>
#include <stack>
#include <functional>
#include <utility>
#include <string>
#include <assert.h>
#include <iterator>
#include <bitset>

using std::cin;
using std::cout;
using std::cerr;

using std::vector;
using std::map;
using std::array;
using std::set;
using std::string;

using std::pair;
using std::make_pair;

using std::min;
using std::abs;
using std::max;

using std::sort;
using std::generate;
using std::min_element;
using std::max_element;

#define size_t uint32_t

struct Req {
    size_t L;
    size_t R;
    size_t S;
    size_t T;
    size_t ID;
};

struct Edge {
    size_t v;
    size_t u;
    size_t prev1;
    size_t prev2;
    size_t next1;
    size_t next2;
};

const size_t MAXQ = 200000;
const size_t MAXN = 1000;
const size_t MAXM = 200000;

char answers[MAXQ];
Edge list[MAXM];
vector<size_t> last[MAXN];

std::bitset<MAXN> masks_r[MAXM / 2 + 10];
std::bitset<MAXN> masks_l[MAXM / 2 + 10];

void solve_layer(vector<Req>& requests, size_t l, size_t m, size_t r) {
    bool has = false;
    for (size_t i = 0; i != requests.size(); ++i)
        has or_eq (requests[i].L <= m - 1 and requests[i].R >= m);
    if (not has)
        return;
    
    for (size_t i = 0; i != r - m; ++i) {
        masks_r[i] = std::bitset<MAXN>();
        if (list[m + i].prev1 >= m and list[m + i].prev1 != std::numeric_limits<size_t>::max())
            masks_r[i] |= masks_r[list[m + i].prev1 - m];
        if (list[m + i].prev2 >= m and list[m + i].prev2 != std::numeric_limits<size_t>::max())
            masks_r[i] |= masks_r[list[m + i].prev2 - m];

        masks_r[i][list[m + i].v] = true;
        masks_r[i][list[m + i].u] = true;
    }
    
    for (size_t z = 0; z != m - l; ++z) {
        size_t i = (m - l) - 1 - z;
        masks_l[i] = std::bitset<MAXN>();
        
        if (list[l + i].next1 < m)
            masks_l[i] |= masks_l[list[l + i].next1 - l];
        if (list[l + i].next2 < m)
            masks_l[i] |= masks_l[list[l + i].next2 - l];
        masks_l[i][list[l + i].v] = true;
        masks_l[i][list[l + i].u] = true;
    }

    for (size_t i = 0; i != requests.size();)
        if (requests[i].L <= m - 1 and requests[i].R >= m) {
            answers[requests[i].ID] = (masks_r[requests[i].R - m] & masks_l[requests[i].L - l]).any();
            std::swap(requests[i], requests.back());
            requests.pop_back();
        } else {
            ++i;
        }
}

void solve(vector<Req>& requests, size_t l, size_t r) {
    if (l == r - 1) {
        for (auto& req: requests)
            answers[req.ID] = (req.S == list[l].v or req.S == list[l].u)
                          and (req.T == list[l].v or req.T == list[l].u);
        return;
    }
    size_t m = l + (r - l) / 2;
    // [l, m), [m, r).

    solve_layer(requests, l, m, r);

    vector<Req> right;
    for (size_t i = 0; i != requests.size();)
        if (requests[i].L >= m) {
            right.push_back(requests[i]);
            std::swap(requests[i], requests.back());
            requests.pop_back();
        } else {
            ++i;
        }

    requests.shrink_to_fit();
    solve(requests, l, m);
    solve(right, m, r);
}

int main() {
    size_t n, m, q;
    scanf("%d %d %d", &n, &m, &q);

    assert(n <= MAXN);
    assert(q <= MAXQ);
    assert(m <= MAXM);
    
    std::fill(answers, answers + q, 16);
    
    for (size_t i = 0; i != m; ++i) {
        scanf("%d %d", &list[i].v, &list[i].u);
        --list[i].v, --list[i].u;
        list[i].prev1 = list[i].prev2 = list[i].next1 = list[i].next2 = std::numeric_limits<size_t>::max();
        
        if (not last[list[i].v].empty()) {
            list[i].prev1 = last[list[i].v].back();
            
            if (list[last[list[i].v].back()].v == list[i].v)
                list[last[list[i].v].back()].next1 = i;
            else {
                list[last[list[i].v].back()].next2 = i;
            }
        }

        if (not last[list[i].u].empty()) {
            list[i].prev2 = last[list[i].u].back();
            
            if (list[last[list[i].u].back()].v == list[i].u)
                list[last[list[i].u].back()].next1 = i;
            else {
                list[last[list[i].u].back()].next2 = i;
            }
        }
        
        last[list[i].v].push_back(i);
        last[list[i].u].push_back(i);
    }

    vector<Req> requests;
    for (size_t i = 0; i != q; ++i) {
        Req req;
        scanf("%d %d %d %d", &req.L, &req.R, &req.S, &req.T);
        --req.L, --req.R, --req.S, --req.T;
        req.ID = i;
        
        auto it1 = std::lower_bound(last[req.S].begin(), last[req.S].end(), req.L);
        auto it2 = std::upper_bound(last[req.T].begin(), last[req.T].end(), req.R);

        if (it1 == last[req.S].end() or it2 == last[req.T].begin())
            answers[i] = false;
        else {
            req.L = *it1;
            req.R = *std::prev(it2);
            if (req.L > req.R)
                answers[i] = false;
            else
                requests.push_back(req);
        }
    }
    
    solve(requests, 0, m);

    for (size_t i = 0; i != q; ++i) {
        printf("%s", (answers[i] ? "Yes\n" : "No\n"));
    }
    
    return 0;
}

// Copyright (C) 2016 Sayutin Dmitry. // // This program is free software; you can redistribute it and/or // modify it under the terms of the GNU General Public License as // published by the Free Software Foundation; version 3 // This program is distributed in the hope that it will be useful, // but WITHOUT ANY WARRANTY; without even the implied warranty of // MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the // GNU General Public License for more details. // You should have received a copy of the GNU General Public License // along with this program; If not, see <http://www.gnu.org/licenses/>. #include <iostream> #include <vector> #include <stdint.h> #include <algorithm> #include <set> #include <map> #include <array> #include <queue> #include <stack> #include <functional> #include <utility> #include <string> #include <assert.h> #include <iterator> #include <bitset> using std::cin; using std::cout; using std::cerr; using std::vector; using std::map; using std::array; using std::set; using std::string; using std::pair; using std::make_pair; using std::min; using std::abs; using std::max; using std::sort; using std::generate; using std::min_element; using std::max_element; template <typename T> T input() { T res; cin >> res; return res; } const size_t MAX_N = ..; const size_t MAX_M = ..; template <typename T, size_t sz> struct supervec { public: T data[sz]; size_t used = 0; T& operator[](size_t id) { return data[id]; } void push_back(T val) { data[used++] = val; } T* begin() { return data; } T* end() { return data + used; } }; supervec<size_t, 2> graph[MAX_M]; vector<size_t> last[MAX_N]; std::bitset<MAX_M> dp[MAX_M]; int main() { std::iostream::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); size_t n, m, q; cin >> n >> m >> q; assert(n <= MAX_N and m <= MAX_M); for (size_t i = 0; i != m; ++i) { size_t v, u; cin >> v >> u; --v, --u; if (not last[v].empty()) graph[i].push_back(last[v].back()); if (not last[u].empty()) graph[i].push_back(last[u].back()); last[v].push_back(i); last[u].push_back(i); } for (size_t i = 0; i != m; ++i) { for (size_t u: graph[i]) dp[i] or_eq dp[u]; dp[i][i] = true; } for (size_t i = 0; i != q; ++i) { size_t L, R, S, T; cin >> L >> R >> S >> T; --L, --R, --S, --T; bool res = false; std::vector<size_t>::iterator it1, it2; it1 = std::lower_bound(last[S].begin(), last[S].end(), L); if (it1 == last[S].end()) goto end; L = *it1; it2 = std::upper_bound(last[T].begin(), last[T].end(), R); if (it2 == last[T].begin()) goto end; R = *std::prev(it2); res = dp[R][L]; end:; cout << (res ? "Yes\n" : "No\n"); } return 0; }

#include <iostream> #include <cstdio> #include <cstdlib> #include <string> #include <cstring> #include <vector> #include <stack> #include <queue> #include <deque> #include <set> #include <map> #include <cassert> #include <algorithm> #include <iomanip> #include <ctime> #include <cmath> #include <bitset> #pragma comment(linker, "/STACK:256000000") using namespace std; typedef long long int int64; typedef long double double80; const int INF = (1 << 29) + 5; const int64 LLINF = (1ll << 59) + 5; const int MOD = 1000 * 1000 * 1000 + 7; const int MAX_N = 1000 + 5; const int MAX_M = 200000 + 5; const int MAX_Q = 200000 + 5; /** Interface */ inline int readChar(); template <class T = int> inline T readInt(); template <class T> inline void writeInt(T x); inline void writeChar(int x); inline void writeWord(const char *s); inline void flush(); /** Read */ static const int buf_size = 20 * 1000 * 1000; inline int getChar() { static char buf[buf_size]; static int len = 0, pos = 0; if (pos == len) pos = 0, len = fread(buf, 1, buf_size, stdin); if (pos == len) return -1; return buf[pos++]; } inline int readChar() { int c = getChar(); while (c <= 32) c = getChar(); return c; } template <class T> inline T readInt() { int s = 1, c = readChar(); T x = 0; if (c == '-') s = -1, c = getChar(); while ('0' <= c && c <= '9') x = x * 10 + c - '0', c = getChar(); return s == 1 ? x : -x; } inline int64 readInt64() { int s = 1, c = readChar(); int64 x = 0; if (c == '-') s = -1, c = getChar(); while ('0' <= c && c <= '9') x = x * 10 + c - '0', c = getChar(); return s == 1 ? x : -x; } /** Write */ static int write_pos = 0; static char write_buf[buf_size]; inline void writeChar(int x) { if (write_pos == buf_size) fwrite(write_buf, 1, buf_size, stdout), write_pos = 0; write_buf[write_pos++] = x; } inline void flush() { if (write_pos) fwrite(write_buf, 1, write_pos, stdout), write_pos = 0; } template <class T> inline void writeInt(T x) { if (x < 0) writeChar('-'), x = -x; char s[24]; int n = 0; while (x || !n) s[n++] = '0' + x % 10, x /= 10; while (n--) writeChar(s[n]); } inline void writeInt64(int64 x) { if (x < 0) writeChar('-'), x = -x; char s[24]; int n = 0; while (x || !n) s[n++] = '0' + x % 10, x /= 10; while (n--) writeChar(s[n]); } inline void writeWord(const char *s) { while (*s) writeChar(*s++); } struct edge { int v1; int v2; }; struct ask { int l; int r; int v1; int v2; int ptr; int dp_order_l; int dp_order_r; bool answer; }; bool cmp_order(const ask &a, const ask &b) { return a.dp_order_r < b.dp_order_r; } bool cmp_answer(const ask &a, const ask &b) { return a.ptr < b.ptr; } int n, m, q; int lasts[MAX_M][2]; int size_of_lasts[MAX_M]; int need_ptr[MAX_M]; edge edges[MAX_M]; ask asks[MAX_Q]; vector<int> last_of_v[MAX_N]; bitset<MAX_M>* dp[MAX_M]; int main() { //freopen("input.txt", "r", stdin); //freopen("output.txt", "w", stdout); n = readInt(); m = readInt(); q = readInt(); memset(size_of_lasts, 0, sizeof(size_of_lasts)); for (int i = 0; i < m; ++i) { edges[i].v1 = readInt() - 1; edges[i].v2 = readInt() - 1; if (!last_of_v[edges[i].v1].empty()) { lasts[i][size_of_lasts[i]++] = last_of_v[edges[i].v1].back(); } if (!last_of_v[edges[i].v2].empty()) { lasts[i][size_of_lasts[i]++] = last_of_v[edges[i].v2].back(); } last_of_v[edges[i].v1].push_back(i); last_of_v[edges[i].v2].push_back(i); } for (int i = 0; i < q; ++i) { asks[i].l = readInt() - 1; asks[i].r = readInt() - 1; asks[i].v1 = readInt() - 1; asks[i].v2 = readInt() - 1; asks[i].answer = false; asks[i].dp_order_l = asks[i].dp_order_r = -1; asks[i].ptr = i; } int l, r; for (int i = 0; i < q; ++i) { l = lower_bound(last_of_v[asks[i].v1].begin(), last_of_v[asks[i].v1].end(), asks[i].l) - last_of_v[asks[i].v1].begin(); r = upper_bound(last_of_v[asks[i].v2].begin(), last_of_v[asks[i].v2].end(), asks[i].r) - last_of_v[asks[i].v2].begin(); if (l != last_of_v[asks[i].v1].size() && r != 0) { asks[i].dp_order_l = last_of_v[asks[i].v1][l]; asks[i].dp_order_r = last_of_v[asks[i].v2][r - 1]; } } sort(asks, asks + q, cmp_order); memset(need_ptr, 0, sizeof(need_ptr)); for (int i = 0; i < m; ++i) { for (int j = 0; j < size_of_lasts[i]; ++j) { ++need_ptr[lasts[i][j]]; } } int ptr = 0; for (int i = 0; i < m; ++i) { dp[i] = new bitset<MAX_M>; for (int j = 0; j < size_of_lasts[i]; ++j) { (*dp[i]) |= (*dp[lasts[i][j]]); --need_ptr[lasts[i][j]]; if (need_ptr[lasts[i][j]] == 0) { delete dp[lasts[i][j]]; } } (*dp[i])[i] = true; while (ptr < q && asks[ptr].dp_order_r < i) { ++ptr; } while (ptr < q && asks[ptr].dp_order_r == i) { asks[ptr].answer = (*dp[asks[ptr].dp_order_r])[asks[ptr].dp_order_l]; ++ptr; } if (need_ptr[i] == 0) { delete dp[i]; } } sort(asks, asks + q, cmp_answer); for (int i = 0; i < q; ++i) { ((asks[i].answer) ? writeWord("Yes\n") : writeWord("No\n")); } flush(); fclose(stdin); fclose(stdout); return 0; }

// Copyright (C) 2016 Sayutin Dmitry. // // This program is free software; you can redistribute it and/or // modify it under the terms of the GNU General Public License as // published by the Free Software Foundation; version 3 // This program is distributed in the hope that it will be useful, // but WITHOUT ANY WARRANTY; without even the implied warranty of // MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the // GNU General Public License for more details. // You should have received a copy of the GNU General Public License // along with this program; If not, see <http://www.gnu.org/licenses/>. #include <iostream> #include <vector> #include <stdint.h> #include <algorithm> #include <set> #include <map> #include <array> #include <queue> #include <stack> #include <functional> #include <utility> #include <string> #include <assert.h> #include <iterator> using std::cin; using std::cout; using std::cerr; using std::vector; using std::map; using std::array; using std::set; using std::string; using std::pair; using std::make_pair; using std::min; using std::abs; using std::max; using std::sort; using std::generate; using std::min_element; using std::max_element; template <typename T> T input() { T res; cin >> res; return res; } #define BASE 7 vector<char> get_digits(size_t v, size_t len) { vector<char> res(len); for (size_t i = 0; i != len; ++i, v /= BASE) res[len - 1 - i] = v % BASE; return res; } size_t A[2 * BASE + 2][2 * BASE + 2]; void precalc_a() { for (size_t n = 0; n != 2 * BASE + 2; ++n) for (size_t k = 0; k != 2 * BASE + 2; ++k) { if (k == 0) A[n][k] = 1; else if (k > n) A[n][k] = 0; else A[n][k] = (A[n - 1][k - 1] * n); } } vector<char> range(size_t a, size_t b) { vector<char> res(b - a); std::iota(res.begin(), res.end(), a); return std::move(res); } int main() { std::iostream::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); precalc_a(); size_t n, m; cin >> n >> m; size_t len1 = 1, len2 = 1; for (size_t a = BASE; a < n; a *= BASE) len1 += 1; for (size_t b = BASE; b < m; b *= BASE) len2 += 1; vector<char> dig1 = get_digits(n - 1, len1); vector<char> dig2 = get_digits(m - 1, len2); vector<char> used(BASE + 2, false); size_t ans = 0; for (size_t pref1 = 0; pref1 <= len1; ++pref1) { vector<char> nused = used; vector<char> last1 = (pref1 == len1 ? range(BASE, BASE + 1) : range(0, dig1[pref1])); for (size_t pref2 = 0; pref2 <= len2; ++pref2) { vector<char> last2 = (pref2 == len2 ? range(BASE + 1, BASE + 2) : range(0, dig2[pref2])); size_t mult = 0; for (char ch1: last1) for (char ch2: last2) if (ch1 != ch2 and not nused[ch1] and not nused[ch2]) ++mult; size_t left = len1 + len2 - pref1 - pref2; size_t hasdigs = std::count(nused.begin(), nused.begin() + BASE, false); hasdigs -= (pref1 != len1) + (pref2 != len2); left -= (pref1 != len1) + (pref2 != len2); if (left < 2 * BASE + 2) ans += mult * A[hasdigs][left]; if (pref2 != len2) { if (nused[dig2[pref2]]) break; nused[dig2[pref2]] = true; } } if (pref1 != len1) { if (used[dig1[pref1]]) break; used[dig1[pref1]] = true; } } cout << ans << "\n"; return 0; }

in DIV2, Problem D:Kay and Snowflake what i did was: 1.) Calculated subtree size for each node. And found parent for each node,stored them in an array. 2.) for query of node U ,i calculated the node with minimum subtree_size amongst those nodes(v) in subtree of U which have subtree_size(v) > (1/2)*subtree_size(U). But i faced TLE. And henceforth answer is the node satisfying the above condition. Please help me out i i can improve my complexity. THANKS IN ADVANCE

Comments (116)

Show archived | Write comment?

Errichto

8 years ago, # |

← Rev. 2 →

In 685D - Кай и вечность we can achieve shorter implementation using set from STL. My solution is similar to the one from editorial, but I have set with numbers +1 and -1, instead of a segment tree. I use the fact that iterating over set takes O(size), not O(size·log). Check details in my code. To store +1 and -1 sorted by y, I represented +1 by 2y and -1 by 2y + 1. This way, I don't need to store pairs, what would be slightly slower (and maybe it would give TLE).

code for D

#include<bits/stdc++.h>
using namespace std;

long long ans[1005 * 1005];

int main() {
	int n, k;
	scanf("%d%d", &n, &k);
	vector<vector<int>> w;
	for(int i = 0; i < n; ++i) {
		int x, y;
		scanf("%d%d", &x, &y);
		w.push_back(vector<int>{x-k, y, 101});
		w.push_back(vector<int>{x, y, 102});
	}
	sort(w.begin(), w.end());
	multiset<int> s;
	int x_prev = -42;
	for(vector<int> & event : w) {
		int x = event[0];
		if(!s.empty() && x_prev != x) {
			int mul = x - x_prev;
			assert(mul > 0);
			int y_prev = -42;
			int cnt = 0;
			for(int y : s) {
				assert(cnt >= 0);
				if(cnt) ans[cnt] += (y/2 - y_prev) * mul;
				if(y%2) --cnt;
				else ++cnt;
				y_prev = y / 2;
			}
		}
		int y = event[1];
		int type = event[2];
		
		if(type == 101) {
			s.insert(2 * (y - k));
			s.insert(2 * (y) + (y >= 0 ? 1 : -1));
		}
		else {
			s.erase(s.find(2 * (y - k)));
			s.erase(s.find(2 * (y) + (y >= 0 ? 1 : -1)));
		}
		
		x_prev = x;
	}
	for(int i = 1; i <= n; ++i) printf("%lld ", ans[i]);
	puts("");
	return 0;
}

Oh, so O(nm) wasn't intended in 685D - Кай и вечность. I'm surprised. Constraints and everything looked like it's what organizers wanted. Anyway, it didn't spoil a problem I think (though it made it easier). By the way, did you think that O(nm) won't pass or you didn't come up with this solution?

→ Reply

ch_egor

8 years ago, # ^ |

We want to cut off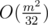 $\text{[math]}$ solution. On this limits difference in TL near 3. But we write very unoptimal O(nm) solution and didn't know that it can pass.

riadwaw

Just wondering what was the difference in time between main solution and nm solution. Was it really at least 4 times?

cdkrot

It was.

It seems, than nm solution runned too slowly because of cache: my code was iterating over first dim of matrix, and it is not good.

I was making scanline from left to right, and the right to left is better.

Just reversing everything makes it run over second dim of matrix, as in Ac-ed solutions.

I've written it, but it turned out, that implementation wasn't effecient enough.

Actually the most effort was made to cut O(M² / 32) solution (however it has pretty simple and nice idea beneath it).

It was hard to cut it, and this way I accidently opened door to O(nm) solution.

uhateme

Can u share idea behind O(M^2 / 32) solution too?

← Rev. 3 →

Solution in M² / 32, for div1.E.

Let's create a matrix of N x M size and create a graph node from each cell.

{We will not use it in final code, but it is important for explanations}

Let's add some edges in this graph:
* (w, i) -> (w, i + 1) for all i, w
* (v_i, i) -> (u_i, i) for all i
* (u_i, i) -> (v_i, i) for all i

v_i, u_i — are endpoints of i-th edge.

How to answer on query L, R, S->T? We just need to check, that there is a path from (S, L) to (T, R)

However N x M table is too big for us, let's shrink it.

Take note, that it is enough to check reachability within (S, L') and (T, R'), where L' — smallest num, with L' ≥ L and (U_L' = S or V_L' = S) Аnd R' — been the biggest number, with R' ≤ R and (U_R' = T or V_R' = T)

This way almost all vertexes can be eliminated from graph, they simply will not be used. It is enough to create a new copy of vertex only when it was mentioned in new edge.

Also, we were adding this edges before: (u_i, i) <-> (v_i, i).
We will compress this two vertexes into one, since the relations of reachability are same for them

After following operation we have acyclic graph with M vertexes and O(M) edges.

We can calculate the following dp on it:

dp[v] — is bitset of reachable vertexes (vertexes of our supplementary graph).

And so complexity is M² / 32 for both memory and time.

However memory complexity can be boosted (thanks to ch_egor):

You can go with scanline over edges, answering queries in certain places.

Quite often some state of dp will be not used till the end, so it can be destructed to rescue memory for next ones.

My code (but without memory optimization)

Спойлер

ch_egor's code (memory optimization + dirt optimizations like fast io).

dhawalupadhyay

Can you explain the O(nm) solution for Div-1 E.

+10

Go with scanline from right to left, and maintain following dp:

dp[i][j] -- if L is current pos of scannline, the smallest R, which makes possible to go from i to j.

While you go with scanline add edges to this dynamics (requires recalculating O(N) values), and answer the queries, when current position of scannline coincides with querie's L.

fofao_funk

Why is the complexity of Div1B's second approach O(N * log²(N) + Q)? I know one of the log factors is due to the set usage; but why does the merging step also have O(log(N)) complexity? Shouldn't it be more?

It is a common trick with merging sets.

Let's always merge smaller set into larger, this way when element is merged from one set to another the size of the set in which it lives doubles at least.

Hence each element will not be moved more, than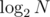 $\text{[math]}$ times.

Omar_Mekkawy

How come it doubles at least? and what do you mean by the set which it "lives" would you clarify more please?

The key idea is following: each elements starts in it's own std::set, and sometimes we ask sets to merge together.

How to merge them? Select smaller set and add all those elements to larger set.

Notice, that each time some element changes set, the set in which it lives grows at least two times (since large set ≥ smaller).

Hence, there can't be more than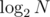 $\text{[math]}$ movements per element.

If you need more info, read 600E - Lomsat gelral and it's editorial.

Got it thank you <3

Swistakk

+67

Lol, you considered O(nm) as bruteforce and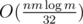 $\text{[math]}$ as a model solution :|? Do you know that dividing as 32 in the most typical model of computations is in fact dividing by log :)? And in reality, not in plain theory, isn't that still more or less the same? There is no reason to apologise that O(nm) passed, because I doubt it is possible to make a distinction between those 2 solutions.

kalimm

+112

In Balkan OI 2014, there was a problem with N≤10000 and intended solution was N * log(N) + N². Author of problem apologized after contest because of there are some AC with N² + N².

This is even funnier than it.

P___

Well — even though this is a programming contest, I think that the solution should focus on pure big O complexity.

In this contest the model solution was O(nm log m) -> there is no O((nmlogm)/32) complexity.

In case of Balkan OI the model solution was O(N^2). I don't understand apologizing for letting the solutions with the same or better big O complexity get AC.

Furthermore I would be surprised if the O(nm) or O(N^2) solution didn't AC.

Dividing by 32 can be a nice trick if your big O complexity is worse than the model one and you used that trick to speed up things a bit. That trick should never be required by the model solution.

I hope you may change your mind if you read my comment below.

desert97

+36

I find O(stuff / 32) problems pretty dissatisfying in general. I personally don't find it interesting at all that you can speed up a problem by a factor of 32 or 64, and that this often constitutes the "main difficulty" in a problem.

+44

There was a time when I had a similar opinion as yours, but after I realized what this "/32" in fact really is, I think it is perfectly fine.

Do you agree that we should be able to handle "a+b" operation in constant time? If we won't, because a and b binary notations are of logarithmic length, hence this operation requires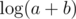 $\text{[math]}$ operations then in 99% of problems we should put additional 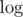$\text{[math]}$ into complexity, because summed length of bits sequences we are dealing with is (previous complexity) 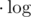$\text{[math]}$ . It would be rather inconvenient to put additional 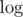$\text{[math]}$ into complexities almost everywhere, because of arithmetic operations. Moreover that suits practical model, because as long as we are dealing with numbers from not very large range we perform arithmetic operations on bits sequences not longer than 64 as fast as we perform operations on shorter sequences and only reasonable way of extending that arrangement to arbitrarily large integers is to assume that we are able to perform operations on bits sequences of length 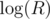$\text{[math]}$ in constant time (where R is range of numbers on input). Either we accept it as a fact that we are able to do this or we demand adding two numbers to take logarithmic time. There is no way to "ban cheating with dividing by 32" and have constant time addition. Thus, consequence of having addition in constant time is being able to perform operations on bits sequence of logarithmic length in constant time, because constant time addition is same kind of cheat as ability to xor sequences of length k in k/log k time. That enables you to sometimes perform operations on data of O(n) size in 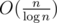$\text{[math]}$ time which is for example a state of an art algorithm for transitive closure.

tl;dr dividing by 32 is not optimization by a constant factor, it is optimization by a logarithmic factor Because of that I definitely don't consider such solutions as dirty tricks.

ok ok I had something here but then I understood what you're saying. That's reasonable. Further question: what do you think about the following problem that I might use on a future contest. You have 10⁵ integers, each of size ≤ 10¹⁰⁰⁰⁰. Find their sum and print it out.

(ok the future contest part is a joke)

Hm, yeah, I guess you didn't get my point :P. We are considering theoretical model. Do you want to multiply complexity of 99% of your solutions (those requiring any arithmetic operations) by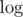 $\text{[math]}$ factor coming from arithmetic operations? I guess no. If we stick to computations performed on a modern computer, following your reasoning, why do you write that algorithm of adding n numbers not larger than R is O(n), but not 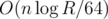$\text{[math]}$ ? Bits notations of such numbers are of length 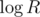$\text{[math]}$ and you are not able to shave off log factor, just 64 one. You may didn't realize this, but model when we are able to perform whole 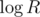$\text{[math]}$ factor is exactly the model whole CF community communicates within. If you accept algorithm of adding n numbers from range R to be O(n) then you also accept 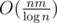$\text{[math]}$ algorithm to transitive closure. 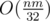$\text{[math]}$ algorithm is in fact a better complexity, because it translates to 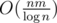$\text{[math]}$ in a theoretical model and fact that we need replace that log with 32 is only a technical barrier. I have a feeling that I am saying the same statements over and over and can't explain it much better :).

EDIT: Oh, I see you changed your comment while I was writing this :).

EDIT2: Regarding to your further question. I have to admit that I am not fully sure whether R I used so far should denote range of numbers we are dealing with. Maybe it should denote length of input or sth, but I am not sure right now.

Oh, for transitive closure, you can do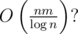 $\text{[math]}$ This is really surprising to me, as I thought the best savings you get in all cases is 64 or something (for all problems of this type).

haleyk100198

-8

Same here. I was just scan-reading the tutorial for a hint and the first thing I see is to iterate all n and m. I got an AC for iterating through all value of n and m, and I didn't even store the representation of values <m. Pretty sure this is not a worthy solution.

*whoops, wrong topic.

derAdler

can anyone plz explain the duv2D 3rd solution by ch_egor, what does big_subtree[] stand for and what is dfs_centroid calculating

The idea is that say the node u has more than one child and heaviest one is v, and say the centroid of v is vc, then the centroid of u will be on the way from vc towards the root. For leaf nodes, centroid are themselves, and for others, consider the lifting model, thus complexity being O(n) only.

shubhamgoyal__

Hi, Can u plz explain this->"heaviest one is v, and say the centroid of v is vc, then the centroid of u will be on the way from vc towards the root". Thanks.

szawinis

Correct me if I'm wrong, but is the centroid of u either itself or vc? And is that why the complexity is O(n)? Thanks in advance.

mishraiiit

You are wrong. The centroid is either u or some vertex beetween u and vc.

The amortized complexity is O(n). Think of it like, at every node, we do some lifting, lifting from centroid of big subtree (vc) to some nodes up (nvc : which will be the new centroid) . Now let's say you lift vc up to node nvc. Let's say the path is vc, parent[vc], parent[parent[vc]], ..... nvc.

You will notice that for all nodes, these paths are disjoint. So this extra loop inside every node for lifting will be O(n) for all nodes combined.

Sadia_Atique

I used almost similar idea, but instead of lifting up, I was trying to lift down. I start from the top of the tree, and find centroid for each node. For a node u, if it's parent's centroid c is in u's subtree, I try to lift down from c until I find the centroid, if c is not in u's subtree, I start searching from u node itself. The logic behind this is if u is the heavy child of it's parent, it must have it's parent's centroid in it's subtree, thus avoiding some steps and jumping directly to the centroid node for search. If u is not the heavy node, it's subtree is being explored for the first time, so it's not repeating. I got tle in 14th test case, can someone kindly point out my mistake here?

http://mirror.codeforces.com/contest/685/submission/18730022

Your mistake here.

Code

bool isCentroid(int root, int center){

	int i,child;
	if( (sub[root]-sub[center]) > (sub[root]/2) )  return false;

	for(i=0; i<adj[center].size(); i++){
		child = adj[center][i];
		if(sub[child] > (sub[root]/2))  return false;
	}

	return true;
}

You check every vertex in O(deg(c)). 14th test looks like bamboo with tall $\text{[math]}$ and sunshine with size $\text{[math]}$ . The main vertex of sunshine is centroid of $\text{[math]}$ subtrees, because this your code works in $\text{[math]}$ .

TerryMcGinnis

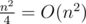While I drew diagrams and wrote equations for subtree sizes for certain cases to prove ch_egor's solution in the middle of the contest (and it passed :D), could someone give me a general, more formal proof for it?

Tiny

consider vertex u, let v be the maxSize Child of u, let w be centroid of v, go along path from w to u, there are 2 case 1. size(v)<=size(u)/2, u itself is centroid of u. 2. size(v)>size(u)/2, along the path from w to v, the first vertex x satisfying the condition (size(x)>=size(u)/2) is centroid of u, such x must exist as x=v satisfy the condition. let prove case 2, x must be a centroid of u. if x=w, obviously true; if x!=w, let y be the preceding vectex of x along the path(y is a child of x), there are 3 types of components, 1.subtree(u) — subtree(x), obviously ok as sizeof(x)>=size(u)/2. 2.subtree(y), ok because size(y)<size(u)/2, otherwise the first vertex satisfying the condition will be y or some preceding vertex instead of x. 3.subtree(z) (z != y && z is a child of x), size(z) < size(v) — size(w) <= size(v)/2 < size(u)/2, ok

hello friends i wrote a coded up the div2 c problem and it is giving wrong answer on only two test cases(and possibly more not included in the test case file) could someone plz check what is wrong with the code it's simple recursion, here is the link code: http://mirror.codeforces.com/contest/685/submission/18694520. As you could clearly see in the code i cheated(of course i couldn't get it to submit during contest)...so plz help!!! i would be really grateful if someone could tell me what is wrong with the solution.

mathusalen

It is curious because I compiled and ran your code locally removing the "cheating part" it works perfectly well in the two problematic test cases but if we check it on the server of codeforces it gives WA.

I see now, the problem is with the function pow. It is defined for doubles and you are using for ints. Small roundoff errors give you trouble. It is better to implement your own powq function as in

code

long long powq (long long a,long long b) {
  long long res=1;
  while (b)
  {
      if (b % 2) { res = (res * a); }
      a = (a * a);
      b /= 2;
  }
  return res;
}

Then it works properly

can the centroid for a vertex lie above a vertex v if yes then how (are we then considering the whole tree or just the subtree of a vertex) and how can we prove this model.

The centroid of subtree at vertex v must be one of its children. Have a look at the problem statement ;)

fetetriste

Div1 C is a harder version of GCJ 2008 R2 Problem C — Star Wars: https://code.google.com/codejam/contest/32001/dashboard#s=a&a=2

LeBronJamez

An other solution for Div2 D/Div1 B: The algorithm for finding the centroid of a general tree is the following: If we are currently at node u and we are looking for the centroid, we find a child v of u with size[v] > N/2 and continue our search for the centroid from v. Now let us for every node u create a path containing all the nodes we have selected with this process. We have just done Heavy-Light decomposition to our tree, and every path we have created is a heavy path. So, when we want to find the centroid of the tree rooted at a node r, we can find it with a simple binary search in the heavy path which contains r. (Solving the problem with this method doesn't require knowledge of Heavy-Light Decomposition though) Code

voz.beginner

Nice! Got accepted using your approach, thanks bro.

You are welcome :)

mdtareque

Can anyone please shed light on below line of code from Problem C editorial solution? How is this checking for unique combinations?

   if (*std::max_element(used.begin(), used.end()) <= 1)
      ++ans;

used[v] = how much times this digit occured.

If all digits occured no more than once, than this time all digits were distinct.

FundamentalEq

max_element(used.begin(),used.end()) returns the iterator to the maximum element . We are checking if the value of the maximum element <= 1 . If there are any repetition the value of the maximum element >=2 else there are no repetition .

pH7

How can Div2C be solved when Base( <= 10^9 ) is not fixed ?

Hint: solve in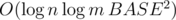 $\text{[math]}$ first.

Hey, i could think of a dp solution. Not so sure about complexity. Please check it 18702275

Your complexity looks like O(BASE² 2^BASE).

I am still confused about the complexity part ! But at least now, can you share how to solve it in O(logN * logM) ?

I can share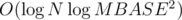 $\text{[math]}$ solution, I see ways to boost it (Drop base² from complexity in trade of to more $\text{[math]}$ 's), still i don't want to implement this.

The basic idea is that you bruteforce the common prefix of max hour and target, and same for minutes.

When you fixed common prefix and first digit after it you just use combinatorics formula.

P.S. This code can be used with different bases, however some things might be needed to adjust, e.g to avoid overflows.

Tanks for answer, I'm so busy these days.

Thank you. Both ! Maintain this generosity even when you're red :) And i like coordination between you two !

thank you :)

rhezo

In DIV2D, "We write the euler tour of tree and we will use a 2D segment tree in order to search for a vertex quickly. ". How to do a query? Also please tell the properties of euler tour too.

Write the euler tour of tree, subtree of v_i now takes some contigious segment of the tour.

Select from this segment minimum number greater or equal to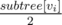 $\text{[math]}$ , why this works is explained in editorial.

So you want to perform queries with three params: L, R, C — you can do this with 2d segment tree.

After we do the euler tour, each subtree becomes a subarray, right? Are they also ordered by some property like increasing subtree sizes? Or random?

If they are random, I don't understand how we could use a 2D segment tree to find a number greater than X/2 in some subarray. Please give more details :)

Each subtree becomes an subarray, yes. You should write to the array the subtree sizes of vertexes.

Yes, numbers are not sorted within given subarray, so 2d tree come to help.

You can create segment tree, where each node contains sorted array of values of all leaves it contains. It can be done in $\text{[math]}$ time. Note, than each element lives in $\text{[math]}$ elements, so this is why it is $\text{[math]}$ , not more.

Using this segment tree is easy: you split your request to list of nodes as usual, and in each node you make a binary search.

Thanks, that clears it up. Will try to implement it!

I got AC using this idea, thanks! Can you explain the second approach in a little more detail? What is "merging sets" idea?

+11

It is a common idea.

Checkout this problem 600E - Lomsat gelral and this editorial for it.

ps06756

In each node of segment tree, are we storing a sorted array of that range and then using binary search to search for the value just greater than (subtree_size/2) ? If yes, then won't the cost of constructing such segment tree be O(n^{2}) ?

Do you know that merging two sorted arrays into one new can be done in O(len_of_first + len_of_second)? It is a key idea to know, may be you have encountered it before in mergesort algorithm. It is also implemented in c++ as std::merge.

How to construct such tree? Construct it recursively: at first construct child nodes with same constructing function, and then merge sorted arrays of left and right nodes into array of this node.

Why this is O(N log N)? Your recursion will have O(log) levels of recursion, and you will have O(N) work done on each level (it is same as in merge sort).

Thanks @cdkrot, I calculated the complexity in a wrong way and that's why was confused.

Knight_of_Thirteen

Can anyone tell me that how can I reduce complexity of my code for Div2D? I am not quite sure what's the complexity here :( Thnx in advance.

My code: http://pastebin.com/HJNpnwyq

abdullah_alperen

If I am not mistaken, you firstly check a node's heaviest child whether it is the centroid. If not, then you go down on the tree until you find it. However, it is not what is told in the tutorial and has a complexity of O(N^2). To make it correct, initialize your par variable with the centroid of your heaviest child and climb the tree upward by going to one's dad in each step. Please let me know if you need any further explaination :)

shivang_bansal

Can anyone please explain the Div2 C. Robbers' watch problem. I am not able to understand the problem statement clearly and how is the pigeonhole principle appyling in the solution. Please help. Thanks in advance.

seeker

(Refer the problem statement for terminology) Suppose there are h places for display in hour section and m places for minute section. Now, problem says that all digits in hour and minute section taken together should be distinct. Since, its septimal number system, so possible digits are 0,1,2,3,4,5,6, i.e. 7 distinct digits. So, if sum of places in hour and minute section is greater than 7 then it is impossible that all the digits are distinct because we have 7 digits available and places are more than 7.So, the answer should be zero in that case. This logic is formally called pigeonhole principle.

For cases when total available places in hour and minute section are less than or equal to 7, we apply brute force approach. that is we take every possible value for hour(0 to n-1) and minute (0 to m-1), then convert them to base 7 and see if all digits are distinct are not. For this you can use an array for digits 0 to 6 and track the count of every digit while converting hour and minute to base 7. If any digit's count is greater than 1, then that combination of hour and minute is rejected.

Hi, thanks for the explanation, I have understood the problem and Pigeonhole principle and although one thing still confusing me is that->

why do we need to track the count of every digit while converting to base 7, I mean why combination is rejected if the digit count exceeds 1. I know maybe I am asking very basic question. Sorry for inconvenience :)

Because the problem asks to find all those possible combination of hour and minute such that no digit appears more than once in the whole clock display. For eg, 02:23 (hr:min format) is not allowed since 2 appears more than once.

Oh yes my bad, that was really easy :P

Anyways Thank you very much for your help :)

Mr.Awesome

I'm wondering how to solve div2/B if we have to minimize the number of operations ?

rajpm

In DIV-2 D/DIV-1 B , the last solution taking O(n+q) time complexity to solve uses the line "Note that the centroid of the child after a certain lifting goes into our centroid. Let's model the lifting. ", for explanation which I am not able to understand, could someone please explain what is the lifting operation mentioned here and how is it helping ?

Mucosolvan

I'll copy paste my explanation, ask more if you need anything: Of course, the centroid of the leaf is the leaf itself.

What about the node?

Let's find the size of every subtree.

If for every node's child it's (child) subtree size <= size(node) / 2 than the node is the centroid.

If not, then centroid of node is the children's centroid. It only fails one kind of test — where the path from the node to the centroid is longer than size(node)/2, then we have to find a node that is an ancestor(parent or parent's parent etc) of the centroid, that will be good for our node.

The node has to be on the path from the centroid to our node. Why? Let's try a node that's below the centroid — then the size of our component is even bigger.

So let's take another node that is above our centroid but not on the path between them. Then we have a component of size at least n/2, because if it wasn't, then we would've had another centroid computed for our son by that time. Try to draw a picture and it should be intuitive why it's that way.

Thanks for the reply, consider this example https://postimg.org/image/9v9wg9idt/ the centroid of the node (u) passes the test you mentioned bcoz it is at length 3 which is less than size(node)/2 but we will still need to find some ancestor as it is not the centroid of node (u) , but I think one way to quickly check if centroid of one of the child is centroid of the node as well is by checking the weight of centroid, it the weight of centroid is x then weight of the remaining part after removing it would be weight(node)-x-1, we can verify both the values and if they don't satisfy, we can look forward for ancestors. Also for the case in image the centroid of the node (u) would be v which is along the path from node to centroid, but still the centroid. Thanks again .

In our case v subtree is bigger than half of u subtree size, so v centroid is our candidate. We have to check if v is centroid of u, so check the length of the path between u and v, it is 1, which is less than size of u subtree, thus v is u centroid. If length of path from u to v was longer than u subtree size then you would have to iterate through v ancestors. Sorry for mistakes, writing on mobile

"So let's take another node that is above our centroid but not on the path between them. Then we have a component of size at least n/2, because if it wasn't, then we would've had another centroid computed for our son by that time. Try to draw a picture and it should be intuitive why it's that way." — This is the part that I cannot understand. Could you elaborate a little bit more? I'm sorry to pester you.

Sure, no problem! Imagine we're in vertex u, that has the child of size bigger than size(u)/2, let's name this child's as w and it's centroid as v. If v != w then we know, that v is in w subtree with size bigger than size(v)/2. Let's take vertex z that is not on the path between v and w and assume it's u centroid. Then there has to be a vertex c on that path that has both v and z as children in different subtrees (maybe not direct), but if v is w centroid, then it also has to be c centroid, so c subtree with v in it is bigger than size(c) > 2, so z cannot be a c centroid. Moreover, it cannot be u centroid. So we have a contradiction.

It isn't beautifully written, I can't really put it into words, if you have any more questions feel free to PM me

JEEADVANCED

4 years ago, # ^ |

Perfect!! 4 years old comment still helps!!. Thanks Mucosolvan

krishnkant_

My code 18714720

Your code's complexity is O(NQ), since you run dfs for each query.

You should write something more effiecient, reread the editorial.

P.S. It is old century to store graph in hand written lists, most people now use

vector<vector<int>> graph(n);
// graph[i] contains list of neighbours of i.

It's just more simple to write.

wrg0ababd

Can someone explain what std::move does in div 2 D solution with merging sets? How would this solution work without it?

dreamzor

In that particular code explicit std::move does nothing. I'd say it even makes things worse as it blocks potential Return Value Optimizations.

However, move semantics (which are triggered on return anyway without explicit std::move) allow not to copy the set on return, but move it cheaply — something like returning a pointer, but more convenient.

singh_iitian

Can someone explain how the time-complexity is O(n+q) in Div2D Kay and Snowflake third approach. I am unable to understand O(n) part due to the below code. I think in worst case, it will take steps equivalent to its height thus making complexity > O(n).

while (!is_centroid_of_subtree(v, c)) { c = prev_of[c]; }

Consider each edge. It has upper and lower ends. Lifting can be done only from lower to upper, and due to the DFS nature of solution it happens no more than once per edge.

And num of edges is O(N) (N - 1 to be precise).

loser21

For Div1 D, can someone explain this in more detail from the editorial : "Suppose we update the value of a cell on the row a, and before it was updated the value x on the row b. Let add to the answer for the number of squares containing x points value a - b."

Hello, I have tried solving Div2 D/ Div1 B by selecting a child vertex which has subtree size > (1/2)*total_subtree_size of that node, but I am getting wrong answer on 3rd testcase. Can someone please point out what am I doing wrong ?
Submission

komolakanto

subtree size should be >= not > than half of total_subtree_size. btw floor division's also a problem. look out for that one.

Agassaa

can anyone explain what " lifting " means in div2D editorial?

In this approache we choose centroid of the heaviest child. Then we are lifting it while considered vertex is not a centroid of subtree. In this case it means that we look at vertex if it is centroid of subtree do nothing else we look at parent of vertex. If parent of vertex is centroid do nothing else look at parent of parent... Do this while considered vertex is not centroid of subtree.

gabrielsimoes

What is "manhattan distance <= const" equation? Wouldn't that be |x2 - x1| + |y1 - y1| + |z2 - z1| ≤ const ?

Yes it is. One of (x_1, y_1, z_1), (x_2, y_2, z_2) is target point you are trying to find, and the other is source point given in test.

Const is equal to mid value from binary search.

mshcherba

What is v in 686E - Оптимальная точка and what does v = 10 * * 18 mean? Thank you.

v means bounds of coordinate. 10 * * 18 is mistake, it means 10¹⁸. I fixed it now.

Could anyone explain how do we do binary search in 686E - Оптимальная точка?

Consider boolean function f(L) -- is there a point, which makes answer not worse, than L?

We are searching for lowest x, such that f(x) = 1. Using binary search.

sanket407

Why do you add +1 when calculation first of a',b',c' in "tr.c.first = DIV2(tr.c.first — r + 1);" ??

Also in get_solution can you explain the final calculation part using delta ?? Couldnt get the logic .. Seems mathematical

Because we need to round in different ways. In one case we want to round down ("floor"), and in other case up ("ceil")

Let me explain using example. Consider following inequality, solve in integers.

a ≤ 2x ≤ b

Since x is integer, we transform:

$\text{[math]}$

And ceil operation can be written as floor operation:

Also take note, that we don't divide using divide operator, it rounds toward zero, which is not good for us.

ok ! Also explain the final point calculation using delta

At first we make some comparisons, to make sure, that solution exists.

After that we generate one of solutions. At first we take a, b, c at their minimum. However their sum can be too small, in this case we want it to be raised to minimum S.

So we calculate delta -- how much we need to raise, and then we raise in such manner, that a, b, c will never be more, than maximum.

Thanks a lot mate ! Got it Accepted !

One last thing : That div2 function will make difference when dividing by 2 and taking floor of negative nos. right ?

As -3/2 = -1 but div2(-3) = -2

Yes, exactly. Div2 func always rounds down. Which matters for negative odds.

How do we count f(x)?

Mentioned function is simple boolean function -- have we such point or not?

I believe, that this function is explained in editorial thoroughly. Try reading it again.

If it will not help -- send me a PM.

petil777

In cdkrot code.... Is "std :: merge" working in the way smaller one attach to larger one? (O(logN))? I mean, std::merge(sm.begin(), sm.end(), big.begin(), big.end(), vec.begin(), vec.begin()) --> this will be sm---(attach)-->big and copied to vec?

And I think copying time is somewhat costly isn't it?

There are two solutions by me for centroids problem.

One uses 2d segment tree, and other uses merging sets.

std::merge is used in 2d segment tree solution, if you want merging sets solution, check the other code. (it contains the word "set" in the code).

Thanks for comment in person. After read all of solutions carefully for Div2-D, O(n+q) solution was what I really want. One of my goal was to solve like this kind of problem(which requires some sense and proof). But when solving problem D of any Div2, I failed 50% of them (like in this case...) The common point of failing (I think) is not how to prove but how to come up with "idea" (In this case, centroid of u must be on the line of centroid of v to u, v is child of u who makes sub[v]*2>=sub[u]). Could you give me any advice for accessing this kind of problems or training this kind?

Don't know, really.

May be you need to get more experience -- then write more contests. May be you need theory. May be something else...

If you have opportunity to ask coach for help, than you should do it.

cerberus97

In Div 2 E (Optimal Point), the editorial says:-

2) Consider areas of "good" points (with dist ≤ mid) for each source point.

What is mid here?

If you know what binary search is, it should be obvious.

If you don't know what binary search is, then you should learn it.

So what are L and R here?

Do you know what the binary search is?

Yes.

I apologize for bothering you. I was a bit confused by the editorial. After reading this editorial for a similar problem, I now understand the solution.

Not a problem, feel free to ask.

WyldeCat

Can someone explain how to solve div2/E (Optimal point) with ternary search?

Thanks.

Edgedancer

5 years ago, # |

Can someone explain how to solve Div 1 A in O(log n log m)

ch_egor's blog