Задача 192A - Модные числа
Кратко о решении: перебор
Подробно о решении: Нетрудно заметить, что это числа положительны, следовательно каждое из слагаемых меньше N. То есть всего различных возможных слагаемых порядка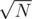 
. Это значит то, что мы взять и одно из слагаемых перебрать. Тогда нам нужно научиться проверять, является ли какое-то число треугольным. Заметим, что если мы заранее выпишем все слагаемые в порядке увеличения то мы сможем с помощью бинарного поиска в массиве искать наше число. Это даем там решение за 
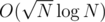. Если перебирать первое слагаемое в порядке увеличения, то можно использовать два указателя, что дает нам решение за 
.
Задача 192B - Прогулки под дождем
Кратко о решении: динамика.
Подробно о решении: динамика d[i] — количество дней, в течении которых плитка номер i доступна. Пересчет: d[i] = min(a[i], max(d[i - 1], d[i - 2]))
Асимптотика решения: O(N)
Задача 191A - Династические головоломки
Кратко о решении: динамика
Подробно о решении: динамика d[i][j], i — первый символ в имени династии, j — последний текущий символ. d[i][j] — максимальная текущая длина. Переход: для слова с первой буквой l, последней буквой r и длиной s для всех возможных первых букв i состояние d[i][r] может быть улучшено значением d[i][l] + s.
Ответом будет являться максимальное значение d[i][i] для всех i.
Асимптотика решения: O(N * alpha), где alpha — это размер алфавита.
Задача 191B - Митинг
Кратко о решении: конструктив
Подробно о решении: заметим, что на последнюю площадь никогда не выгодно подавать заявку (денег мэрии не потратим, ничего не изменится, мы просто потеряем ход). Переберем площадь, на которой мы хотим провести митинг. У нас есть k - 1 ход на то, чтобы потратить деньги мэрии (один ход нам нужен на подачу заявки на искомую площадь). Тратить деньги выгоднее всего на самых дорогих площадях, за исключением последней. Осталось научиться быстро выбирать k - 1 максимум из всего массива, за исключением данного элемента. Для этого сначала отсортируем массив и получим k максимумов (последнюю площадь мы не должны рассматривать). Проверяем, лежит ли наше текущее значение в k - 1 максимальных (бинпоиск и не только). Если лежит, то искомые k - 1 максимумов — это максимальные k элементов без нашего. Если не лежит, то это просто максимальные k элементов.
Теперь когда мы понимаем, сколько денег мэрии мы можем потратить, то тратим их и смотрим, остаются ли еще у мэрии деньги на проведение события на нашей текущей площади
Асимптотика решения: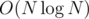 
Задача 191C - Дураки и дороги
Кратко о решении: lca
Подробно о решении: Разобьем каждый путь на два, строго идущих вверх к наименьшему общему предку. Теперь у нас есть только "вертикальные пути". Для каждой вершины насчитаем такую величину: количество вертикальных путей, начинающихся в ней минус количество вертикальных путей в ней заканчивающихся. Если мы насчитали эту величину, то ответ для ребра — это сумма значений в его поддереве. Насчитать такую величину довольно просто: берем для каждой пары дураков считаем lca этой пары. В города дураков прибавляем единичку, в lca значение уменьшаем на два.
Асимптотика решения: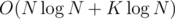 
Задача 191D - Схема метро
Кратко о решении: снова динамика
Подробно о решении: динамика d[v][rest][cycle] — количество линий, которое требуется для того, чтобы в поддереве вершины v все покрасить, в v остаются rest незамкнутым, cycle — правда ли, что нам надо обрабатывать цикл, в котором мы находимся.
Если мы находимся не в вершине цикла, то обрабатываем всех детей, говоря что мы хотим, чтобы в них было по одному незакрытому пути. Пусть у нас есть s сыновей, нам надо взять и замкнуть все лишние линии, а недостающие нагенерить. То есть ответ это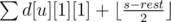 
, если s > rest, и 
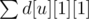в противном случае.
Если мы находимся в вершине цикла, то либо мы покрываем этот цикл кольцом и это стоит нам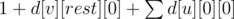 
, где u — это вершина на цикле. отличная от v. Другой вариант — покрыть все участки кольца радиальными линиями. Утверждение: это всегда можно оптимально сделать ровно двумя радиальными. Пусть это не так. Тогда рассмотрим некоторую вершину, в которой радиальные линии <<подвешиваются>> к кольцу. От неё по кольцу в разные стороны уходят два тоннеля, принадлежащие этим линиям. Так как различных линий на кольце сейчас не менее трех, то мы можем перенаправить радиальные линии следующим образом: соединить куски вне кольца друг с другом, а кольцо замкнуть. На кольце останется не менее двух кусков, следовательно все линии останутся валидными, а их число не изменится.
Теперь надо выбрать две станции, из поддерева которых будут выходить радиальные ветки, покрывшее кольцо. Стоимость такой станции это d[u][2][0], а обычной — d[u][0][0] (d[v][rest][0] в случае той вершины, которую мы сейчас обрабатываем) . Соответственно, нам надо выбрать две станции с максимальным значением d[u][2][0] - d[u][0][0].
Асимптотика решения: O(N)
Задача 191E - Разгон митингов
Кратко о решении: бинарный поиск по ответу
Подробно о решении: Сделаем бинарный поиск по ответу. Нам надо посчитать количество отрезков, на которых сумма больше нашего некоторого значения. Как мы это будем делать: будем обрабатывать все отрезки в порядке увеличения правых концов. Отрезки с одинаковыми правыми концами будем обрабатывать пачками. Более подробно: мы будем поддерживать некоторую структуру данных в которой будут храниться суммы всех отрезков c фиксированным правым концом.
Для того, чтобы быстро пересчитывать, нам нужно всего добавить в множество некоторый элемент ( 0, если точнее) и добавить ко всем элементам множества некоторое значение (a[i], если быть точнее). Еще нам нужно уметь отвечать на запрос <<количество элементов, больших данного на отрезке>>. Все это умеет быстро реализовывать, например, декартово дерево. Но нам придется дополнительно хранить некоторую величину X, означающую <<надо прибавить к элементу из декартова дерева X, чтобы получить реальное значение>>. Тогда при добавлении элемента a в нашу структуру надо будет положить в декартово дерево величину a - X, а прибавление некоторой величины ко всему множеству реализуется простым изменением X.
То есть у нас есть структура данных, которая умеет все эти операции выполнять за 
. То есть одна итерация внешнего бинпоиска работает за 
, следовательно весь алгоритм работает за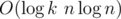 
Асимптотика решения: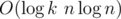
Можно просто для каждой вершины выписать, на каком она месте и бинпоиск не нужен.
Напишу и сюда тоже. В задаче A (Div.2) проходили решения за O(n) ;( Люди сначала генерируют sqrt(n) треугольных чисел, а потом бегут по ним за квадрат и проверяют сумму. Проходит за 1.9 + eps.
К сожалению, на современных компах 10^9 проходят в две секунды. Это надо начинать иметь ввиду. С другой стороны то, что ты сказал похоже на решение div2A, не так ли?
Почему "к сожалению"-то.
А точно ли за 1.9 с? У меня подобное решение на Java c HashSet ушло 110 мс.
У тебя o(sqrt(n)) как в разборе.
Да, обидно, пытался ламать такое решение на макс. тесте, думал смогу...
Данный текст также введет на "Разбор задач Codeforces Round #122 (Div. 2)".
D решается проще без динамики. Представим себе решение для дерева. Это будет просто половина количества вершин нечетной степени (это можно представить себе так: в каждой вершине нечетной степени обязан быть хотя бы один конец радиальной линии). В кактусе половина количества вершин нечетной степени это минимальное количество радиальных линий. Нужно посчитать, сколько нужно кольцевых. Заметим, что если хотя бы две вершины какого-то цикла имеют степень больше двух, этот цикл "бесплатный": его можно разбить на куски и включить каждый кусок в какую-то радиальную линию. Иначе из цикла нужно сделать кольцевую линию. Итого решение одним обходом в глубину: количество циклов, содержащих меньше двух вершин степени больше двух, плюс количество вершин нечетной степени.
Я в задаче E обошёлся деревом отрезков с единичками и ноликами, нежели Декартовым. Правда, мне пришлось собрать частичные суммы, отсортировать их и написать ещё один бинпоиск.
А я написал декартово, и оно получило TL/15 на претестах. После контеста только досдал ускорением в два раза, вынеся построение дерева из двоичного поиска.
Да, я сам едва-едва влез. 3.9 из 6.0.
"Едва-едва влез" Шлюнкин Леша (sankear) — у него 5.9 из 6, а у тебя — "вальяжной походкой вошел" :-)
В Е зашло еще решение, использующее полный протокол MergeSort для частичных сумм массива. А именно: посчитаем все суммы с 1-го по i-ый элемент, добавим в начало 0. Теперь в бинпоиске надо найти количество пар чисел с разностью >= заданного значения. Запускаемся рекурсивно от половинок отрезка + с помощью двух бегущих по отсортированным половинкам указателей дополняем ответ.
Мое решение C — не видел похожих в обсуждении.
Пусть дерево подвешено. Тогда ответ для ребра — число дураков в поддереве его нижней вершины, пара которых находится не в этом поддереве. Запустим динамику по поддеревьям, которая для каждой вершины будет находить множество таких дураков в ее поддереве. При построении множества для вершины нужно просто объединить множество дураков в ней и множества всех ее детей. При объединении следует выкидывать дураков, которые нашли свою пару. Итак, осталось объединить набор множеств. Применяем стандартный прием (спасибо Nerevar) — при объединении двух множеств вливаем меньшее множество в большее (тогда каждый элемент будет добавлен куда-то не более логарифма раз). Итоговая сложность — O(n*log(n)^2).
Код: 1729330
Клёво. Во всём остальном, что я видел, появлялось lca
Маленькая поправочка к задаче A Модные числа. В первом случае бинпоиск работает не за log N, а за log sqrt(N), т.к. слагаемых у нас примерно sqrt(N). Асимптотика решения выходит O( sqrt(N)*log sqrt(N) ). Спасибо за понимание.
UPD: опередил
UPD2: я опередил
Слово "опередил" само по себе не дает ясного понимания, кто кого опередил, если не видеть историю постов :)
log(sqrt(N)) = log(N) / 2 = O(logN), так что на асимптотику это не влияет.
UPD: опередили
Спасибо, в следующий раз буду иметь это ввиду ( Ведь я ещё не учил логарифмы ). Вы абсолютно правы. Простите за мою поправку.
Таки что считать поддеревом ребра?..
Подвесили за произвольную вершину. Тогда поддерево вершины x — это те, для которых x лежит на пути до корня.
В задаче Е див.1 есть более простое решение, которое не требует декартова дерева. Я использовал тот факт, что при фиксированной правой границе, в качестве левой границы нам подойдет любая точка, что S[r] - S[l] > = x, где х — аргумент бинарного поиска, а S — массив частичных сум. При помощи выше сказанного, можно свести задачу к поиску количества элементов на префиксе, которые не больше какого-то числа.
I wrote code for 191C but I got verdict: wrong answer on test 3. please, tell to me, why my code do not works correctly. link: https://mirror.codeforces.com/contest/191/submission/39604271
English Editorial of 191A — Dynasty Puzzles
We create dp[26][26] where dp[i][j] represents the max. length of a dynasty which starts at letter i and ends at letter j. Since in the question, the first and last letters are to be same, Our answer will be the maximum of dp[i][i] for 0<= i <=26.
Finally , answer will be maximum of all dp[i][i] , where 0<=i<=26.
Code135
Very well explained!
Great Explanation Sir
For anyone looking for a submission for the editorial for C, look at Shik's solution here.
I am finding it difficult to understand the solution of 191C. Can someone please explain how lca is being used here and how it is giving the correct answer? I saw few submissions but didnt understand the idea behind it.