710A - Ходы короля
Легко видеть, что в задаче возможно всего три случая. Если король находится углу доски, то у него 3 возможных хода. Если он стоит на краю доски, то у него 5 возможных хода (если конечно он не в углу). Наконец, если король не стоит на краю доски, то у него всего 8 возожных хода.
Сложность: O(1).
710B - Оптимальная точка на прямой
Легко видеть, что ответ всегд находится в одной из заданных точек (функция суммарного рассояния между парой заданных точек монотонна). Далее можно либо для каждой точки посчитать суммарное расстояние и выбрать оптимальную точку, либо заметить, что ответом является точка находящяяся посередине в отсортированном списке заданных точек (если точек чётное количетсво то слева посередине). Последний факт легко доказыватся, но можно это и не делать и сдать задачу первым способом.
Сложность: O(nlogn).
710C - Магический нечётный квадрат
Задачу предложил Resul Hangeldiyev Resul.
Решение задачи легко получить из второго примера. Легко видеть, что если расставить все нечётные числа в виде ромба посередине квадрата, то мы получим магический квадрат.
Сложность: O(n2).
710D - Две арифметические прогрессии
Эту задачу я уже давно хотел дать на раунд, она мне казалась очень стандартной, но я недооценил её сложность.
Запишем уравнение, которое описывает все решения задачи: a1k + b1 = a2l + b2 → a1k - a2l = b2 - b1. Имеем линейное диофантово уравнение с двумя неизвестными: Ax + By = C, A = a1, B = - a2, C = b2 - b1. Его решение имеет вид: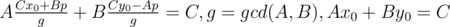 
, где последнее уравнение решается с помощью расширенного алгоритма Евклида, а p произвольное целое число. Далее нам нужно удовлетворить двум условиям: 
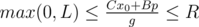и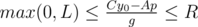 
. Поскольку мы знаем знаки чисел A и B, последние уравнения задают отрезок возможных значений для переменной p, длина этого отрезка и является ответом на задачу.
Сложность: O(log(max(a1, a2))).
710E - Генерация строки
Задачу предложил Zi Song Yeoh zscoder.
У этой задачи есть простое решение, которое участники описали в комментариях. Моё решение несколько сложнее. Будем решать задачу с помощью динамического программирования. zn — наименьшее время, необходимое для получения n букв 'a'. Теперь рассмотрим переходы: переходы на дописывание одной буквы 'a' будем обрабатывать как обычно. Переходы на умножения на два и вычитание единицы будем обрабатыват одновременно: будем считать, что сразу после умножения числа i на двойку мы сразу сделаем i вычитаний и далее будем проталкивать от нашего числа вперёд такие обновления. Легко видеть, что такие обновления никогда не никогда не вкладываются, поэтому их можно хранить в очереди, дописывая очередное обновление в конец очереди, и, забирая лучшее обновление с начала очереди. Решение достаточно сложное на объяснение, но очень короткое, поэтому лучше посмотреть код :-)
Сложность: O(n).
710F - Операции над множеством строк
Задачу предложил Александр Кульков adamant.
Сначала научимся избавляться от запросов на удаление. В силу условия, что никакая строка не добавляется дважды (и, соответственно, не удаляется) нам достаточно посчитать ответ для всех добавленных строк (как будто они не удалялись) и вычесть из него ответ для уже удалённых. Таким образом, можно считать, что строки только добавляются.
Далее воспользуемся алгоритмом Ахо-Корасик. Единственная проблема, заключается в том, что алгоритм строит правильные суффиксные ссылки только после того как все строки добавлены. Чтобы решить эту проблему заметим, что ответ для набора строк равен ответу для некоторой части этого набора плюс ответ для оставшейся части. Далее воспользуемся стандартным приёмом превращения статической структуры данных (Ахо-Корасик в данном случае) в динамическую.
Пусть в данный момент в набор добавлено n строк, тогда мы будем хранить не более logn наборов строк размера разных степеней двойки. Добавим строку в набор размера нулевой степени двойки и далее перебрасывать наборы к большим степеням двойки, пока не получим инвариантный набор множеств.
Легко видеть, что каждая строка перебросится не более logm раз и на каждый запрос мы умеем отвечать за O(logm).
Сложность: O((slen + m)logm), где slen — суммарная длина всех строк во входном файле.
Добавь, пожалуйста, ссылку на разбор в анонс и в материалы соревнования.
Done.
In problem B , How do we prove that "the answer is always in one of the given points" .
Sort the array, and just find the median.
Why we can forget about them ?
Because, they're part in the answer is length of the interval, and we can just add this interval in final sum, and then forget
I just want to detail TaTaPiH's answer a bit more, but he has 100% of the credits (thanks btw).
Let the two points be x1 and x2. If you take a point y between x1 and x2 (x1 <= y <= x2) the sum of distances to get to y is (y — x1) + (x2 — y) = x2 — x1, which means that independent of the point y you take, the total distance will be the same (the length of the segment).
Let's sort array x which has the n points, 1-indexed. For example, suppose n = 5. We want to minimize the total sum of distance to some selected point y.
Consider points x[1] and x[5]. These 2 points alone will always sum (x[5] — x[1]) to the final sum of distances if you choose some (any) point y between them. (See case n = 2 for explanations). So let's sum that to the final sum and move on.
Now we're left with points x[2], x[3], x[4]. For points x[2] and x[4] you should also take a point y between them, because otherwise a point y outside points x[2] and x[4] would sum something greater then the length of that interval to the final answer. Note that a point between x[2] and x[4] is a point between x[1] and x[5] so you can continue this logic without changing the answer for the previous points. Now only one point (x[3]) is left, see case n = 1.
So the pattern is: you fix 2 extremes points (one to the left and one to the right), now you'll now that an optimal answer must choose a y between them, and move on to the next points, until you're left with 1 or no points.
Assume that we are moving a point from left to right to get the optimal answer, consider the following scenario. (X denotes a point, # denotes the current chosen point)
(XXX m points XXX) # (XXX n points XXX)
Whenever you move to the right, the resulted total distance changes by n-m since you are moving closer to n points and moving away from m points. At one point, when n becomes smaller equal than m, you need not to continue go right for the answer since we only need the leftmost point as the answer. Hence, the answer is always one of the given points.
Where is english version?!
Google translate
Does'nt seem to be working well
English version please? :(
Хочу рассказать о более простом, не связанном с математикой, решении в задаче Д. Не сложно догадаться, что общие числа (если такие есть) в двух арифметических прогрессиях так же являются арифметической прогрессией с шагом
a = a1 * a2 / gcd(a1, a2)(единственная математика в этом решении). Рассмотрим два случая.Первый случай, если
a > 10^6. В этом случае количество чисел попавших в отрезок[L, R]будет не велико, и один из шагов (a1илиa2) будет достаточно большим. Более точно — в худшем случае минимальное значение наибольшего шага равно10^3. В таком случае можно просто идти по элементам прогрессии с наибольшим шагом и проверять: 1) принадлежат ли эти элементы второй прогрессии, 2) лежат ли они на отрезке[L, R].O( ( R - L ) / max( a1, a2 ) ).Второй случай, если
a <= 10^6. В этом случае наименьший из шагов примет небольшое значение. Более точно — в худшем случае он может быть равен10^6(например, еслиa1 = a2 = 10^6). Не трудно догадаться, что для того, чтобы в первой прогрессии найти элемент принадлежащий второй прогрессии, надо сделать не болееa2шагов, аналогично и для второй — не болееa1шагов. Соответственно надо выбрать ту прогрессию, где шаг больше, а количество шагов меньше. Если после того как мы сделали эти шаги, мы так и не пришли в общий элемент, то прогрессии не пересекаются и ответ0. В противном случае мы пришли в общий элементb. Остаётся убедиться, что он удовлетворяет условиямb >= b1 && b >= b2. Если нет, то можно его легко сделать таковым, используя шагa(например,k = ( b2 - b + a - 1 ) / a; b += a * k;). Теперь, когда мы свели две прогрессии к одной, задача становится совсем простой. Её можно решить, например, бинарным поиском отдельно дляRи отдельно дляL - 1.O( min( a1, a2 ) + log( R ) + log( L ) ).Решение
Также можно объединить эти две идеи в одно решение. То есть, либо мы достаточно быстро придём в общий элемент (если
min( a1, a2 )небольшое), либо достаточно быстро покинем отрезок[L, R](еслиmax( a1, a2 )большое).P.S. Во время виртуального участия я писал совсем другое решение, в котором так же искал первый элемент новой прогрессии, только более эвристическим способом.
P.S.S. Парадоксальная ситуация. В одном случае я называю
10^3достаточно большим число, а в другом10^6— небольшим числом."Не трудно догадаться, что для того, чтобы в первой прогрессии найти элемент принадлежащий второй прогрессии, надо сделать не более a2 шагов, аналогично и для второй — не более a1 шагов."
По-моему до этого довольно трудно догадаться. Не подскажете, как это доказать?
Рассмотрим случай, когда мы движемся по первой прогрессии. Проверка того, принадлежит ли элемент второй прогрессии заключается в том, что разница между первым элементом второй прогрессии и рассматриваемым элементом первой прогрессии должна быть кратна шагу второй прогрессии (более коротко:
abs( bb1 - b2 ) % a2 == 0, гдеbb1 = b1 + k * a1,k— какое-то неотрицательное число. Разумеется также должно выполнятьсяbb1 >= b2, но этого лучше достичь после нахождения общего элемента). Допустим, изначально остаток от деления равенb1 % a2 = c. Послеa2шагов мы сместимся наa1 * a2, а значит остаток от деления вновь будет равенc(( b1 + a1 * a2 ) % a2 = b1 % a2 = c). Делая дальнейшие шаги, мы опять будем попадать в те же остатки, что и до этого. Соответственно, если заa2шагов мы не попали в нулевой остаток, то мы никогда в него не попадём.Большое спасибо!
This round is important and must have an English Editorial.
Codeforces is a good international site.
Please don't limit us by only releasing in Russian. I kindly request you to release an English version.
A lot of people are making a great effort to learn english to understand and take place in the community. Are U serious with this EDITORIAL in russian? I hope an english version release of this editorial.
In particular I am very interested in the solution for problem F.
Sorry for the delay with English editorial. I'll write it as soon as I can.
TNX ;))
Now,Thanks!
Дорешал F, и что могу сказать — хэши затащили. Правда работали 2963 мс, что почти Time Limit. Написал вот что: структура
map[длина строки][хэш] = количество, а так же использовал set для хранения всех имеющихся в текущий момент длин строк. Понятно, что запросы 1 и 2 типа будут обрабатывать за длину строк на логарифм. Что же касается запросов 3-о типа, вот какой я нашел самый плохой случай: допустим у нас есть строки всех длин от 1 до 500 (суммарная длина таких строк чуть больше10^5). Исходя из этого к нам может поступить запрос третьего типа со строкой длиной2*10^5. Обрабатываться он будет соответственно около10^8операций, плюс два логарифма от set и map (хотя логарифм от map вырождается в O(1) ввиду того, что имеется всего одна строка каждой длины). Исходя из такого расчета, моему решению очень повезло уложиться в 3 секунды, либо просто в тестах не был рассмотрен данный случай.Решение
UPD: Решение с одиночным хэшем отработало за 1.5 с.
UPD2: Таки нет, в тестах (тесты 21 и 22) есть нечто похожее на описанный здесь случай.
Очень понравилось авторское решение задачи F. Особенно два момента: заменить операцию удаления операцией добавления в другую структуру, и сделать разделение структуры на логарифм структур. Спасибо за задачу.
Longing For Solution in English...
Can someone please explain to me the logic behind problem E. I have used a 1-D array to store the least time to generate i no. of a's.
Let dp[i] be the optimal cost to produce string of length i. We have two cases:
If i is even, then the optimal cost for dp[i] is the minimum of dp[i-1] + x (add new char) or dp[i/2] + y (copy from half the length)
If i is odd, then the optimal cost for dp[i] is the minimum of dp[i-1] + x (add new char) or dp[(i+1)/2] + x + y (copy then remove). For example, you can get string of length 15 either by adding from length 14, or copy from length 8 then removing 1 character
(Note: I don't know if this is the logic used in the editorial code)
I have previously implemented the same.But it is showing incorrect. This approach fails in the following case.
Suppose we want to produce the string of length 30 then according to above approach dp[15]=min(dp[8]+x+y,dp[14]+x)
dp[30]=min(dp[15]+y,dp[29]+x)
you can see that we are having an extra x seconds(which is the same time spent in removing an extra 'a' generated from doubling 8 a's) while calculating dp[30]. Now if we want to produce a string of higher length then there would be more and more extra x seconds while calculating the cost.Hence this approach won't work.
First of all, how do you know that dp[15] must be dp[8] + x + y? It could also be dp[14] + x, depending on the x y values.
Secondly, I don't quite get what you mean by "more and more extra x seconds", but looking at your submissions, I guess your mistake is implementing the dp when i is odd as min(x + v[i/2] + y, v[i-1] + x). It should be v[(i+1)/2]
I don't get something
Lets say i is even, then you that dp[i] is the minimum of dp[i-1] + x or dp[i/2] + y, but why can't it be dp[i+1]+x, like if we can get to 31 faster then to 29, and we need to get to 30. Same question if i is odd.
EDIT: Nvm figured it out
Can you please explain why we aren't considering dp[i+1]+x, I am having the same doubt?
for those still having this doubt..
consider the case when i is even say 30..then one possible choice for making 30 is cost(30)=cost(15)+y which is considered in the above recursion...but another possible choice can be cost(30)=cost(16)+2*x+y when cost(16) is lesser than cost(15)..in this case cost(15) maximum value can be cost(16)+x..so replacing the maximum value of cost(15) in the equation cost(30)=cost(15)+y it becomes->cost(30)=cost(16)+x+y which is still lesser than cost(16)+2*x+y...so when i is even we can say that its optimal answer will be among cost(i-1)+x and cost(i/2)+y only..
we can similarly prove it for the odd case..
can u please explain dp recurrence a little?
I solved problem 710E - Generate a String using Dijkstra, but it got AC with 1918ms :D almost TLE
could anyone explain the other solution using Dynamic programming?! i did not understand what is written in the editorials!!!
Hi, my interpretation of the solution was that instead of using Dijkstra, they managed to use a slightly-different graph that was a DAG, so finding shortest paths is O(N).
You can note that between doubling operations (after the first one, of course), there is at most one + or — operation, because otherwise you could be more efficient by moving them before the previous doubling operation. (for example, the sequence +*++ -> 4 could be done as ++*). If you take a graph with only these edges, it becomes a DAG, and dijkstra is not necessary.
EDIT: Here is incredibly simple solution with this idea http://mirror.codeforces.com/contest/710/submission/20469970
Amazing idea!!
Incredible!!
But it seems more acurate to say there is at most one
+or-after*, because*++can be replaced with+*and*--can be replaced with-*. With this statement we know if there exists*in the path, the end of the path is one of*+,*-and*.If you say "there is at most one
+or-between two*, there can be more than one+or-after the last*", it contradicts the above statement.Can I see your code please? my code works with Dijkstra but I got TLE I wanna see if I can do any thing about it!
Did anyone solve problem D?
I know how to derive x0, y0, where Ax0 + By0 = C by using Extended Euclidean Algorithm, but I don't know proceed from here to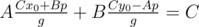
. Also, it seems to me that 
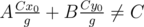. Am I misunderstanding something? If not, can somebody perhaps elaborate more on this step? Thank you!
Also obviously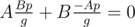
, so the first equation is also true.
The only difficulty thing is to prove that all solutions can be described in the given form. It is a standard fact and I think you can easily find the prove in the internet.
I found that no one can solve Problem F by Java 8 because of TLE in test case #19 (demands flush*300000) though problem statement refers to Java's flush.
Did writers&testers check whether it can be solved by Java 8?
What is the "floor (y0*C, A)" in the end of problem D's code for? Why is it here ? How did we get to "y0*C/A" ?
Proof of Problem E , DP — Solution
Hello can someone explain why I got a TLE on test B?
Here is the code: https://mirror.codeforces.com/contest/710/submission/91295249.
I believe it is because I use Java but I am not sure. Is that correct?
In ques D, I first calculated solution of x0,y0 using extended Euclid algo, and then i found the value of x=a1*x0+b1, and from their i found the req. resutlt as possible solutions will lie at a jump of lcm(a1,b1) from x. BUT, while calculating x, x is getting overflow because of large value of x0 and a1, in test case 78, can anyone tell me how to solve it. Thanks
I have a (logn)^2 approach to solve problem, could be reduced to O(logn) if map is not used.
I have a assertion that,
let j=log2(i); the best way to reach i is,
1). either reach j and then use operation 1 (x) to reach i.
2). either reach j+1 and then use operation 1 (x) to reach i.
3). if i is even then reach (i/2) and use operation 2 (y) to reach i and if i is odd then reach (i/2 and do operation 1 and operation 2 to reach i) or reach (i/2+1 and do operation 1 and operation 2 to reach i ).
These are the possible best transitions, and we easily calculate best way to reach i if i is power of 2.
My submission:- https://mirror.codeforces.com/contest/710/submission/93869685
Problem F — String Set Queries can be solved using hashing. It seems easier to me than Aho-Corasik solution.
Wow, I actually managed to solve a 2400 problem without looking at the solution! >.<
I have a different solution than the editorial. There's no need for Aho Corasick, finite-state machines, tries, or anything like that. It's just suffix array and hashing.
So once we construct our suffix array, we can effectively partition things into "blocks". So like say we have the string "caccc"; then the suffix array will correspond to:
accc
caccc
c
cc
cc
At the first iteration, we have several "chunks" of blocks which are the same
accc
caccc
c
cc
cc
At the second iteration, once we look at prefixes of suffixes of length two, we have some more chunks:
accc
caccc
c
cc
cc
And so forth. Effectively, at the $$$i$$$th iteration, all chunks correspond to suffixes whose prefixes of length $$$i$$$ are the same. It's easy to update these chunks: offline, check the least common prefix between pairs of consecutive entries in our suffix array and make a new chunk divider at that point. If we use some dynamic data structure, like a set, to keep track of chunks, the complexity of this chunk-finding is $$$O(|S| \log (|S|)$$$.
For each chunk, we want to know if it's corresponding prefix of length $$$i$$$ is in the array. That will be $$$O(|S| \log (|S| \cdot \sum {\text{# of chunks at ith iteration}})$$$. That's pretty bad because we could have a lot of chunks.
But actually, a lot of chunks are useless. If a chunk does not correspond to a prefix of anything in $$$D$$$, we can ignore it.
But how do we know if a chunk corresponds to a prefix in $$$D$$$? I used hashing. So I hashed all the prefixes of elements in $$$D$$$ using a rolling hash. Then I put all those hashes into a map. Then, I rolling hash the corresponding prefix-suffix chunk thing in $$$S$$$. And check if it's in the map.
To find the answer, at each iteration, check if a chunk corresponds to something in $$$D$$$ (again can be done using hashing).
Code is kind of long (265 lines long). Most of the code comes from generating the suffix array and hashing (I used 3 hashing moduli to ensure no collisions). So it's actually not as long as it seems.
The end.