Задача: даны два множества точек на плоскости (оба размером N), нужно найти совершенное паросочетание с минимальным весом самого тяжелого ребра в нем (вес ребра — очевидно, Евклидово расстояние). Я умею решать Куном с бинпоиском по весу самого тяжелого ребра за O(N3 logN). Вопрос: как решить эту задачу за чистый куб путем добавления в алгоритм какой-то жадности? Хопкрофта-Карпа и Диница прошу не предлагать. Ответ: вот так.
Задача о поиске совершенного паросочетания в регулярном двудольном графе объяснялась в харьковской ЗКШ в этом году, но только для тех графов, в которых степени каждой вершины являются степенями двойки. Вопрос: как решать эту задачу для графов с произвольными степенями вершин? Применение алгоритма Хопкрофта-Карпа очевидно, но мне кажется, что существует что-то побыстрее.
Задача: дан регулярный граф, нужно найти в нем гамильтонов цикл. Вопрос: существует ли алгоритм, который гарантированно найдет этот гамильтонов цикл за полиномиальное время, если он имеется?
Эта задача с Тимуса имеет очевидное решение через паросочетание. Вопрос: можно ли обойтись без паросочетания и решить задачу жадно? Ответ: да, можно, а я тупой идиот, потому что думал как раз о таком решении, но не удосужился проверить 3 случая.
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 17:42:50 (h2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










2) Можно искать быстро (за O(m)), но это не совсем просто. Я знаю только алгоритм, который начинает с дробного паросочетания и постепенно округляет его до целого; хотя возможно есть что-то и попроще, по этой теме гуглится много разнообразных статей.
3) Нет^W Такого алгоритма науке неизвестно, доказано, что эта задача NP-complete.
3) И что отсюда следует?))
Из этого следует, что, если полиномиальный алгоритм найдётся,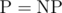
О чём и речь, копетан) Полиномиальный алгоритм вполне себе может существовать.
3) а в двудольном ищется за полином? помню, например, макс. клика ищется, интересно про другие NP.
Ну я про это ничего не знал, но в википедии написано, что эта задача NP-complete даже для bridgeless undirected planar 3-regular bipartite graphs.
Я вчера ночью нагуглил, что в k-регулярных планарных графах с k >= 6 гамильтонов цикл ищется за полиномиальное время, но сам алгоритм не нашел (потому что почти не искал).
О, у меня тоже есть один вопрос про паросочетания, с этими не связанный: есть задача про покрытие ориентированного ациклического графа минимальным количеством неперескающихся путей, её решение описано на е-максе. Допустим, что пути могут пересекаться, тогда достаточно просто транзитивно замкнуть исходный граф и воспользоваться предыдущим решением. Проблема в том, что решение первой задачи работает за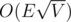 , а второй уже за O(V2.5). Вопрос — можно ли как-то использовать особый вид получившегося графа и ускорить решение?
, а второй уже за O(V2.5). Вопрос — можно ли как-то использовать особый вид получившегося графа и ускорить решение?
Ну так транзитивное замыкание все равно за куб ищется. После этого можно паросочетание уже как угодно находить.
И впрямь. Тогда интересно, как решать эту задачу(если не хотите регаться, то там 70 тестов, V ≤ 1000, E ≤ 10000, TL 4 секунды).
Транзитивное замыкание ищется за O(VE) запуском обхода из каждой вершины.
Но даже если искать его за куб, то это очень быстрый куб из-за битовых операций.
4) каждый квадрат 4 на 4 обрабатываем отдельно — кладем либо два кирпича горизонтально либо вертикально
наверное, каждый квадрат 2 на 2 (или я не понял идею)?
действительно 2x2 имелось ввиду
4) да, простое решение: сначала во втором слое выложим все плитки вертикально. Допустим, какая-то из плиток совпала со своей нижней. Тогда берем эту плитку и соседнюю с ней(соседняя имеется в виду та, у которой граница проходит по двум клеткам). Перекладываем их горизонтально. После этого совпадений нет.
1) Можно попробовать применить min-cost-max-flow. Паросочетание минимальной стоимости за куб мы находить умеем, если использовать дейкстру с потенциалами. Искать дейкстрой путь, в котором максимальное ребро минимально, мы тоже умеем, но здесь уже не получится так халявно добавить потенциалы (у сложения есть обратная операция, а у взятия обратного — нет). Если мы научимся добавлять потенциалы/каким-то другим способом искать кратчайший путь за O(V2), то будет решение ра куб.
Собственно, соображение, по которому не должна работать никакая жадность: если бы жадность работала, то паросочетания минимального веса можно было бы искать почти такой же жадностью.
upd: А не правда, что построив паросочетание минимального суммарного веса, мы в случае евклидовой плоскости решим и исходную задачу?
Контрпример чуть ниже.
А как все-таки находить паросочетание минимальной стоимости за куб?
UPD. Или Вам нужно рассказать Дейкстру с потенциалами поподробнее?
Нет, спасибо, думал, может какой-то метод есть интересный еще — как-то не вспомнил, что это и есть по сути венгерский алгоритм.
̶1̶)̶ ̶В̶е̶н̶г̶е̶р̶с̶к̶и̶й̶ ̶а̶л̶г̶о̶р̶и̶т̶м̶ ̶р̶е̶ш̶и̶т̶ ̶э̶т̶у̶ ̶з̶а̶д̶а̶ч̶у̶ ̶з̶а̶ ̶к̶у̶б̶.̶ ̶Н̶а̶ ̶е̶м̶а̶к̶с̶е̶ ̶е̶с̶т̶ь̶ ̶ч̶т̶о̶ ̶п̶о̶ч̶и̶т̶а̶т̶ь̶ ̶п̶о̶ ̶э̶т̶о̶й̶ ̶т̶е̶м̶е̶.̶ В следующий раз обещаю внимательней читать условие...
Контрпример на сведение к задаче о назначениях: N == 2, первое множество: (0, -2) и (0, -1), второе множество: (0, 1) и (0, 2).
После сборов везде венгерка мерещится? =)
есть немного
1) Если паросочетание искать не Куном, а Диницем или алгоритмом Хопкрофта-Карпа, сложность будет O(N^(5/2)*log(N))
Это решение очевидно, надо было про него написать в топике. Меня интересует алгоритм не сложнее Куна (а, может быть, де-факто им и являющийся).
---придумал пример на котором не работает---
1) Подробностей не помню, но я точно писал какое то такое решение за точный куб: сортим все ребра по длине и запускаем куна. Как только не можем насытить вершину, то добавляем ребер до тех пор, пока не получится насытить. Если вспомню подробности — допишу.
upd. даже вот нашел задачу в архивах: http://acm.sgu.ru/problem.php?contest=0&problem=218
upd2. Ну вроде все. Когда насыщаем вершину, мы там строим дерево обхода бфс или дфс чтобы найти чередующуюся цепочку. Помечаем вершины обхода. Если не насытили — пробуем добавлять ребер, пока не добавим ребро из помеченой в непомеченную, запускаем дополнительный бфс/дфс по этому ребру (и опять же отмечаем вершины где побывали). И так далее. На одну насыщаемую вершину, в итоге получим чистый квадрат (потому что по сути у нас запуск одного бфс/дфс в несколько приемов). На весь алгоритм — чистый куб.
Большое спасибо за объяснение. Как раз то, что надо. Завтра на свежую голову реализую.
когда/если реализуете пожалуйста выложите сюда код, а то обяснение я понял не на 100%, а с кодом будет полностью понятно.
Как с паросочетаниями решать?
В-общем, нужно построить вот такой граф и найти в нем паросочетание (клетки раскрасил для наглядной демонстрации его двудольности).
