Tudor's blog

Count the spanning trees in a grid graph
By Tudor, history, 8 years ago, In English

Hi , I am interested to solve a problem and I can not find a polynomial solution . How many spanning trees are in a grid graph(N x M)?

  • Vote: I like it
  • +18
  • Vote: I do not like it

Comments Comments (6)
| Write comment?
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

If you're looking for an O((mn)O(1)) solution take a look at this.

Perhaps because of the special characteristics of the graph the determinant can be computed faster?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you explain the whole solution , please?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it +21 Vote: I do not like it

      The answer for you question is the value of the determinant of the graph's Laplacian matrix. This matrix is computed multiplying the adjacency matrix by -1 and then adding the degree of each node on the main diagonal. Forgot to mention, after this you will have to erase the line and the column of an arbitrary vertex. You can consult this paper for proof. This will lead to a O((N * M)3) solution using Gaussian Elimination. I belive LU decomposition will work better on this kind of matrix though.

      An easier particular case is when M = N.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        This is the easier case? I can't even tell if this is an integer...

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
          ← Rev. 3   Vote: I like it +13 Vote: I do not like it

          Let F be a field with an element ω of order n i.e. ωn = 1. Then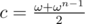 is like 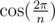. From 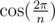, we can get 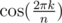for any integer k using Chebyshev polynomials. If the base field has no such ω, we can extend this field to F[X] / (Xn - 1). Edit: X^n-1 probably doesn't work. Just generate some irreducible polynomial.

          I think, using that, we can solve the problem (taking word-size prime mod) in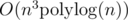 time. There is a similar formula for n ≠ m case which can be used to get similar time bound. I haven't implement any of these so I'm not sure if this really works.

          → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

You can use the Kirchhoff Theorem! It has the same complexity as computing the determinant of a matrix (which is polynomial, using Gaussian Elimination).

This Spoj problem is exactly what you describe :) Maze

→ Reply