Полное видео скачается через all = (c·a + b - 1) / b секунд. В этой задаче можно было перебрать величину ответа 1 < = t < = all. Чтобы удовлетворить условию задачи, достаточно проверить, что в последний момент времени t0 = all выполняется условие, написанное в тексте задачи, а именно t0·b > = (t0 - t)·a.
В этой задаче нужно было аккуратно реализовать описанный в условии процесс. Вначале заметим, что мяч с номером i > m попадет в одну корзину с мячом под номером i - m. Поэтому достаточно распределить первые m мячей. Это удобно сделать при помощи двух указателей lf, rg, начиная с середины. Поочередно кладем мяч сначала слева, затем справа и двигаем указатели. Единственный раз, когда нужно дважды подвинуть левый указателей, возникает в самый первый момент, если m нечетно.
Данная задача носила реализационный характер. В своем решении я поступал следующим образом. Удалим из текста все пробелы, кроме пробелов в сообщениях try-catch блоков. Затем при появлении слова try, кладем номер нового try-catch блока в стек. При появлени слова throw, запомним его тип, а также текущее состояние стека (то есть какие try-catch блоки открыты). Для этого, например, положим номера открытых блоков в set. При появлении слова catch, если тип блока совпадает с типом оператора throw, а также номер текущего блока находился в стеке при появлении оператора throw (то есть он есть в нашем set-е), то сразу выводим ответ. Иначе удаляем текущий try-catch блок из стека. Если подходящего try-catch блока так и не найдется, в конце выводим фразу "Unhandled Exception".
Разбор от автора Igor_Kudryashov
В данной задаче были заданы по сути прямые в виде yi = ki * x + bi, но в тех точках, где y принимает отрицательное значение, оно заменено нулем. Необходимо было найти количество углов, не равных 180 градусам, в графике функции, равной сумме функций указанного вида.
Во-первых, несложно показать, что сумма прямых является прямой. В самом деле, если y = y1 + y2, то y = k1 * x + b1 + k2 * x + b2 = (k1 + k2) * x + (b1 + b2). Рассмотрим точки, в которых yi = 0, т.е. xi = - bi / ki. Пока предположим, что ki не равно 0. Тогда i-ая функция разбивается на две прямые, одна из которых тождественно равна 0. Оставим среди xi различные точки и упорядочим их по возрастанию значения. Тогда, очевидно, между двумя соседними точками суммой заданных функций является прямая. Найдем уравнение этой прямой. Предположим, мы рассматриваем i-ую слева точку. Тогда если уравнение прямой между i-ой и (i + 1)-ой точками, отлично от уравнения прямой между (i - 1)-ой и i-ой точками, тогда в i-ой точке образуется угол, не равный 180 градусам.
Таким образом, нам необходимо найти уравнение прямых на отрезках между соседними точками x, т.е. найти коэффициенты k и b. Это можно легко сделать с использованием 2 массивов запросами увеличения на отрезке в оффлайне.
Когда мы обрабатываем очередную функцию, мы смотрим, если ki равно 0, то нужно ко всем отрезкам прибавить одну и ту же величину, но т.к. данное изменение не повлияет на ответ, то можно не обрабатывать функции такого вида. Если ki не равно 0, то найдем индекс j точки xi в упорядоченном списке x. Теперь если ki больше 0, то нужно сделать увеличение на суффиксе, начиная с позиции j, иначе нужно сделать увеличение на префиксе до позиции j (при этом увеличение на префиксе коэффициента k будет производиться на отрицательную величину).
Разбор от автора Fefer_Ivan
В этой задаче самой долгой операцией является поиск корня вершины и длина пути до него. Эту операцию можно выполнять быстро используя эвристику сжатия путей. Такой же метод применяется в структуре данных Disjoint Set Union.
Для каждой вершины v мы будем хранить два числа: c[v] и sum[v]. c[v] = v, если v — корень, иначе c[v] — следующая вершина на пути от v к корню. sum[v] = сумме длин ребер на пути от v до c[v].
Таким образом для того, чтобы добавить ребро из u в v веса w, достаточно c[u] = v, а sum[u] = w. Теперь мы можем за O(n) находить по вершине нужные нам в задаче root(v) и depth(v) просто переходя каждый раз из v в c[v] и суммируя все sum[v] по пути.
Заметим, что мы только добавляем ребра, но не удаляем. Это значит, что если мы для вершины v нашли root(v) и depth(v), то можно присвоить c[v] = root(v), sum[v] = depth(v). Таким образом в следующий раз мы найдем предка вершины v за О(1). В общем реализация этого подхода выглядит следующим образом:
int root(int v){
if(c[v] == v){
return v;
}else{
int u = root(c[v]);
sum[v] = (sum[c[v]] + sum[v]) % M;
c[v] = u;
return u;
}
}
Доказывается, что такая реализация работает в сумме за время, пропроциональное обратной фунции Аккермана http://en.wikipedia.org/wiki/Ackermann_function#Inverse) на запрос при применении ранговой эвристики. Поскольку в этом случае нельзя её применить, то такой запрос обрабатывается за log(n). Итого получаем решение за время O(n * log * (n)).











Альтернативное решение по B: Заметим, что у нас в задаче определен оператор сравнения чисел от 1 до m. Положим их все в вектор
aи отсортуруем по этому оператору.А дальше просто:
Ошибся, спасибо. Отличное решение Вань)
В C еще можно было идти по блокам в обратном порядке, если команда catch — добавим в стек, если try — достанем из стека соответствующий catch, если throw — ответ — первый в стеке подходящий catch или Unhandled exception, если такого не нашлось.
Что-то у меня сильно проще решение по D. В массив записываем все числа вида -(b / k), где k != 0, сортируем, ищем количество разных чисел.
На самом деле в D достаточно найти количество различных точек в которых прямые пересекают ось ОХ.
я так и делаю, но у меня ошибка на 52м тесте. не подскажете, в чем проблема? код:
int main() { int n; cin >> n; set points; long long k, b; for (int i = 0; i < n; ++i) { cin >> k >> b; if (k == 0) { continue; } points.insert((-b + .0) / k); } cout << points.size() << endl; }
мб, ошибка сравнения чисел с плавающей точкой?
set какой? float? тогда дело в этом наверное. деление для плавающей точки не такое уж и точное, видимо где-то не совпало.
сет double, но ответ сильно отличаеться, от нужного
Вывод 21 Ответ 111
Если заменить double на long double и соответственно послать под gcc то такое заходит.
Я на всякий случай сравнивал не даблы а сделал сет пар, где пара — несократимая дробь
в D можно попроще
пусть уже есть некоторая ломанная, что будет кода добавляем новую ломанную из двух звеньев? В местах где у нее есть производная новых изломов не появится а старые не пропадут. Действительно, если излома не было то получаем сумму двух функций, у которых в этой точке производная есть, у самой суммы тоже будет. Пусть был излом и исчез. Тогда у суммы есть производная в этой точки, у того что мы добавляли — тоже есть, значит и у того что было должна была быть — противор.
В точке излома по аналогичным рассуждениям добавляется новый излом, если его там не было, а если был то остается. Почему остается? хмм.. Во время контеста я об этом не думал) Но на самом деле действительно остается, можно по индукции показать что все изломы направлены углом вниз, если изломы совпадают при добавлении, угол становится острее.
Тоесть, нужно просто посчитать количество несовпадающих изломов добавленных двухзвенных ломанных. Координата излома = -b/k, очень быстро программа пишется на ruby с использованием класса для рац. дробей.
Ахах, все уже отписались. Ну пусть будет поподробнее)
Здесь, наскольно я понял, в задаче E описана только эвристика сжатия пути в DSU, но без обьединения по рангу. Разве такая реализация работает за время пропроциональное обратной фунции Аккермана или все-же за логарифм, как было доказано тут?
UPD. Или все-таки я что-то неправильно понял?
http://en.wikipedia.org/wiki/Disjoint-set_data_structure#History
А я ошибаюсь, или там доказывалась асимптотика при использовании двух эвристик вместе?
В этой задаче нельзя делать объединения по рангу, так что на самом деле решение работает за логарифм.
По C можно гораздо проще, без стеков и сетов, просто с одним счетчиком (т.к. программа гарантированно правильная).
Все, что до throw, можно игнорировать, потом считать количество встреченных try (чтобы пропустить такое же количество catch). Вывести первый непропущенный catch с совпадающим типом исключения, или Unhandled Exception.
См., например, 1779055 или 1778103.
A в одну строку: cout << ceil((a*c-b*c)/b);
В этой задаче такое заходило, но в общем случае безопаснее делать округление частного вверх целочисленно: ceil(a/b) = (a+b-1) div b.
По задаче B можно предложить еще одно решение. Для каждого i-го мяча (1 <= i <= n) делать следующее: если числа (i — 1) mod m и m разной четности, то i-ый мяч класть в корзину с номером (m + (i — 1) mod m + 1) div 2; иначе i-ый мяч класть в корзину с номером (m — (i — 1) mod m) div 2.
http://mirror.codeforces.com/contest/195/submission/1784693 можете посмотреть почему TL? ведь сортирую бысро
В сортировке у вас написано x = a[l + random(l+r-1)]. Но l+random(l+r-1) может получится больше r, т.е элемент разделитель получится больше любого числа из интервала a[l..r], поэтому такой разделитель неудачный. Неудачных разделителей у вас получится довольно много и сортировка будет работать за O(n^2).
random(r+l-1) получает больше r, и мы уже не в отрезке [l,r], а значит она вообще не правильная. я только удивляюсь, как она вообще дошла до 10 теста, и раньше не упала!!!
Често говоря, это новый вид сортировки. Ты сортируешь не правильно. Потом eps надо уменьшить, и ты не рассматривал случий когда ответ 0!!!!
Вот 1785948 исправил!!!
Про eps спасибо sdryapko !
eps надо уменьшить :)...0.0000000000000000001<0.000000001 :)
откуда берется эта константа?
просто привел пример, что человек немного неправильно выразился. А вообще, ИМХО, эту задачу стоило решать в целых числах.
Откуда берется эта константа не представляю, мне лень считать количество 0.
Оценим разность велечин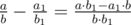 . Можно добиться, чтобы числитель был 1, а знаменатель незначительно меньше 1018.
. Можно добиться, чтобы числитель был 1, а знаменатель незначительно меньше 1018.