Если первый игрок своим ходом не может поставить тарелку на стол (стол слишком маленький, и тарелка не помещается, т.е. 2r > min(a, b)), выигрывает второй игрок.
Иначе выигрывает первый игрок. Выигрышная стратегия такова: первый игрок ставит свою первую тарелку в центр стола, а затем симметрично отражает ходы соперника относительно центра стола стола. Легко видеть, что если в этом случае второму игроку удастся совершить ход, первому это также удастся. А если не удастся, первый игрок победит, что ему и было нужно.
Решение задачи — разбор случаев.
Легко понять, что важны лишь степени многочленов и их коэффициенты при старшем члене, остальные числа в инпуте — для отвода глаз.
- Если степень знаменателя больше, ответ равен "0/1".
- Если степень числителя больше, ответ — бесконечность. Чтобы понять, какая именно, надо посмотреть на знаки при старших коэффициентах. Если знаки одинаковые, то положительная, иначе — отрицательная.
- Если степени числителя и знаменателя равны, ответ, как известно из курса математики, равен
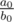. Чтобы дробь была несократимой, надо a0 и b0 поделить на их gcd. Также надо быть внимательным, если один или оба из этих чисел отрицательные и не вывести "1/-2" вместо "-1/2".
196A - Лексикографически максимальная подпоследовательность
Очевидно, что сначала нам надо выписать все буквы 'z', если они есть — ответ от этого хуже точно не станет. Теперь множество доступных букв сократилось — мы не можем использовать те буквы, что находятся левее последней буквы 'z'. Поэтому выпишем все буквы 'y', что встречаются правее последней буквы 'z'. Множество доступных букв еще сократится, теперь это будут буквы, находящиеся правее самой правой из букв 'z' и 'y'. Продолжаем так, пока не выпишем все подходящие буквы.
Утверждение: ответ будет положительным тогда и только тогда, когда в бесконечном лабиринте существуют две различные достижимые из старта клетки, соответствующие одной и той же клетке оригинального маленького лабиринта. Действительно, если бесконечно далеко уйти можно, по пути точно придется посетить такие клетки. А если такие клетки существуют, придем в одну из них, и бесконечно будем идти по траектории, переводящей из первой во вторую.
Осталось проверить наличие таких клеток. Запустим поиск в глубину по бесконечному лабиринту из стартовой точки. Пусть он при посещении точки (x, y) сохраняет в visit[x%n][y%m] значение (x, y). Теперь если поиск пытается прийти в клетку (x, y) такую, что в visit[x%n][y%m] уже что-то есть, причем оно не равно (x, y), значит две требуемые клетки найдены — клетка (x, y) и та, что сохранена в visit[x%n][y%m]. Отметим, что этот поиск посетит не более nm + 1 клеток (принцип Дирихле). Асимптотика решения — O(nm).
Т.к. никакие три точки не лежат на одной прямой, решение всегда существует.
Сначала подвесим дерево за какую-нибудь вершину и dfs-ом посчитаем размеры всех поддеревьев. Теперь будем рекурсивно строить ответ. Найдем самую левую нижнюю точку и поставим ей в соответствие корень дерева. Ничего плохого от этого не случится, ведь эта точка — крайняя в множестве. Отсортируем все остальные точки по углу относительно этой самой левой нижней точки. Теперь пусть размеры поддеревьев корня равны s1, s2, ..., sk. Запустим алгоритм рекурсивно, передав первому поддереву корня первые s1 точек (в уже отсортированном порядке), второму поддереву — следующие s2 точек после первых s1, ..., последнему поддереву — последние sk точек. Легко видеть, что ребра, принадлежащие разным поддеревьям, в этом случае не будут пересекаться. На каждом этапе рекурсии надо сопоставлять самую крайнюю из выбранных точек с корнем поддерева и сортировать все остальные точки относительно нее. Тогда никакие два поддерева не будут иметь попарно пересекающихся ребер. Асимптотика решения —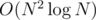 
.
196D - Следующая хорошая строка
Сразу заметим, что нас интересует только наличие подпалиндромов длины d и d + 1: любой подпалиндром большей длины будет содержать их, а если нет длины d и d + 1, нет и больших. Назовем их, для краткости, плохими.
Сначала найдем самую левую позицию pos, в которой символ строки точно нужно увеличить. Если плохих подпалиндромов нет, это будет конец строки (так как нужно найти хорошую строку, строго большую данной), иначе это самая левая позиция среди всех концов плохих палиндромов.
Увеличим s[pos]. Продолжим увеличивать, пока s[pos] является концом плохого палиндрома. Если пытаемся увеличить символ 'z', значит надо переходить к увеличению предыдущего символа. Если таким образом дошли до начала строки и увеличивать некуда, решения нет. Заметим, что при этом будет выполнено не более O(n) операций увеличения.
Пусть теперь pos — позиция самого левого измененного символа. Мы знаем, что префикс s[0..pos] не содержит плохих палиндромов. Теперь суффикс s[pos + 1..n - 1] можно заполнить жадно, перебираем позицию i по возрастанию, полагаем s[i] = 'a', и увеличиваем s[i], пока он является концом плохого палиндрома. Несложно понять, что на роль любого символа суффикса подойдет один из символов 'a', 'b' или 'c' — так как каждой позиции могут "помешать" лишь два символа находящихся левее на d и d - 1 позиций.
Таким образом, мы получили алгоритм, который требует быстрого выполнения двух операций: изменение одного символа и запрос, является ли данная подстрока палиндромом. Это можно делать с помощью хешей и дерева Фенвика.
Научимся узнавать хеш подстроки в изменяющейся строке. Тогда просто будем поддерживать информацию о самой строке, и о ее развернутой копии. Для определения, является ли данная подстрока палиндромом, просто сравним ее хеш с хешем соответствующей подстроки в развернутой версии.
Итак, пусть дерево Фенвика поддерживает величины h[i] = s[i]Pi, где P — простое число, используемое для хеширования. Тогда хеш подстроки s[L..R] равен (h[L] + h[L + 1] + ...h[R])P - L. (Разумеется, можно не домножать на P - L а просто при сравнении хешей домножать один из них на нужную степень) Если требуется изменить s[i] на c, прибавляем Фенвиком в i-ую позицию число (c - s[i])Pi.
Существует более быстрое решение, без хешей и структур данных, оно будет опубликовано немного позже.
Сперва заметим, что если порталы расположены во всех вершинах графа, то ответ — сумма длин ребер в минимальном остовном дереве, которое можно найти алгоритмом Краскала. Это довольно очевидно.
Однако порталы расположены не во всех вершинах. Попробуем это исправить.
Сделаем небольшой предпросчет: запустим алгоритм Дейкстры одновременно из всех порталов. Таким образом можно посчитать 2 массива: d[i] — расстояние от вершины i до ближайшего портала, и p[i] — ближайший к вершине i портал.
Теперь рассмотрим выполнение алгоритма Краскала на графе, состоящем только из порталов. На первой итерации этот алгоритм выберет ребро с минимальным весом среди всех ребер, соединяющем порталы. Только в исходном графе это могут быть не только ребра, но и пути.
Пусть такой кратчайший путь — из портала x в портал y. Заметим, что можно найти путь не длиннее, такой, что p[i] на нем будет меняться ровно один раз. Действительно, p[x] = x, p[y] = y, значит, на кратчайшем пути хотя бы раз меняется значение p[i]. Пусть оно меняется на ребре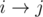 
, причем p[i] = x. Поскольку путь от j до p[j] — кратчайший путь от j до портала, путь 
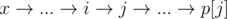не длиннее пути из x в y.
Тогда, т.к. p[i] = x, p[j] = y, можно рассчитать длину этого пути: она равна d[i] + w(i, j) + d[j] (w(i, j) — вес ребра (i, j)). Алгоритм Краскала прибавит эту величину к ответу и объединит порталы x и y. При этом объединятся поддеревья ближайших к ним вершин.
А теперь видим, что ничего не изменилось, и следующее по весу ребро можно найти точно таким же способом —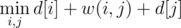 
. Если это ребро снова лежит между вершинами x и y, то DSU не даст посчитать это ребро, иначе это ребро соединяет другую пару порталов и войдет в ответ.
Как это считать. Из определения ребер в новом графе нетрудно понять, что их столько же, сколько и в исходном: каждому ребру (i, j) веса w(i, j) в старом графе соответствует ребро (p[i], p[j]) веса d[i] + w(i, j) + d[j] в новом графе. Поэтому построим новый граф и запустим на нем алгоритм Краскала — он посчитает вес минимального остовного дерева в графе, где вершины — порталы.
Осталось заметить, что если в стартовой вершине есть портал, то мы нашли ответ, а если нет — то надо сначала дойти до ближайшего портала, чтобы можно было начать считать миностов. Для этого можно просто в конце прибавить к ответу число d[1].
Thanks a lot! I suggest another simple solution for the 196A / 197C task. Scan the input string S from right-1 to left and add the character S[i] to the solution if it is larger than or equal to the previously added character. Initially, add the last character of S to the solution. Adding a character means appending it to the left side of the existing solution.
This is a really perfect idea. I've implemented it (1801617).
As an exercise: following this idea, calculate q ≤ 105 queries for a standard polynomial hash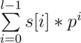
of the answer on substring s[i..j] (prime p is given).
i've no idea of your exercise,i think each query of the standard polynomial hash can be caculatored by O(j-i)(that i scan it from i to j). Could there be better solution like the problem C's solution?
Nice problem! I think we can sort the query first, and something like two pointers will work.
Sorry! Two pointers seemed doesn't work, we need a binary search, the total complexity is O(n*log(n)), can it be better?
nevermind
...of the answer on substring s[i..j]
I have a solution and I wonder if there's a simpler one. The solution is in rev. 1.
I also coded a similar solution using pairs here (1793816).
I am unable to understand this statement , Anybody please help me with this.
Answer is “Yes” iff there are two distinct, reachable from start position cells, which correspond to same cell in initial labyrinth.
There are two cells (x1, y1) and (x2, y2) satisfying these conditions:
D можно решать за линию хешами.
Решение по большому счету состоит из трех кусков.
1. Найти первый плохой. Ну тут и так за линию, если на отрезке хеш брать за 1.
2. Увеличить пока не убрались плохие. Тут можно заметить, что ля проверок нам нужны хеши, которые мы еще не трогали + 1 символ.
3. А дальше нам нужно уметь считать хеш на двигающихся вперед отрезках длины d-1 и d-2, приписывая символы. Ну и прямой и обратный хеш пересчитываются.
Правда по реализации получается страшнее, длиннее и запутаннее.
У меня совсем не запутанно. Поддерживаю префиксные хеши и префиксные хеши с обратным показателем степени (вместо P^i P^(n-i-1)). При изменении i-го символа достаточно элементарным образом пересчитать хеши на префиксе длины i+1. Ну и не смотреть в хеши правее измененного символа, не изменив следующие символы тоже. Код http://mirror.codeforces.com/contest/196/submission/1792911 (не сдается, потому что нет откатов, когда никакой символ не подходит).
D можно решать без хешей за линию Z-подобным алгоритмом поиска палиндромов. Идея: давайте запустим этот алгоритм и, как только какой-то символ нам не подходит, поменяем его и откатимся в алгоритме до первого использования этого символа. За счет амортизации это будет линия.
Div.2 A была в передаче "Настоящие аферисты" ("The Real Hustle"), где они в ресторане разводили людей на выпивку этим "трюком" :D
Есть еще более простой способ решать С div2, A div1 по-моему. Идти по строке, складывать в стек символ. Если тот, который мы хотим положить больше того, который там сверху лежит, то удаляем символы из стека до тех пор, пока текущий символ не станет меньше либо равным, чем тот, который в стеке сверху
Теперь в стеке осталась именно та последовательность, которая нам нужна
Можно, наверное, даже не класть в стек первый символ перед циклом.
Ну да, можно не класть, просто я хз зачем положил на контесте, а сейчас скопировал
Вопрос по задаче B — Бесконечный лабиринт. Подскажите, пожалуйста, как проверить (x1 ≠ x2 or y1 ≠ y2). Хранить массив, который помнит координаты точек, где мы прошли, тратит много памяти и можно легко вылезти за его пределы.
Не так надо хранить. Надо для каждой точки исходного лабиринта (их nm штук) хранить точку (x, y), которая проецируется на точку (x%n, y%m) и которую мы посещали. Либо вместо точки хранить смещение, на сколько лабиринтов ушли по отношению к исходному (вот мое решение: http://pastebin.com/SNXgWNne).
+1. Спасибо большое. Без Вас я бы не догадался до хранения смещения. Ещё раз спасибо.
UPD: разобрался, сдал задачу.
How do you get that solution for Paint Tree to run in time? My implementation, http://mirror.codeforces.com/contest/196/submission/1809672, keeps getting TLE, and I don't know how to optimize it. Besides, O(n^2*logn) should be too slow for n=1500 shouldn't it?
Your angle_comp works too long. Try to rewrite it in a simple way, not using cmath library. I got the same trouble 1810718, but then I rewrote operator< for points and it passed! 1810730
I have one other idea for 196C:
we have DFS function like this:
set point[1]:the most lower left point. and set point[1512].x=-10^9-7,point[1512].y=point[1].y.
set flag[point[1]]=true;
call DFS(1,1512);
and then answer is ready with O(N^2). but a little problem is here, my code gets WA!! link
why? help me please.
In problem B (Division 1) or problem D (Division 2):
Why does using set give TLE? The size of the set is $$$O(nm)$$$.
MLE-> 85574647 AC-> 85576009
Video tutorial for Div1A, Link: https://youtu.be/AH8za0dvSu8