If first player can't make first move (table is too small and plate doesn't fit it, i.e. 2r > min(a, b)), second player wins. Else first player wins. Winning strategy for first player: place first plate to the center of table. After that he symmetrically reflects moves of second player with respect to center of table. If second player has move, first player has symmetrical move, too. If not, first player won.
From math lessons we know, that only higher degrees of polinomials matter in this problem.
- If denominator degree is larger than numenator degree, answer is "0/1".
- If numenator degree is larger, answer is infinity. But what is sign of this infinity? To get it consider signs of highest degree factors of polinomials. If they are same, answer is positive infinity, else — negative infinity.
- If degrees of numenator and denominator are equal, answer is
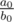 . To get irreducible fraction, you should divide this numbers by gcd(a0, b0). And don't forget that denominator of answer must be positive.
. To get irreducible fraction, you should divide this numbers by gcd(a0, b0). And don't forget that denominator of answer must be positive.
196A - Lexicographically Maximum Subsequence
Solution is greedy. First, write all 'z' letters (if there is any) — answer must contain them all for sure. Now it's time for 'y' letters. We can use only those of them which are on the right of last used 'z' letter. Then write 'x' letters — they must be on the right of the last used 'y' and 'z' letters. And so on.
Answer is "Yes" iff there are two distinct, reachable from start position cells, which correspond to same cell in initial labyrinth.
Proof: If these cells exist, move to first of them, and infinitely repeat moves leading from first to second. On the contrary, if infinite far path exist, on this path we obviously can find such cells.
How to find out if they exist? Start DFS from initial cell. For each cell visited, let visit[x%n][y%m] = (x, y). Now, if DFS tries to go to cell (x, y), visit[x%n][y%m] contains something, and (x, y) ≠ visit[x%n][y%m], we found these cells: they are (x, y) and visit[x%n][y%m]. Notice that DFS will visit no more than nm + 1 cells (Dirichlet's principle). So the asymptotic is O(nm).
No three points are in the same line, so the solution always exists.
First, choose any one vertex as the root of tree. Find size of each subtree using dfs.
Then, we can build the answer recursively.
Put the root of tree to the most lower left point.
Sort all other points by angle relative to this lower left point.
Let us name the sizes of subtrees of the root as s1, s2, ..., sk.
Run the algorithm recursively, giving first s1 points (in sorted order) for the first subtree of root, next s2 points for the second subtree and so on.
Obviously, no two edges from different subtrees can intersect now.
At each step of recursion we are to put the root of current subtree to the first point in sorted-by-angle order, and then sort other points by angle relative to it.
So, no two subtrees will have any intersecting edges.
The asymptotic of solution is 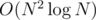 .
.
Notice, that only palindromes with length d and d + 1 matter. Any palindrome with greater length contains one of them. Let's call these palindromes bad.
First, find leftmost position pos, in which we surely should increase value of symbol. If there are no bad subpalindromes, pos = |s| - 1, else pos is leftmost position amongst all ends of bad palindromes.
Increase s[pos]. Increase it more, while s[pos] is end of bad subpalindrome. If you try increase 'z' symbol, you should proceed to increasing previous symbol. If this way you reached situation when you need to increase first symbol, and it is 'z', answer is "Impossible".
Now, let pos be position of leftmost changed symbol. We know, that prefix s[0..pos] doesn't contain bad palindromes. Now we can greedily fill suffix s[pos + 1..length(s) - 1]: go over positions i in ascending order, assign s[i] = 'a', and increase it, while s[i] is end of bad palindrome. Obviously, any of suffix symbols will be 'a', 'b' or 'c'.
So we got algorithm, which requires fast implementation of next operations — assigning single symbol, and query: is given substring palindrome? You can perform this operations using hashes and Fenwick tree.
Let's learn, how to get hash of substring in dynamically changing string. If we can it, we will keep string s and it's reversed copy. For query of second type we just need to compare hashes of substring in s and hash of corresponding substring in reversed copy.
Let Fenwick tree store values h[i] = s[i]Pi, where P is the prime number used for hashing. Then hash of substring s[L..R] equals to (h[L] + h[L + 1] + ...h[R])P - L. For assigning s[i] = c, add value (c - s[i])Pi to h[i]. Both these operations Fenwick tree does in  .
.
Also we have faster solution without hashes and data structures, it will be published soon.
First of all, we can note that if each graph vertex is portal, the answer will be a sum of all edges' weights in MST (minimal spanning tree). We can find MST by using Kruskal's algo.
In this problem, not an every vertex is portal. Let's fix this.
Start with a precalculation. Run Dijkstra's algo from all the portals, simultaneously. We will get d[i] — a distance between vertex i and p[i] — the nearest portal to vertex i.
Let's trace Kruskal's algo on a graph of portals. On the first iteration, it will choose the edge with the minimal cost, i.e. a shortest path between all the portals in the original graph.
Let the path leads from portal x to portal y. Note that there exists a path with the same length such as p[i] changes only once through it. Indeed, p[x] = x, p[y] = y, i.e. p[i] changed on the path. If it happens on edge 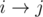 , p[i] = x, a path
, p[i] = x, a path 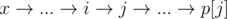 will not be longer than the path from x to y.
will not be longer than the path from x to y.
As p[i] = x and p[i] = y, we can see that the length of this path will be d[i] + w(i, j) + d[j], where w(i, j) is the weight of edge (i, j). Kruskal's algo will add this value to the answer and merge portals x and y. The shortest-path trees of vertexes x and y will also be merged.
Note, that almost nothing changed. The next edge for Kruskal's algo can be find in a similar way — 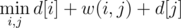 . If this edge connects x and y again, DSU makes us not to count this edge, otherwise this edge connects a different pair of edges and will be counted in an answer.
. If this edge connects x and y again, DSU makes us not to count this edge, otherwise this edge connects a different pair of edges and will be counted in an answer.
We can easily implement this. Just create a new graph of portals, with an edge (p[i], p[j]) of weight d[i] + w(i, j) + d[j] for every edge (i, j) of weight w(i, j) from original graph and run Kruskal's algo.
Finally, note that if the starting vertex is not a portal, we shall add d[1] to the answer.











Thanks a lot! I suggest another simple solution for the 196A / 197C task. Scan the input string S from right-1 to left and add the character S[i] to the solution if it is larger than or equal to the previously added character. Initially, add the last character of S to the solution. Adding a character means appending it to the left side of the existing solution.
This is a really perfect idea. I've implemented it (1801617).
As an exercise: following this idea, calculate q ≤ 105 queries for a standard polynomial hash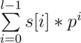 of the answer on substring s[i..j] (prime p is given).
of the answer on substring s[i..j] (prime p is given).
i've no idea of your exercise,i think each query of the standard polynomial hash can be caculatored by O(j-i)(that i scan it from i to j). Could there be better solution like the problem C's solution?
Nice problem! I think we can sort the query first, and something like two pointers will work.
Sorry! Two pointers seemed doesn't work, we need a binary search, the total complexity is O(n*log(n)), can it be better?
nevermind
...of the answer on substring s[i..j]
I have a solution and I wonder if there's a simpler one. The solution is in rev. 1.
I also coded a similar solution using pairs here (1793816).
I am unable to understand this statement , Anybody please help me with this.
Answer is “Yes” iff there are two distinct, reachable from start position cells, which correspond to same cell in initial labyrinth.
There are two cells (x1, y1) and (x2, y2) satisfying these conditions:
How do you get that solution for Paint Tree to run in time? My implementation, http://mirror.codeforces.com/contest/196/submission/1809672, keeps getting TLE, and I don't know how to optimize it. Besides, O(n^2*logn) should be too slow for n=1500 shouldn't it?
Your angle_comp works too long. Try to rewrite it in a simple way, not using cmath library. I got the same trouble 1810718, but then I rewrote operator< for points and it passed! 1810730
I have one other idea for 196C:
we have DFS function like this:
set point[1]:the most lower left point. and set point[1512].x=-10^9-7,point[1512].y=point[1].y.
set flag[point[1]]=true;
call DFS(1,1512);
and then answer is ready with O(N^2). but a little problem is here, my code gets WA!! link
why? help me please.
In problem B (Division 1) or problem D (Division 2):
Why does using set give TLE? The size of the set is $$$O(nm)$$$.
MLE-> 85574647 AC-> 85576009
Video tutorial for Div1A, Link: https://youtu.be/AH8za0dvSu8