It was enough interesting problems, I suggest discuss some of them. Who has proofed solutions of E and H?
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
38:21:52
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
38:21:52
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 03:13:08 (j3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Where can we find the problems?
If you have the opencup login then here: link. Until I don't know, could I post statements here.
H: Let's find a dfs search forest (from some vertices in each connected component). If it contains a path of length k + 1, print it. Otherwise, color each vertex with it's depth in the corresponding dfs tree.
Any ideas for problem I?
I do not know which solution did you mean, but my solution is proved by design.
Let's start coloring vertices using dfs. Each time we'll try to find such color
Cthat is not used by neighbours, but color(C-1+K)%Kis used. When paint vertex in this colorCand remember neighbour with color(C-1+K)%Kas previous for current vertex.If we do not fail on such painting process, we have a graph's coloring. Otherwise, we failed on painting of some vertex
v. That does mean, it neighbours uses all the colors, including colorK-1(0-based), so there is adjusted vertexuwitch has colorK-1. Here is some simple path from vertexuwhich is constructed by walking to previous vertices, and it's length is not less thanK-1, so by adding edgeu->vwe have sought-for path with lengthK.Ребята! Подскажите, пожалуйста, как A решать? (div1) Падает на 29ом хоть убей
Нельзя бинарить ответ. Вроде это wa 29.
Да, мы это поздно поняли) Но как решать по-умному?
Dlya kazhdogo i nahodim samuiu levuiu j takuiu chto summa ot j do i men'she S. Eto delaesh derevom otrezkov.
В смысле нельзя? Наше зашло на бинпоиске.
1) Построим частичные суммы от правого края.
2) Затем построим такие индексы, которые идут от правого края и если двигаться по ним, то сумма увеличивается.
3) Потом переберём длину отрезка слева и бинпоиском по построенному на предыдущем шаге массиву найдём самую правую хорошую границу.
Во втором пункте для массива [2,4,-2,1,1] массив индексов будет [4,3,1,0]
Можно бинарить! Запомним максимумы частичных сумм. Тогда для длины LEN будем проверять есть ли последовательности >=LEN с суммой <=S. Как это проверить? Просто переберём: для [x, x+len) надо проверить PART[x+len] — MAX[x] <= S. Если это выполняется, то отрезок является суффиксом какой-то хорошей последовательности.
How to solve C?
Problem C:
Consider multigraph on n vertices (not 2n!).
Disjunction ([not]x[i] | [not]x[j]) is edge between vertices i and j.
The solution is recursion (backtracking with optimizations).
If value of any variable may be deduced, deduce it.
If there are to connected components, calculate it separately, multiply results.
Fix unknown variable of maximum degree and do 2 recursive calls.
Your may add memoization to speed up the solution.
Your may handle the case of "maximum degree is two" in polynomial time.
As I know, the first 3 ideas were enough to get OK.
P.S. T(n) ≤ T(n - 1) + T(n - 1 - maxDegree)
UPD: (4) implies (2) for components of size 1 (degree equal to 0)
I just used memorization only.
Even no (1) and no (2)?
I saw that (1) happens automatically and thought solution is good enough as it is. I did not realize that hueristics can actually reduce the exponent.
We used just 1 & 4.
E: Main idea: number of ways to divide subset only depends on count of vertices. We can use DP to calculate it for every size.
Let's find first pair in subset. Sort all possible pairs and iterate over them. We need to know number of ways with this fixed pair in order to choose, take this or not. Number of ways depends only on size of left and right subset. Find this pair and recursively solve at first for left and then for right subsets.
What about I? We had 2^32*const solution, it was too slow, like 45 seconds instead of 5
I've seen several "read a paper" problems in Open Cup but I've never solved it. How do you solve it?
Search, read, understand, and implement a 10-page paper during a contest looks overwhelming to me. Is it important to find an easy-to-read article? Do you know the algorithm beforehand? Are you actually very good at reading papers?
Could you please give a link to the paper?
According to wikipedia the fastest algorithm is O(1.2377n), but we don't have an access and maybe this is an overkill.
This paper looks simpler, but it says this is O(1.62n) but I'm not sure if this is fast enough.
This paper is fine. The algorithm presented there is even harder than needed, what I've successfully submitted looks like:
But I think that using such classical problems on a competition is a completely bad idea. All I had to do was to know that this problem is called #SAT (or sharp-SAT). Also, this particular problem is very hard to prepare, I'm not sure that it is possible to come up with reasonable tests for it.
By the way, it is one of the main counting problems that arise in CS, the #3SAT is actually a #P-complete problem, meaning that many counting problems may be reduced to it, like 0-1 matrix permanent, counting number of topological sorts of the DAG, counting number of correct k-colorings, and several others.
This one
http://mirror.codeforces.com/blog/entry/47641?#comment-319796
is not very hard to invent without any papers.
It works in 1.46n or 1.38n (if you handle the last case).
In practice it works faster.
To solve you have to know only one base idea "consider graph, take vertex of maximal degree".
P.S It's interesting to know, how many people used papers from google to get OK.
Please, "like" this comment,
if you read special papers during the contest, and got OK.
Please, "like" this comment,
if you did not used any special papers during the contest, and got OK.
173 people got OK?
Anyway, if we believe the ratio, it seems we should ignore the paper and solve it as usual.
Possible reasons: If you rating is high, your upvote gives more than +1. Also most teams consist of three members.
Lol, your upvote gives +2 at maximum, there are 3 members at a team and 19 teams that solved this problem, giving us 114 votes at maximum.
I believe there were lots of people who didn't even participate in opencup, but who like the idea of using or not using any papers in general, and who felt that it is fine to give their upvote for one of the options, even though they were not asked for it.
Despite the fact I've never solved, let alone attempted such a problem, I suppose it's more about having an eye for a particular algorithm, which usually means you have already implemented the said algorithm in the past at least once or twice, and all you need during the contest is a quick(?) rehearsal.
Отвечаю про задачу I (
shuffle-twiceи упрощённый вариантshuffle-againдля Div2). Отдельным комментарием, потому что вопросы на английском, а ответить я сейчас готов только на русском.Обозначим исходное состояние генератора как x0, а все последующие как x1, x2, x3, ....
Заметим, что за один
shuffleкаждое число участвует в одном обязательномswap-е: в тот момент, когда на него указывает индекс цикла. При этом число перемещается на неотрицательное расстояние влево. После этого число может попасть в другиеswap-ы, каждый из которых перемещает его на положительное расстояние вправо.Сначала решим задачу
shuffle-again(Div2-версию): как восстановитьseedпосле одного вызоваshuffle. Легко понять, что последнее число участвует ровно в одномswap-е. Поэтому его позиция позволяет нам установить x10000·10000 div 232. Более того, если мы обратим последнийswap, то по аналогичным причинам предпоследнее число участвовало ровно в одном из оставшихсяswap-ов, и мы можем узнать x9999·9999 div 232, и аналогично далее: x9998·9998 div 232, x9997·9997 div 232, ....Научимся по следующему состоянию генератора находить предыдущее: если xk + 1 = xk·a + c, то xk = (xk + 1 - c)·a - 1 (оба равенства — сравнения по модулю 232). Для этого нужно всего лишь обратить число a по модулю 232.
Заметим, что, если мы знаем x10000·10000 div 232, это оставляет нам всего около 232 / 10000 возможных вариантов для истинного значения x10000. Переберём их все. Для каждого будем вычислять x9999, x9998, ... и сразу проверять, что числа x9999·9999 div 232, x9998·9998 div 232, ... такие, как у нас получились. Для каждого значения x10000 мы либо пройдём все эти проверки, либо очень быстро (за 1-2 шага) найдём проверку, которая выдаст ошибку. Поэтому суммарное время перебора будет близко к 232 / 10000. Как только мы найдём такое x10000, для которого пройдём все проверки, соответствующее ему x0 и будет искомым значением
seed.Решим теперь задачу
shuffle-twiceс двойным перемешиванием. Теперь каждое число участвует не менее чем в двухswap-ах. Откуда вообще мы можем получить информацию? Нам хотелось бы найти число, которое редко двигалось — тогда, может быть, мы перебором сможем найти, как именно оно двигалось. Поэтому будем искать такие числа, которые участвуют ровно в двухswap-ах, а не больше. Можно экспериментально проверить, что таких чисел примерно 1 / 6 от общего количества.Будем рассматривать числа, начиная с конца перестановки. Пусть очередное число не меньше своего индекса, например, p9000 = 9876. Предположим, что число 9876 участвовало ровно в двух
swap-ах: в момент 9876 оно переместилось на позицию mid, а в момент 10000 + mid — на позицию 9000. Переберём все возможные значения mid от 9000 до 9876 включительно.При зафиксированном значении mid у нас есть два сравнения по модулю следующего вида (*):
x9876·9876 div 232 = mid,
x10000 + mid·mid div 232 = 9000.
Предположим, мы научимся быстро находить все решения такой системы - а при достаточно больших модулях 9876 и mid их обычно не больше пары сотен. Тогда все x0, соответствующие этим решениям, являются кандидатами на правильное значение
seed. Проверять правильностьseedдля всех них может всё ещё быть долго, поэтому будем складывать x0 вsetи проверять только для тех, которые попали вsetво второй раз. Когда мы в переборе в первый раз найдём две верные гипотезы вида (*), проверка подтвердит правильность найденного x0, и мы сможем вывести ответ.Осталось научиться быстро решать систему из двух сравнений по модулю. Это задача по теории чисел, которую можно решать в два этапа: найти самое первое решение и по решению найти следующее. Обе части можно решить алгоритмом, строящим последовательные приближения и похожим на алгоритм Евклида.
Возможно, если хорошо организовать перебор на этапе поиска чисел, участвовавших ровно в двух
swap-ах, может хватить и медленного решения системы двух сравнений: перебора решений одного сравнения за 232 / mid и проверки, подходят ли они по второму сравнению.Разве на n-ом вызове range(k) не возвращает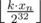 ?
?
Тогда получаются уравнения вида
Да, я тоже решаю эту систему переходом к отрезкам [l1, r1] и [l2, r2] по модулю 232 для двух некоторых xi. А потом ищу минимальные положительные шаги иксом первого отрезка, которые дают шаг на втором отрезке от - (r2 - l2 + 1) до - 1 и шаг от + 1 до + (r2 - l2 + 1).
Вот код, этот кусок решения в строках 175-199.
Я понял со второго раза. Действительно, не mod k, а ·232 div k везде. Спасибо, исправил.
На контесте мы написали точно такое же решение за исключением решения системы — оно было написано втупую за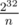 и, естественно, не зашло.
и, естественно, не зашло.
В итоге решение системы свелось к пересечению арифметической прогрессии по модулю и отрезка. Его можно найти за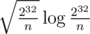 методом а-ля baby-step-giant-step(можно ли решить эту задачу быстрее?). После замены mapы для хранения кандидатов на хэштаблицу, решение со скрипом влезло в 3 секунды.
методом а-ля baby-step-giant-step(можно ли решить эту задачу быстрее?). После замены mapы для хранения кандидатов на хэштаблицу, решение со скрипом влезло в 3 секунды.
How to solve G?
Just try to randomly generate some sets with sizes 10..1e7 and look at the min/max/avg value of distinct_values/total_asked_values (hint: it's better to ask 10_000 values).
Then you'll able to find the answers and insert it to the main program.
My solution used Birthday Paradox. That is, the number of questions until two cards repeat is somehow close to sqrt(n), where n is the size of the set.
Let's do the following procedure: while I still have questions, ask questions until two cards are identical. Then, store in a vector number of question asked and repeat.
All numbers from my vector should be close to a value of sqrt(n), where n is in the set {10, 100, ...., 10^7}. The only remaining part is to find n such as numbers from my vector match best sqrt(n).
Let's iterae over powers of 10 and call X = sqrt(current number). We simply need to find an heuristic to see how close are number from the vector to X. We used sum {(vector[i] — X) ^ 2}
Then, pick X such as the sum is minimized and output corresponding power of 10.
I used Bayes formula and returned sets size with maximum probability (using uniform distribution over allowed values as prior).
Had solved stringy problem 'J' (about timer) with Perl, 127 lines (ideone).
Anyone know how to solve problem I?
The main ideas are described in Petr's blog:
http://petr-mitrichev.blogspot.com/2016/11/an-unshuffle-week.html
Thanks so much!!!!