В этой задаче было дано поле размером n × m и k запросов. Каждый запрос –-- это клетка поля. Нужно было для каждого запроса находить ближайшую к заданной не занятую клетку (при этом ближайшая клетка находится по манхэттенской метрике). После этого найденная клетка помечалась как занятая. В задаче предполагалось решение за время 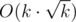 . Сначала поясним идею решения, затем покажем, как достигается такая временная оценка. Идея решения состоит в следующем. Прежде всего, если n > m, то повернем матрицу на 90 градусов (далее будет пояснено зачем). Будем хранить две матрицы n × m, в которых для каждой клетки будем хранить ближайшую свободную клетку слева и справа. Пусть теперь приходит запрос клетка (x, y). Будем перебирать величину d на сколько строчек мы отступим вниз и вверх. Когда мы зафиксировали d, то рассмотрим строку, например, x–d (аналогичные действия нужно будет проделать для строки x + d). В данной строке найдем при помощи наших матриц ближайшие свободные клетки слева и справа от клетки (x–d, y) и попробуем улучшить ответ. В тот момент, когда величина d станет больше, чем текущая найденная величина ответа, остановимся, т.к. в этом случае ответ уже не улучшится. После того, как мы найдем ответ на запрос – ближайшую клетку, нужно пересчитать значения в массивах. Это можно делать, используя, например, для каждой строки структуру DSU.
. Сначала поясним идею решения, затем покажем, как достигается такая временная оценка. Идея решения состоит в следующем. Прежде всего, если n > m, то повернем матрицу на 90 градусов (далее будет пояснено зачем). Будем хранить две матрицы n × m, в которых для каждой клетки будем хранить ближайшую свободную клетку слева и справа. Пусть теперь приходит запрос клетка (x, y). Будем перебирать величину d на сколько строчек мы отступим вниз и вверх. Когда мы зафиксировали d, то рассмотрим строку, например, x–d (аналогичные действия нужно будет проделать для строки x + d). В данной строке найдем при помощи наших матриц ближайшие свободные клетки слева и справа от клетки (x–d, y) и попробуем улучшить ответ. В тот момент, когда величина d станет больше, чем текущая найденная величина ответа, остановимся, т.к. в этом случае ответ уже не улучшится. После того, как мы найдем ответ на запрос – ближайшую клетку, нужно пересчитать значения в массивах. Это можно делать, используя, например, для каждой строки структуру DSU.
Покажем теперь, почему данное решение работает за время 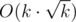 . Предположим, у нас все запросы одинаковы, т.е. одна и та же точка (x, y). Тогда если поле достаточно большое, то все точки будут располагаться в виде квадрата, повернутого на 45 градусов, с центром в точке (x, y). При этом сторона квадрата будет иметь величину порядка
. Предположим, у нас все запросы одинаковы, т.е. одна и та же точка (x, y). Тогда если поле достаточно большое, то все точки будут располагаться в виде квадрата, повернутого на 45 градусов, с центром в точке (x, y). При этом сторона квадрата будет иметь величину порядка 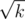 . Тогда и диагональ, которую мы рассмотрим в результате решения, описанного выше, имеет величину порядка
. Тогда и диагональ, которую мы рассмотрим в результате решения, описанного выше, имеет величину порядка 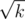 . Т.е. в каждом запросе мы рассматриваем
. Т.е. в каждом запросе мы рассматриваем 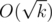 строчек и в каждой строке мы совершаем O(1) действий. Если поле такое, что квадрат не помещается в него, т.е. слишком узкое либо по вертикали, либо по горизонтали, то получится нечто, похожее на прямоугольник, у которого одна из сторон будет меньше
строчек и в каждой строке мы совершаем O(1) действий. Если поле такое, что квадрат не помещается в него, т.е. слишком узкое либо по вертикали, либо по горизонтали, то получится нечто, похожее на прямоугольник, у которого одна из сторон будет меньше 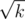 . Тогда повернем поле таким образом, чтобы меньшая сторона этого прямоугольника соответствовала строкам. В результате мы будем проходить при каждом запросе также не более
. Тогда повернем поле таким образом, чтобы меньшая сторона этого прямоугольника соответствовала строкам. В результате мы будем проходить при каждом запросе также не более 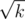 строк и в каждой строке совершать не более O(1) действий. Данная задача предполагалась как самая сложная задача контеста.
строк и в каждой строке совершать не более O(1) действий. Данная задача предполагалась как самая сложная задача контеста.
Данная задача являлась самой простой задачей контеста. В ней необходимо было найти среднее арифметическое заданных чисел. С задачей справилось подавляющее большинство участников соревнования.
В задаче было задано описание группового этапа некоторого футбольного соревнования, и правила подсчета очков и выявление победителей. Были даны результаты всех матчей, кроме одного и требовалось найти наиболее подходящий исход матча, удовлетворяющий некоторым критериям, при котором команда Берляндии занимала бы первое или второе место в своей группе.
Для решения задачи достаточно было заметить, что поскольку в каждом из уже сыгранных матчей было забито не более 18 голов, то можно перебрать исход последнего матча, при котором забито не более 200 голов и найти наиболее подходящий. Проще всего было при фиксированном исходе заполнить таблицу до конца (т.е. изменить значения очков и забитых мячей для команд, играющих последний матч), а затем отсортировать команды в соответствии с заданными правилами и проверить, что команда Берляндии попала в первые две лучшие команды группы.
В данной задаче был дан набор шаблонных функций своими названиями и списками параметров (при этом мог использоваться обобщенный тип), список переменных и их типов и некоторое количество запросов. Каждый запрос описывает функцию, заданную также своим именем и списком параметров. Про каждую такую функцию нужно было сказать, скольким шаблонным функциям из набора она <<подходит>>. <<Подходит>> в данном случае означает, что у нее и функции из набора совпадают имена, количество параметров и сами параметры.
Для решения задачи нужно было просто реализовать то, что было описано в условии. Ограничения позволяли отвечать на каждый запрос за время, пропорциональное количеству шаблонных функций в наборе, поэтому нужно было перебрать функцию из набора и проверить совпадение имен и списков аргументов.
В данной задаче по сути было дано четыре числа c3, c4, c5, s. Нужно было найти такие числа 0 ≤ k3 ≤ k4 ≤ k5, что c3·k3 + c4·k4 + c5·k5 = s и при этом |c3·k3–c4·k4| + |c4·k4–c5·k5| минимально.
Для начала переберем k4 так, чтобы s–c4·k4 ≥ 0. Затем рассмотрим 4 случая, в зависимости от того, каковы по знаку значения под модулями.
Рассмотрим случай c3·k3–c4·k4 ≥ 0 и c4·k4–c5·k5 ≥ 0. Тогда нужно минимизировать c3·k3–c5·k5. При этом 0 ≤ k3 ≤ k4 ≤ k5 и c3·k3 + c5·k5 = s–c4·k4. Рассмотрим диофантово уравнение c3·k3 + c5·k5 = s–c4·k4. При этом оно может не иметь решений. Рассмотрим случай, когда решения есть. Поскольку c3, c5 ≥ 0, то для минимизации c3·k3–c5·k5 нужно минимизировать k3 и максимизировать k5. Все решения диофантового уравнения c3·k3 + c5·k5 = s–c4·k4 можно выразить через один параметр k. Тогда необходимо найти отрезок значений k, при которых k3 будет подходящим, отрезок, при котором k5 будет подходящим, пересечь данные отрезки и, если пересечение не пусто, выбрать то значение k, при котором k5 максимально.
Аналогично рассуждая, нужно разобрать остальные 3 случая и выбрать оптимальные значения k3 и k5 для фиксированного k4. Можно было также заметить, что в каждом из случаев искомая функция линейно зависит от аргумента, а, значит, она принимает минимальное значение на отрезке в одном из его концов. Поэтому можно не рассматривать случаи, а находить отрезки k, при которых k3, k5 принимают допустимые значения, и считать целевую функцию в концах этих отрезков. Если при этом для всех фиксированных k4 не существует решений диофантовых уравнений, или пересечения выше указанных отрезков пустые, то ответ IMPOSSIBLE, иначе нужно выбрать лучшее. Таким образом решение получается за O(s·log(s)) --– перебор k4, и решение диофантова уравнения при каждом k4.











У меня одного в разборе по задаче Е формулы не так отображаются?
Не у одного тебя. Там есть кое-какой баг с тегами, я про него писал г-ну Мирзаянову, но он
мое сообщение проигнорировалпока не переписал парсер.I could not get after this line , All solutions of diofant equation c3· k3 + c5· k5 = s–c4· k4 can be described by using one argument k. Please help me understanding this line !
suppose we have diofant equation a·x + b·y = c and we have one solution (x0, y0), then we can describe all solutions as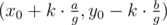 , where g = gcd(a, b)
, where g = gcd(a, b)
Thanks for editorial!
Suggestion: As I can see, you had written this 2 days ago but I was not able to find it in recent actions or in the main post of Round #126 introduction. Maybe it's better to update main article immediately after publishing editorial. Thanks in advance :-)
Sorry but, I think that your links are all linked to the "200A - Cinema" problem. Can you correct them? Thanks.
Thanks, fixed)