zscoder's blog

Atcoder Beginner Contest 046 / Atcoder Regular Contest 062
By zscoder, history, 8 years ago, In English

Contest link

Announcement

Start time : 21:00 JST as usual

Reminder that this contest actually exists on Atcoder :)

Let's discuss the problem after contest.

  • Vote: I like it
  • +53
  • Vote: I do not like it

Comments Comments (20)
| Write comment?
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by zscoder (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Me in the contest :

Finally got samples passed for E in 1 hr 33 mins! Submits. Thinks that it will finally get AC.

Verdict : TLE

-_-

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I got samples 1 and 3 pass ~2 minutes before the end. In 1 minute after the end I found that I forgot to remove debug "break" which prevented checking cubes whose smallest tile index is > 0. Though also getting TLE now after tests 16/20 :)

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it

    You had to be careful with your constant factors in this problem, I got TLE initially too.

    My algorithm was O(n2), and you might think it would be easy to pass with n < 400, but it's actually more like 45 * n2. Those bunch of rotations really add up...

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 5   Vote: I like it 0 Vote: I do not like it

      Just figured out my mistake: when I was checking for particular colour 4-tuples, the checks created keys with zero values in the map<Colors, int>, which I then iterated many times..

      Got AC with just 130ms.

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain how to solve task

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hint : Suppose at time i the ratio is x: y, then if a is the number of votes for A and b is the number of votes for B, then .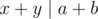

    → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    Maintain the minimum possible values of votes for both (t, a). Then on getting new ratio (T, A), you add minimum numbers (x, y) to those values such that they are divisible by the new ratio parts respectively (T and A). Then you need to make the following hold:

    dt = (t + x) / T = (a + y) / A = da

    (here dt = da is the gcd of real vote numbers which was removed during fraction simplification). Assume that dt > da. Then you simply add (dt - da) * A to y.

    AC

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it +6 Vote: I do not like it

      You have given the link for wrong question. Here is my code for the problem. Its given that T, A are co-prime. So if you are currently at (t, a) your next state would be (k.T, k.A) such that k is minimum, and k.T ≥ t and k.A ≥ a.

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I binary searched for the next pair of numbers with the correct ratio: http://arc062.contest.atcoder.jp/submissions/928173

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It wasn't really needed. I found the next pair in O(1).

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I know. It's one of the solutions that takes the least amount of thinking though.

        → Reply
»
8 years ago, # |
  Vote: I like it +28 Vote: I do not like it

Does anyone didn't get AC on problem E in contest just because print answer mod 10^9+7 like me...?

→ Reply
»
8 years ago, # |
  Vote: I like it +15 Vote: I do not like it

There is no editorial in english :(

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

How to solve problem F (Painting Graphs with AtCoDeer)? It seems interesting and I haven't the slightest clue on how to proceed with the solution. :)

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    You can check the japanese editorial by changing your language on AtCoder, but basically, unless the graph has no cycles or the graph is a single cycle, the described operation allows you to permute the colors however you want, so only the amount of each color matters. The two exceptional cases should be easy to solve separately.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Can you elaborate further?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        There's not much else to say, I guess I'll end up rewriting the same thing with different words.

        First, the edges in one biconnected component can't influence the others, so we can consider each one separately and multiply the answers. If the component is a single edge, then the number of configurations is trivially K. If the component is nothing but a cycle with n edges, then the answer is the number of necklaces with n beads and k colors.

        If the component is anything other than those two options, then the operations you have are actually powerful enough that you can rearrange the colors of the edges inside the component arbitrarily. This means that any two arrangements with the same number of edges of each color are equivalent, and you can count the number of different arrangements using stars and bars.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
          ← Rev. 2   Vote: I like it +3 Vote: I do not like it

          Oh by component you meant biconnected component. So each biconnected component can be treated separately because they partition the edges of the graph into equivalence classes where two edges are equal iff there is a cycle containing both edge.

          → Reply