Start time : 21:00 JST as usual
Reminder that this contest actually exists on Atcoder :)
Let's discuss the problem after contest.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
40:24:50
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
40:24:50
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 01:10:11 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Auto comment: topic has been updated by zscoder (previous revision, new revision, compare).
Me in the contest :
Finally got samples passed for E in 1 hr 33 mins! Submits. Thinks that it will finally get AC.
Verdict : TLE
-_-
I got samples 1 and 3 pass ~2 minutes before the end. In 1 minute after the end I found that I forgot to remove debug "break" which prevented checking cubes whose smallest tile index is > 0. Though also getting TLE now after tests 16/20 :)
You had to be careful with your constant factors in this problem, I got TLE initially too.
My algorithm was O(n2), and you might think it would be easy to pass with n < 400, but it's actually more like 45 * n2. Those bunch of rotations really add up...
Just figured out my mistake: when I was checking for particular colour 4-tuples, the checks created keys with zero values in the map<Colors, int>, which I then iterated many times..
Got AC with just 130ms.
Can someone explain how to solve task
Hint : Suppose at time i the ratio is x: y, then if a is the number of votes for A and b is the number of votes for B, then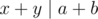
.
Maintain the minimum possible values of votes for both (t, a). Then on getting new ratio (T, A), you add minimum numbers (x, y) to those values such that they are divisible by the new ratio parts respectively (T and A). Then you need to make the following hold:
dt = (t + x) / T = (a + y) / A = da
(here dt = da is the gcd of real vote numbers which was removed during fraction simplification). Assume that dt > da. Then you simply add (dt - da) * A to y.
AC
You have given the link for wrong question. Here is my code for the problem. Its given that T, A are co-prime. So if you are currently at (t, a) your next state would be (k.T, k.A) such that k is minimum, and k.T ≥ t and k.A ≥ a.
Corrected, thanks. Your k is my dt.
I binary searched for the next pair of numbers with the correct ratio: http://arc062.contest.atcoder.jp/submissions/928173
It wasn't really needed. I found the next pair in O(1).
I know. It's one of the solutions that takes the least amount of thinking though.
Does anyone didn't get AC on problem E in contest just because print answer mod 10^9+7 like me...?
There is no editorial in english :(
How to solve problem F (Painting Graphs with AtCoDeer)? It seems interesting and I haven't the slightest clue on how to proceed with the solution. :)
You can check the japanese editorial by changing your language on AtCoder, but basically, unless the graph has no cycles or the graph is a single cycle, the described operation allows you to permute the colors however you want, so only the amount of each color matters. The two exceptional cases should be easy to solve separately.
Can you elaborate further?
There's not much else to say, I guess I'll end up rewriting the same thing with different words.
First, the edges in one biconnected component can't influence the others, so we can consider each one separately and multiply the answers. If the component is a single edge, then the number of configurations is trivially K. If the component is nothing but a cycle with n edges, then the answer is the number of necklaces with n beads and k colors.
If the component is anything other than those two options, then the operations you have are actually powerful enough that you can rearrange the colors of the edges inside the component arbitrarily. This means that any two arrangements with the same number of edges of each color are equivalent, and you can count the number of different arrangements using stars and bars.
Oh by component you meant biconnected component. So each biconnected component can be treated separately because they partition the edges of the graph into equivalence classes where two edges are equal iff there is a cycle containing both edge.