Since the official editorial is yet to be released and people are starting to ask for editorial, I decide to write this problem analysis and hopefully this may help the situation. =]
Sorry for my bad English if I made some grammatical mistakes.
732A. Buying a shovel
We could simulate the buying process — just buy until you can buy without change.
As the problem statement have already stated, you can always buy 10 shovels without change, so there is at most 10 iterations.
732B. Cormen — The Best Friend Of a Man
Iterate the days from left to right, and increase the days greedily on the right to fulfill the requirement. Take a look at this figure if you don't understand why this doesn't know why this works.
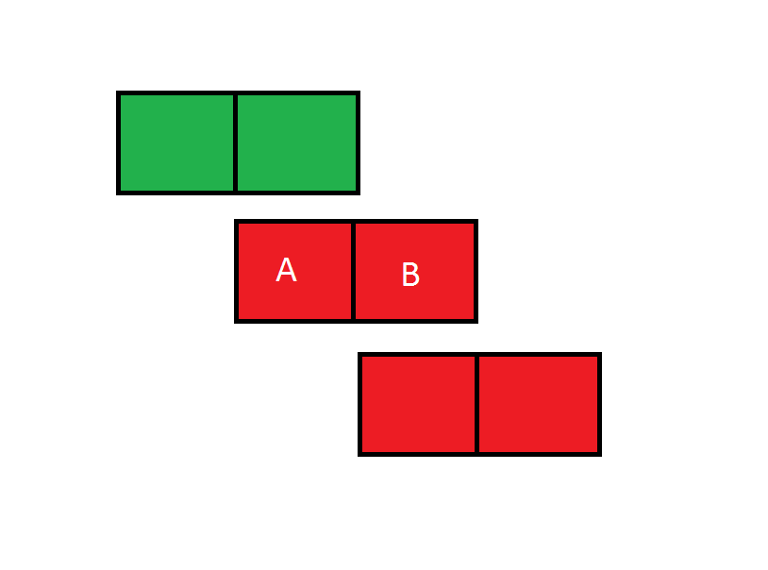
Let's say we are deciding to whether increase the days on A or B to make the total walks on those days become >= k. As we are iterating from left to right the blocks to the left are guaranteed to have already fulfilled the requirement. You can see that placing extra walks on day A will be less beneficial, as placing extra walks on day B could possibly help out the block day B and day B+1.
Time complexity: O(N)
732C. Sanatorium
Let's start from scratch, assume that we start and end our vacation before, what is the solution? Let MAX be the most ate meal throughout the vacation, we have to stay at least MAX days to eat enough meals, so the answer is 3*MAX — (sum of meals).
Now we come back to our question — how about if can start and end at anytime? With a little bit of imagination you can see that we could have an extra (or have one less) meal of any combination. As we have discovered before, the solution is 3*MAX — (sum of meals), so we have to greedily reduce the number of MAX to find out the minimal solution.
Time complexity: O(1)
732D. Exams
The major observation is that the solution is monotonic — if we can complete all the exam on day X, then we can always complete it using more than X days.
That means we can use binary search to search for the answer. The problem reduces to how to check if one can pass all the exam by day X. We can solve this problem by greedy — Sort all the subjects by the latest date you can take the exam, since we are only checking if you can pass all exams by day X, therefore it is always "safer" to take a late examination instead of an early one. Then, we check if there are enough days for revisioning and taking the examination.
If there is no solution in the range [1,n], print -1.
Time Complexity: O(N*logN*logM)
732E. Sockets
Define S{X} be the power achievable by adding adapters on a socket that has a power X. One could observe that if power Y is in the set S{X}, then S{Y} is a subset by S{X}. Secondly, you are going to use less or equal adapters if you use socket Y instead of socket X.
Using these observations, we can solve this problem by greedy (you should be familiar with it by now). Sort the power of the sockets from small to large, and add adapters on the sockets until you find a suitable computer. This guarantees we are using the least amount of adapters while plugging in the most amount of computers.
Time complexity: O(NlogN)
732F. Tourist Reform
We are going to break down the problem with these observations:
Each connecting components should be considered individually — It is obvious that cities that are not connected (directly or indirectly) are not going to affect each other's Ri value.
Each biconnected components could be grouped together — we won't have problem with reaching from city U to V and back to U if we create a cycle by the biconnected components.
Each biconnected components will also have other edges linked with it, and they will either become pointing inwards or outwards. As the biconnected components are not biconnected with other components (or else we will just group it), it is guaranteed that one of the biconnected components will have all it edges connecting to others pointing inwards.
The last observation is significant as it tells out that the solution for each connected component is the size of the largest biconnected component, as it is without doubt the best candidate to have all the edges pointing inwards to it. This also means that the solution is the minimum among all the connected components.
In order to find out the biconnected components you can use the Tarjan algorithm. I strongly recommend you to learn it if you haven't, and practice it on this question. 652E. Pursuit For Artifacts
The problem now reduces to how to allocate the direction of edges, from our observations we should allocate them in such way:
Build cycles in each biconnected components.
Make sure the largest biconnected components is the only one who has all edges pointing towards it in each connected components.
A simple way to complete the task is to initialize dfs from each largest biconnected components, and order the edges in revrese (i.e. from child to their parents).
Time complexity: O(N+M), O(N+MlogM) if you use maps to store the ID of each edge.










Auto comment: topic has been updated by haleyk100198 (previous revision, new revision, compare).