Hello everyone!
Here's an interesting problem. Sounds easy at first but I could not find a solution that matches experimental results. Maybe I am missing some simple observation.
You are given two integers 1 ≤ l1, l2 ≤ 2n. Consider two random subsets of n-bit vectors 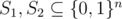 of sizes l1, l2 respectively. Let
of sizes l1, l2 respectively. Let
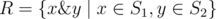 , where & is a bitwise AND.
, where & is a bitwise AND.
Compute the expected size of R (in polynomial in n time). Computing maximum possible size of R is interesting too.
An easier version is when bitwise AND is replaced by bitwise XOR, it is also interesting.
NOTE: I am not sure that this problem has a solution.











It really sounds very interesting so I'm going to think about it for a while. Just for the record, are you sure it is solvable? (like have you got it frome somewhere or have you just asked yourself whether you can compute it or not?)
No, I am not sure if it's solvable. This problem appeared in a research.
Best I can do with the "xor" case is .
.
First, let's select a fixed n-bit vector r. There are exactly 2n pairs of {x, y}, such that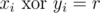 . Note that all xi (resp. yi) are distinct. Define the following function:
. Note that all xi (resp. yi) are distinct. Define the following function: 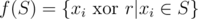 and observe that
and observe that 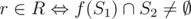 . In other words, to prevent r from being in R, we have to select whole S2 outside of f(S1).
. In other words, to prevent r from being in R, we have to select whole S2 outside of f(S1).
There are l1 elements in S1 and l2 elements in S2. For any set S1, there are exactly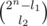 ways of choosing the set S2, such that the above intersection is empty, and thus
ways of choosing the set S2, such that the above intersection is empty, and thus 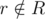 . There are exactly
. There are exactly 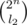 ways of selecting the set S2.
ways of selecting the set S2.
Combined together, we have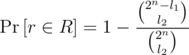 .
.
This yield an intermediate result, that (perhaps unsurprisingly), the expected size of R is 2n if l1 + l2 > 2n.
Otherwise, by linearity of expectation: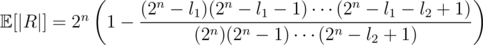 . Now I would speculate that you can only calculate that in time
. Now I would speculate that you can only calculate that in time  (you can of course use Stirling's formula to get some upper and lower bounds faster).
(you can of course use Stirling's formula to get some upper and lower bounds faster).
The "and" case is more complicated in the sense that the cardinality of set f(S1) is not constant, and I don't yet see a simple way of expressing it, but maybe someone will.
Ignore my post. I was wrong. :)
Linearity of expectation does not care about dependency actually.
I think majk meant l1 + l2 > 2n, becase in case of equality the numerator is equal to 1, not 0.
I just checked that from wikipedia. You are right. Good to know linearity of expectation applies even when the variables are not independent.
Thanks for correction hellman_, the inequality shall indeed be strict.
Exactly. You however need independence for linearity of variance.
First of all, the expected size of the set can be stated as: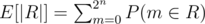 (by linearity of expectation [please confirm]).
(by linearity of expectation [please confirm]).
Let's now fix an element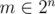 . Then
. Then 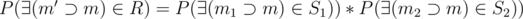 .
.
Now, the real answer can be computed via dynamic programming in O(3n) or O(2n * n). I now conjecture that you can reduce this to polynomial in n by making the rather intuitive observation that the answer depends solely on the number of set bits of m.
Could you elaborate on the DP part? Let n = 3. Then first we compute
How now to compute let's say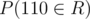 ?
?
By your formula we can compute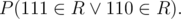
To get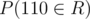 we also need to know
we also need to know 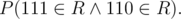
(I am using the equation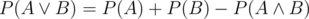 )
)
Going from the computed values to the required ones might be harder using probability notion. The good thing is you can always transform it into a counting problem (and vice-versa), and then normalize it accordingly.
Seeing it as a counting problem, you can just use a simple inclusion-exclusion principle and, by induction from DP, all the values of greater masks will be correct.
To reduce it to a polynomial problem you only need an easy observation: the probability for a number depends only on its number of 1s, letting you compute the dynamic programming in O(N). You would also need binomial coefficients to find out the answer which can be computed in O(N) as well so I guess that's all, isn't it?
PS: I consider the variant in which you have to compute the answer modulo a big prime number(like it's of the form P / Q and print P * Q ^ (-1)) because otherwise it still works but asking for precision for N a little bigger then 20 wouldn't work and with N small, you can backtracking for half of the values and it's much more interesting if you set N as 10^6
LE:The observation is right indeed, but the reccurence is not that simple actually so ignore most of what I said(except for the observation which should be relevant in any solution that uses those probabilities to compute the answer)
Does the original problem ask to compute the answer modulo some prime? Because, if not, computing the combinatorial probabilities might be pretty painful without some Gaussian approximations. If so, then a rather small modulo would solve the problem of computing large binomial coefficients. (remember that binomials in this problem contain a (2n)! term).
I suppose some maths theorem would be helpful for a bigger prime...