Всем привет!
Любители ли вы задачи, которые расчитаны на Ad Hoc решение? Я — терпеть не могу! Поэтому я решил сделать подборку идей, которые могут быть применены к достаточно большому классу задач. Добавляйте ещё, если о чём-то забыл. :)
1. Слияние множеств за 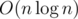 амортизированно. Если у нас есть некоторые множества, которые нам потом нужно будет соединять, поддерживая промежуточные результаты, то можно делать это в лоб, всегда добавляя меньшее множество к большему. Таким образом, каждый элемент будет перенесён в какое-то другое множество не более, чем
амортизированно. Если у нас есть некоторые множества, которые нам потом нужно будет соединять, поддерживая промежуточные результаты, то можно делать это в лоб, всегда добавляя меньшее множество к большему. Таким образом, каждый элемент будет перенесён в какое-то другое множество не более, чем 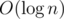 раз, так как новое множество для него каждый раз будет увеличиваться хотя бы в два раза. На этом, в частности, основана одна из версий общеизвестного DSU. Из применений — можно сливать множества внутри обхода дерева в глубину и таким образом можно для каждой вершины в какой-то момент времени подержать в руках множество всех элементов её поддерева.
раз, так как новое множество для него каждый раз будет увеличиваться хотя бы в два раза. На этом, в частности, основана одна из версий общеизвестного DSU. Из применений — можно сливать множества внутри обхода дерева в глубину и таким образом можно для каждой вершины в какой-то момент времени подержать в руках множество всех элементов её поддерева.
2. Подвохи в задачах. Часть 1. Ни для кого не секрет, что иногда авторы пытаются скрыть важные детали условия. Так, я однажды встретил в разделе input ограничения 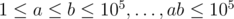 . И сразу и не скажешь, что на самом деле
. И сразу и не скажешь, что на самом деле 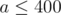 .
.
3. 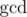 на подотрезках. Пусть у нас есть множество чисел, мы добавляем к нему элементы и после этого считаем
на подотрезках. Пусть у нас есть множество чисел, мы добавляем к нему элементы и после этого считаем 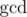 всех чисел множества. Тогда мы получим не более
всех чисел множества. Тогда мы получим не более 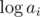 значений для него. отсюда следует, что можно следующим образом поддерживать в сжатом виде информацию о
значений для него. отсюда следует, что можно следующим образом поддерживать в сжатом виде информацию о 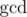 на всех подотрезках массива
на всех подотрезках массива 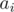 :
:
4. От статичного множества к расширяемому за 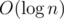 . Пусть для какого-то статичного множества мы умеем вычислять функцию, такую что
. Пусть для какого-то статичного множества мы умеем вычислять функцию, такую что 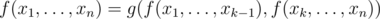 , где
, где 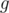 — функция, которую мы также можем быстро вычислять. Например,
— функция, которую мы также можем быстро вычислять. Например, 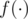 — количество элементов множества, меньших
— количество элементов множества, меньших 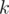 ,
, 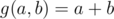 . Или
. Или 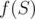 — количество вхождений строк из
— количество вхождений строк из 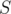 в строку
в строку 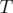 ,
, 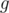 — всё ещё операция суммы.
— всё ещё операция суммы.
Ценой дополнительного 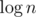 в асимптотике мы можем научиться добавлять в множество новые элементы и всё ещё уметь вычислять эту функцию. Для этого заведём
в асимптотике мы можем научиться добавлять в множество новые элементы и всё ещё уметь вычислять эту функцию. Для этого заведём 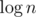 не пересекающихся множеств, дающих в объединении исходное и чтобы при этом размер
не пересекающихся множеств, дающих в объединении исходное и чтобы при этом размер 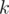 -го множества был равен либо
-го множества был равен либо  , либо
, либо 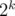 . Теперь при добавлении элемента добавим его в
. Теперь при добавлении элемента добавим его в  -ое множество и будем перестраивать все множества так, чтобы указанное ограничение выполнялось. Таким образом
-ое множество и будем перестраивать все множества так, чтобы указанное ограничение выполнялось. Таким образом 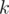 -ое множество будет потреблять
-ое множество будет потреблять 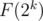 операций на каждые
операций на каждые 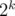 шагов, где
шагов, где 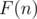 — стоимость построения множества из
— стоимость построения множества из 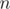 элементов с нуля, обычно что-то порядка
элементов с нуля, обычно что-то порядка 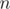 . Об этой оптимизации я узнал от Burunduk1.
. Об этой оптимизации я узнал от Burunduk1.
5.  -подмножества. Допустим, у нас есть множество чисел и мы хотим что-то узнать о том, что представляют собой исключающие или (xor) их подмножеств. Тогда мы можем представить числа как вектора в пространстве
-подмножества. Допустим, у нас есть множество чисел и мы хотим что-то узнать о том, что представляют собой исключающие или (xor) их подмножеств. Тогда мы можем представить числа как вектора в пространстве 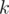 -мерных векторов над полем
-мерных векторов над полем 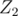 остатков по модулю 2. Оно интересно в частности тем, что в нём применимы основные алгоритмы линейной алгебры. Например, здесь показано, как, поддерживая базис в хорошем виде отвечать на запросы добавления нового вектора в множество и поиска k-го в порядке возрастания возможного xor подмножества элементов: link. (Задача от PrinceOfPersia с Hunger Games)
остатков по модулю 2. Оно интересно в частности тем, что в нём применимы основные алгоритмы линейной алгебры. Например, здесь показано, как, поддерживая базис в хорошем виде отвечать на запросы добавления нового вектора в множество и поиска k-го в порядке возрастания возможного xor подмножества элементов: link. (Задача от PrinceOfPersia с Hunger Games)
6. Циклы в графе как линейное пространство. Сопоставим каждому набору простых циклов в графе 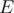 -мерный вектор линейного пространства на
-мерный вектор линейного пространства на 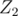 , у которого единица обозначает наличие соответствующего ребра в наборе. Можно ввести комбинацию циклов как сумму векторов в этом пространстве. Тогда можно показать, что множество циклов, получаемых добавлением одного ребра к дереву обхода в глубину будет содержать базис этого пространства. Комбинацию циклов можно трактовать как единый цикл, который проходит по рёбрам из вектора нечётное число раз, а по остальным — чётное, в такой интерпретации мы можем разложить любой не обязательно простой цикл на набор простых, а любой путь — на комбинацию простого пути и набора простых циклов. Это оказывается полезным если нас интересуют пути, в которых повторный проход по ребру аннулирует его вклад — например, если нас интересуют xor на путях. Пример задачи: 724G - Xor-матическое число графа
, у которого единица обозначает наличие соответствующего ребра в наборе. Можно ввести комбинацию циклов как сумму векторов в этом пространстве. Тогда можно показать, что множество циклов, получаемых добавлением одного ребра к дереву обхода в глубину будет содержать базис этого пространства. Комбинацию циклов можно трактовать как единый цикл, который проходит по рёбрам из вектора нечётное число раз, а по остальным — чётное, в такой интерпретации мы можем разложить любой не обязательно простой цикл на набор простых, а любой путь — на комбинацию простого пути и набора простых циклов. Это оказывается полезным если нас интересуют пути, в которых повторный проход по ребру аннулирует его вклад — например, если нас интересуют xor на путях. Пример задачи: 724G - Xor-матическое число графа
7. Алгоритм Мо. Вариант sqrt-декомпозиции. Не вдаваясь в подробности, основная идея в том, что если мы умеем неамортизированно добавлять элемент в множество (то есть, с возможностью отката), то мы можем разбить наш массив на группы по sqrt элементов, а запросы разбросать по блокам, в которых лежат их левые половины. Затем для каждого блока можно начать добавлять элементы с его границы и до конца массива. При этом, если мы наткнулись на правую границу запроса, добавим в множество элементы, которых не хватает до левой границы запроса, ответим на него, а затем откатим добавленные элементы.
8. Алгоритм Диница за 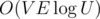 . Данный алгоритм за
. Данный алгоритм за 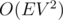 и без того летает на большинстве тестов. Однако, буквально двумя новыми строчками можно существенно улучшить его асимптотику. Для этого достаточно добавить к алгоритму идею масштабирования — перебираем сверху вниз некоторую степень двойки и, пока это возможно, рассматриваем только рёбра, веса которых не меньше, чем
и без того летает на большинстве тестов. Однако, буквально двумя новыми строчками можно существенно улучшить его асимптотику. Для этого достаточно добавить к алгоритму идею масштабирования — перебираем сверху вниз некоторую степень двойки и, пока это возможно, рассматриваем только рёбра, веса которых не меньше, чем 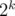 . Данная оптимизация и ведёт к озвученной асимптотике.
. Данная оптимизация и ведёт к озвученной асимптотике.
9. От расширяемого множества к динамическому за  . Пусть мы для некоторого множества умеем выполнять неамортизированную операцию добавления элемента и считать какие-то запросы. Тогда мы можем за дополнительный
. Пусть мы для некоторого множества умеем выполнять неамортизированную операцию добавления элемента и считать какие-то запросы. Тогда мы можем за дополнительный  времени научиться также обрабатывать в оффлайне запросы удаления из множества. Давайте для каждого добавления элемента x множества сопоставим момент, в который этот элемент покинет множество. То есть, определим для каждого элемента отрезок времени
времени научиться также обрабатывать в оффлайне запросы удаления из множества. Давайте для каждого добавления элемента x множества сопоставим момент, в который этот элемент покинет множество. То есть, определим для каждого элемента отрезок времени 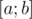 , на протяжение которого элемент присутствует в множестве. Теперь введём рекурсивную процедуру, обрабатывающую отрезок времени
, на протяжение которого элемент присутствует в множестве. Теперь введём рекурсивную процедуру, обрабатывающую отрезок времени 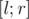 с тем условием, что когда мы в неё входим, в множество уже добавлены все элементы, отрезки которых целиком покрывают
с тем условием, что когда мы в неё входим, в множество уже добавлены все элементы, отрезки которых целиком покрывают 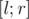 . Далее, поддерживая этот инвариант, мы рекурсивно запускаемся в половинки отрезка. Наконец, когда мы доберёмся до базы, отрезка длины 1, мы сможем выполнить запрос так, будто перед нами готовое статичное множество. Об этой идее мне также поведал Burunduk1, о чём я написал отдельный пост (про dynamic connectivity).
. Далее, поддерживая этот инвариант, мы рекурсивно запускаемся в половинки отрезка. Наконец, когда мы доберёмся до базы, отрезка длины 1, мы сможем выполнить запрос так, будто перед нами готовое статичное множество. Об этой идее мне также поведал Burunduk1, о чём я написал отдельный пост (про dynamic connectivity).
10. Линейные комбинации и матрицы. Часто, особенно в задачах динамического программирования нам нужно считать величину, которая является линейной комбинацией других величин. Что-то в духе 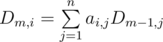 . В таких случаях мы можем записать коэффиценты
. В таких случаях мы можем записать коэффиценты 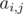 в матрицу
в матрицу 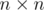 и воспользоваться бинарным возведением в степень. Таким образом мы сможем получить асимптотику
и воспользоваться бинарным возведением в степень. Таким образом мы сможем получить асимптотику 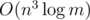 вместо
вместо 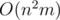 . Как мы видим, разница весьма существенна.
. Как мы видим, разница весьма существенна.
11. Оптимизация матричного возведения в степень. Допустим, есть матрица A размера 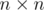 , и нам нужно часто вычислять значения
, и нам нужно часто вычислять значения 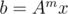 , где x — какой-то вектор. Наивное решение требовало бы от нас
, где x — какой-то вектор. Наивное решение требовало бы от нас 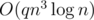 операций. Однако, мы можем заранее посчитать двоичные степени матрицы A, чтобы затем сделать
операций. Однако, мы можем заранее посчитать двоичные степени матрицы A, чтобы затем сделать  умножений матрицы на вектор, а не матрицы на матрицу. Тогда решение уже будет иметь асимптотику
умножений матрицы на вектор, а не матрицы на матрицу. Тогда решение уже будет иметь асимптотику 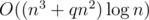 , что может оказаться существенным. Об этой идее в одном из своих комментариев поделился AlexanderBolshakov.
, что может оказаться существенным. Об этой идее в одном из своих комментариев поделился AlexanderBolshakov.
12. Магия эйлерова обхода. Рассмотрим такую задачу: дано дерево. Поступают запросы добавить число на поддереве и посчитать сумму на пути между заданной парой вершин. HLD? Как бы не так! Строим два обхода для дерева — в одном мы записываем сначала вершину, а затем её поддерево, а во втором наоборот — сначала поддерево, затем вершину. Можно заметить, что тогда разность префиксов из первого и второго обхода, включающих поддерево вершины v будет содержать исключительно те вершины, которые лежат на пути от неё к корню. Таким образом, задача сводится к прибавлению числа на подотрезке и сумме на префиксе. Эту идею мне рассказал Kostroma. Стоит также отметить альтернативное решение — хранить в каждой вершине дерева линейную функцию от её высоты и обновлять её у всех потомков вершины при запросе. Впрочем, оно, кажется, плохо обобщается.
13. Подвохи в задачах. Часть 2. Если дано k множеств, заданных явно списками, следует обратить внимание, что максимальное количество различных размеров таких множеств не превышает 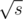 , где s — их суммарный размер. Имеет место также более сильное утверждение — не более
, где s — их суммарный размер. Имеет место также более сильное утверждение — не более 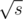 объектов имеют размер, превышающий
объектов имеют размер, превышающий 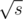 . Очевидный пример — когда нам даны несколько строк суммарной длины s. Менее очевидный пример — в разложении перестановки на циклы можно встретить не больше
. Очевидный пример — когда нам даны несколько строк суммарной длины s. Менее очевидный пример — в разложении перестановки на циклы можно встретить не больше  различных длин. Эта идея также имеет своё отражение в ряде теоретико числовых задач. Например, нам нужно посчитать что-то по всем числам, не превышающим большое число k, например,
различных длин. Эта идея также имеет своё отражение в ряде теоретико числовых задач. Например, нам нужно посчитать что-то по всем числам, не превышающим большое число k, например, 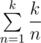 . Рассматриваем отдельно две группы чисел — числа, меньшие
. Рассматриваем отдельно две группы чисел — числа, меньшие 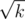 перебираем, а для остальных перебираем результат операции
перебираем, а для остальных перебираем результат операции  и считаем количество чисел, которые дадут такой результат целочисленного деления.
и считаем количество чисел, которые дадут такой результат целочисленного деления.
Ещё одно интересное следствие этой идеи — если в алгоритме Ахо-Корасик мы будем рассматривать пути до корня в дереве суффиксных ссылок, которые используют только вершины, являющиеся терминальными, то есть, соответствующие исходным строкам бора, то любой такой путь будет иметь длину 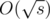 .
.
14. Convex hull trick. Пусть мы имеем некоторую динамику вида 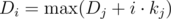 , то мы можем поддерживать выпуклую оболочку линейных функций, которые здесь имеются, а затем искать максимум с помощью тернарного поиска или бинарного поиска по углу вектора нормали к линейным функциям.
, то мы можем поддерживать выпуклую оболочку линейных функций, которые здесь имеются, а затем искать максимум с помощью тернарного поиска или бинарного поиска по углу вектора нормали к линейным функциям.
15. xor- and- и or- свёртки. Пусть у нас есть кольцо многочленов, в котором 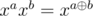 или
или 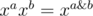 или
или 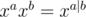 . Как и в обычном случае
. Как и в обычном случае 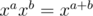 , можно научиться умножать такие многочлены порядка
, можно научиться умножать такие многочлены порядка 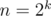 за
за 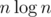 . Будем интерпретировать его как многочлен от
. Будем интерпретировать его как многочлен от 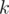 переменных такой, что каждая переменная входит в него со степенью не выше 1 и набор переменных при
переменных такой, что каждая переменная входит в него со степенью не выше 1 и набор переменных при 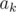 определяется двоичной записью числа
определяется двоичной записью числа 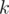 . Например, вместо
. Например, вместо 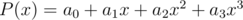 будем видеть
будем видеть 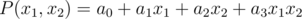 . Теперь заметим, что если рассматривать этот многочлен в вершинах куба
. Теперь заметим, что если рассматривать этот многочлен в вершинах куба 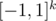 , то за счёт того, что
, то за счёт того, что 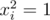 , получим, что при произведении двух многочленов в таких точках они будут сворачиваться именно согласно xor соответствующих номеров одночленов. or-свёртка получается аналогичным образом, но теперь мы рассматриваем значения в вершинах куба
, получим, что при произведении двух многочленов в таких точках они будут сворачиваться именно согласно xor соответствующих номеров одночленов. or-свёртка получается аналогичным образом, но теперь мы рассматриваем значения в вершинах куба 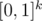 и потому имеем
и потому имеем 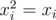 . and-свёртку предлагается додумать самостоятельно в качестве упражнения.
. and-свёртку предлагается додумать самостоятельно в качестве упражнения.
Напоследок замечу, что or-свёртка даёт в точности сумму по всем подмаскам, а также что обратное преобразование для xor-свёртки совпадает с исходным, за исключением того, что в конце нужно поделить всё на n. Спасибо Endagorion за то, что рассказал мне о такой интерпретации преобразования Уолша-Адамара.
16. Прямое и обратное FFT для двух многочленов одновременно. Пусть 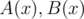 — многочлены с действительными коэффициентами. Рассмотрим
— многочлены с действительными коэффициентами. Рассмотрим 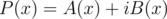 . Заметим, что
. Заметим, что 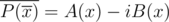 , откуда следует, что
, откуда следует, что 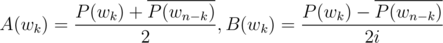 .
.
Теперь в обратную сторону — пусть мы знаем для многочленов 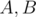 значения в корнях из единицы, а также знаем, что они имеют вещественные коэффициенты. Посчитаем обратное преобразование Фурье для
значения в корнях из единицы, а также знаем, что они имеют вещественные коэффициенты. Посчитаем обратное преобразование Фурье для 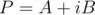 . Тогда, в силу линейности преобразования Фурье, коэффициенты для
. Тогда, в силу линейности преобразования Фурье, коэффициенты для 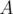 окажутся вещественной частью обратного преобразования, а коэффициенты
окажутся вещественной частью обратного преобразования, а коэффициенты 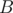 — мнимой.
— мнимой.
17. Произведение многочленов по модулю с вещественнозначным FFT. Если модуль большой, нам может не хватать точности. Чтобы этого избежать, разбиваем многочлены 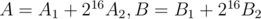 и считаем
и считаем 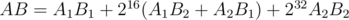 . С учётом предыдущего пункта, это делается за два прямых и два обратных FFT.
. С учётом предыдущего пункта, это делается за два прямых и два обратных FFT.
18. Хеширование структур. Чаще всего хеширование применяют к строкам (т.е., последовательностям), но хешированию также хорошо поддаются другие классы объектов — в частности, деревья и множества чисел. Так, например, множество чисел  можно хешировать многочленом
можно хешировать многочленом  . После этого объединению мультимножеств будет соответствовать сумма входящих хешей. Также можно, например, быстро пересчитать хеш для множества, ко всем элементам которого прибавили какое-то число, просто домножив хеш на основание в степени этого числа. Спасибо 300iq за то, что отметил это.
. После этого объединению мультимножеств будет соответствовать сумма входящих хешей. Также можно, например, быстро пересчитать хеш для множества, ко всем элементам которого прибавили какое-то число, просто домножив хеш на основание в степени этого числа. Спасибо 300iq за то, что отметил это.
Корневые деревья можно хешировать следующей известной процедурой: возьмём мультимножество хешей поддеревьев. Затем если такое множество уже встречалось ранее, присвоим вершине соответствующий множеству номер, иначе присвоим вершине и множеству новый номер. Для некорневых деревьев имеет место похожая процедура — просто нужно подвешивать их за центр или центроид.
Кстати, немного о том, почему хеши вообще работают, если кто-нибудь ещё не задумывался — у многочлена степени 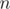 в поле может быть не больше
в поле может быть не больше 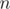 корней. Поэтому если из множества возможных аргументов мощности
корней. Поэтому если из множества возможных аргументов мощности 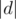 мы выбрали один, то вероятность того, что многочлены совпадают, но не равны тождественно (если точнее — их разность не равна тождественно нулю, но равна нулю в точке), не превышает
мы выбрали один, то вероятность того, что многочлены совпадают, но не равны тождественно (если точнее — их разность не равна тождественно нулю, но равна нулю в точке), не превышает 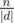 . Соответственно, если у нас есть
. Соответственно, если у нас есть 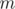 пар объектов, которых мы сравниваем, то вероятность того, что одна из проверок даст ложноположительный результат можно грубо оценить как
пар объектов, которых мы сравниваем, то вероятность того, что одна из проверок даст ложноположительный результат можно грубо оценить как 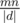 . Из этих соображений можно выбирать поле (остатков по модулю), в котором мы будем работать.
. Из этих соображений можно выбирать поле (остатков по модулю), в котором мы будем работать.
Также есть вариант использовать как хеш для одного числа не 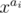 , а случайно выбранное число и всё ещё суммировать их. Кто-нибудь умеет оценивать вероятность коллизий в таком случае?
, а случайно выбранное число и всё ещё суммировать их. Кто-нибудь умеет оценивать вероятность коллизий в таком случае?










В комментариях к этому посту еще немного идей есть
кстати насчет FFT. Одна из классических оптимизаций — это умножение Монтгомери. Насколько я заметил, оно вообще не используется в олимпиадном программировании. Интересно, почему?
Ну я вот впервые слышу о нём, например. Что это такое и какие плюшки? :)
как написано на e-maxx,
если применить умножение Монтгомери, то модуль надо находить только в самом начале и в самом конце, а все промежуточные операции заменяются битовыми сдвигами. Собственно, в вики все написано: https://en.wikipedia.org/wiki/Montgomery_modular_multiplication
Вот кажется пост в тему: http://mirror.codeforces.com/blog/entry/5990
UPD: уже упомянуто в первом комменте
Ну первый комментарий же...
Потоки волшебные. Если в задаче достаточно маленькие ограничения, и вам кажется, что она похожа на какую-то ДПшку, но при этом уже час все ваши дпшки рушатся — попробуйте свести к потоку или минкосту.
Если в задаче просят разбить элементы на два множества как-нибудь — подумайте в сторону 2-SAT. Если при этом нужно минимизировать стоимость — подумайте в сторону минката.
Состоянием ДП может быть что угодно. Например, состояния работы какого-то алгоритма.
Простых чисел достаточно много и они встречаются часто.
что такое минкат и минкост?
Объясните, пожалуйста, поподробнее про хеширование корневых деревьев. Я не очень понял, в чем идея хранить для каждой вершины мультимножество.
Пусть поддеревья уже захешированы. Мультимножество их хешей однозначно задаёт дерево целиком. Поэтому можем сказать, что хеш всего дерева = хеш мультимножества хешей поддеревьев.
Моя интуиция подсказывает, что ты путаешь математическое понятие "мультимножество" с понятием "структура данных "мультимножество"".
Корневое дерево можно рекурсивно определить как пару из корня и мультимножества деревьев, подвешенных к корню. Тогда равенство двух деревьев, как ни странно, определяется через равенство этих пар (если мы не отличаем вершины друг от друга, то тогда достаточно сравнить мультимножества деревьев-потомков).
Соответственно, для корневых деревьев можно ввести классы эквивалентности и пронумеровать их целыми числами. В случае, когда у нас все вершины неразличимы, мы можем поддерживать
map<vector<int>, int>, где ключ — это вектор отсортированных номеров классов эквивалентности потомков корня, а значение — это класс эквивалентности всего дерева (к примеру, для листьев ключом будет пустой вектор). Собственно, для одного или нескольких деревьев этотmapлегко заполняется рекурсивным обходом.Автор поста же предлагает индексировать
mapне отсортированными векторами, а хэшами от оных векторов. Собственно, как их хэшировать, он уже рассказал (его алгоритм дает одинаковый хэш вне зависимости от порядка элементов в векторе).P.S. Опять-таки, я использовал
std::vectorиз C++ всего лишь как пример. На его месте вполне может быть обычный массив из Java с пользовательским компаратором. Может быть иstd::multiset. Может быть и что угодно другое.Да, именно это я и спутал. ))
Спасибо большое, стало намного понятнее.
Nice list! Could you clarify the 4th trick? What do we exactly want to calculate, and how does the trick help us?
For example, if f denotes the number of elements less than k and g(a, b) = a + b, does this mean that we want to calculate the number of elements less than k in the set? Why can't we just have a counter and increase its value by one if the new element is less than k?
It's solving "decomposable searching problems". I first saw the trick here.
Thanks! So apparently k is not a constant here.
For point 12 (Euler tour magic)
"We can see that difference between prefixes including subtree of v from first and second tours will exactly form vertices from v to the root"
I'm not really sure what this means. I know a subtree of v is a contiguous range in first tour but not sure what it means for the second tour.
It means the same for the second tour.
Just in the first way every time we "open" (enter) some subtree we write its root index down. In the second way we're writing down the moments when we "close" a subtree (left it/completely processed it).
So if you're looking at the prefix that contains some subtree of
uin both Euler's tours the difference between 2 prefixes are vertices whose subtree has been opened but not yet closed. And these vertices are parents ofu(= lie on the path from root tou)In what context is Euler Tour being mentioned in Point 12?
Isn't Euler Tour by definition supposed to include every vertex each time we visit it?
Then what does this line mean?
Let's consider two euler tours: in first we write the vertex when we enter it, in second we write it when we exit from itThis may be common knowledge, but it was mind-blowing to me when I first discovered it:
Avoiding re-initialization: Especially in graph-traversal or DP problems, you may be calling a subroutine multiple times, needing to initialize an array each time:
In cases where this re-initialization is the bottleneck of your program, or if your implementation is just slightly too slow to pass in time, it can be improved by using a sentinel and avoiding re-initialization each time:
The only change would be that instead of checking
visited[i] == -1, you would checkvisited[i] != sentinel. I used this trick recently in a problem where a BFS subroutine was to be called in every query. Changing thevisitedarray from boolean to int and using this trick helped me squeeze my solution into the time limit. Hope it helps!This is an optimization, but only a constant one. You could keep track of invalidated indexes in a vector (those i for which visited[i] became true) and reinitialize only these indexes. But your way is more convenient, of course.
Point 10: It should be O(n2log(m)), right?
UPD: Got it, it was mentioned using naive multiplication (n3). I was thinking about Cayley Hamilton Method (n2).
Can you elaborate on the method? If you're talking about this, it only applies for linear recurrences..
Anybody can provide example problems for these methods?
Some problems for first idea here: http://mirror.codeforces.com/blog/entry/44351
What about a blog have segment tree tricks?
What is the advantage of fourth method? Why can't I just use set?
PS. thanks for this excellent post
If I understand it well enough, it seems to me like the 4th point is also achievable with implicit key treaps. Operations on them are logarithmic (average case), they allow you to insert elements on any position and they can answer any range queries as long as the answer for a query of a subset can be computed quickly from the answers of the query of two of its subsets, which seems to be what point 4 is trying to achieve.
For #16, how do we compute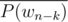 so that we can then compute
so that we can then compute 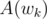 and
and 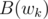 ?
?
I think we're supposed to compute the forward FFT of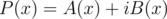 but I don't see how we get
but I don't see how we get 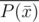 from that.
from that.
Sorry if this is simple, but I'm not able to see it.
Umgh, you know P(wn - k) so you just take conj(P(wn - k))
...Yep, it really was that simple. Thanks for your time.
Thanks a lot, man :). Really the tricks are so amazing, especially number 12. I have solved a problem using this trick. Problem link I will be grateful to u if u provide some problems that can be solved using trick 12. Thanks :)
prodipdatta7, Here you go.
Can anybody explain 3rd trick?
Decompose any number, say
n, into it's prime factors. Now when thegcdof the segment changes it must decrease by atleast half (Why? That's the least prime factor you can have). So there are atmostlog(A[i])+1different values.Can you explain it through an example please? Thanks for reply:)
How to prove statement in trick 13 "no more than
sqrt(n)sets have size greater thansqrt(n)" ?I am assuming $$$n$$$ is the sum of the sizes of all sets.
Suppose there are more the $$$\sqrt{n}$$$ sets with size greater the $$$\sqrt{n}$$$. Let $$$x$$$ be the sum of these sets, then $$$x > \sqrt{n} * \sqrt{n} = n$$$ which is a contradiction, because $$$x$$$ can not be greater than $$$n$$$.
#6 is called the cycle space. More details are in the Wikipedia article: https://en.wikipedia.org/wiki/Cycle_space
I am unable to understand Trick 1. Can anyone provide a better reference to understand Trick 1?
I doubt a grey guy could understand it anyway.
Well, I am here to clear your doubt that I understood it. Maybe I am slow but I do understand.
You should make a blog about it so others can understand.