=================================

Hello Codeforces, my name is C137 and as I said before, I will continue writing regularly in this blog:

It has been a long time since i wrote something new, because I was busy with some stuff, however I will try to post at least one topic every 10-15 days, and i am gonna select a problem that i really found it useful and interesting, and then i will talk about the way i solved this problem, with long editorial and analysis, by this way of sharing my thoughts i hope that grey, green and cyan contestants will benefit from it and learn something new, also i am hoping that top rated contestants will also add their notes to my solution, and suggest some more optimized code.

=================================

Today, I choose to you this graph problem, I hope you will like it:

P.S: if you are familiar with the basics of graph theory and the BFS algorithm, then i strongly recommend you to try with this problem at least for one hour before reading this blog:

Before I start, I would like to thank NourAlhadi and Samo.A.R for solving this problem after reading this blog, and adding his notes and suggestions to make it even more clear.

problem name: long journey

Link: here

type: Graphs

Difficulty level: Average

Short Description:

Given an un-directed un-weighted connected graph, two friends A and B stand in a starting node st, A wants to go to node en_a using the shortest possible path, similar B wants to go to node en_b using the shortest possible path, but they both want to share the maximum number of edges, your task is to calculate the maximum number of edges they will share.

Example:

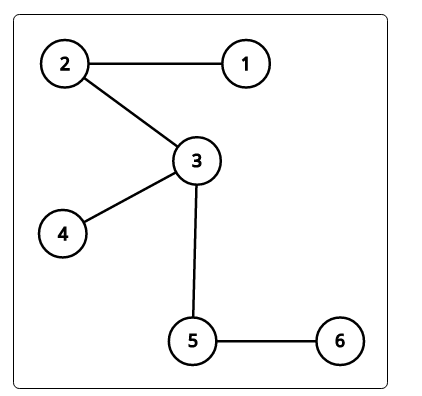
see the graph in the picture, let st be node 1, en_a be node 4 and en_b be node 6.

the optimal path for A will be 1 - 2 - 3 - 4

the optimal path for B will be 1 - 2 - 3 - 5 - 6

sharing two edges, from 1 to 2, and from 2 to 3.

Problem Analysis:

As a start we will make the following assuming, solve the problem based on it, then prove it's true:

the optimal path for A will be something like:

st - x₁ - x₂ - ...... - x_len - a₁ - a₂ - ..... - en_a

and the optimal path for B will be something like:

st - x₁ - x₂ - ...... - x_len - b₁ - b₂ - ..... - en_b

where nodes a₁, a₂, ...., en_a, b₁, b₂, ...., en_b are all distinct

that means, they will both start at node st, travel together till node x_len then separate, and never meet again.

but why this is true??? let's look at the two examples below:

in figure 1, the two friends should travel from node a to node e, there are two possible paths:

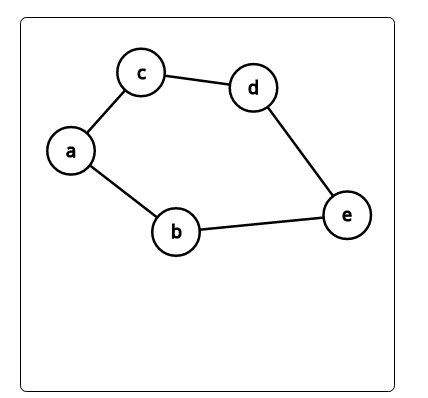
• a - b - e
• a - c - d - e

the optimal, is for them both to follow the first path, because it's the shortest, remember they both should take the shortest possible path.

in figure 2, the two friends should travel from node a to node f, there are two possible paths:

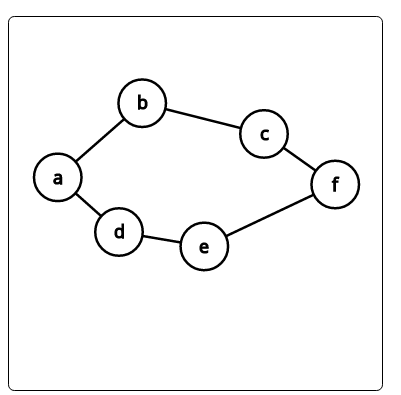
• a - b - c - f
• a - d - e - f

the two paths are in the same length, but it's better for them to choose the same path, to travel as much together as possible.

so it's clear, that if they are at any node, let's say x, and they will meet again at any other node, let's say y, then for sure all the nodes from the shortest path between x and y are part of the answer !!!

Now, we can say the answer is at a node x_len such that x_len is a part of a shortest path between st and en_a, and a part of a shortest path between st and en_b, and it's distance of st is maximum possible.

So, all we should do is make three BFS the first from node st store the distances in array dis1, second from node en_a store the distances in array dis2, third from node en_b store the distances in array dis3, then for each node x, we say:

if(dis1[x]+dis2[x]==dis1[en_a] && dis1[x]+dis3[x]==dis1[en_b] )ans=max(ans,dis[x]);

remember, if you want to check if a node x, is a part from the shortest path between nodes st and en, then run two BFS, and check whether dis1[x]+dis2[x]==dis1[en]

the time complexity for this code is a simple BFS and it's O(n + m), and the space complexity is O(n).

=================================

This is all I can say for this problem, I hope you liked my analysis and you benefit from it, I am not gonna post my code, because I think you can code it now after reading the analysis, If there is still something unclear, then fell free to ask me in the comments below, or send me a message...

I will try to post the next blog about the next problem in the following 10-14 days... Happy coding, and have a nice day :D

=================================