GSS4.
Собственно, нужно уметь брать сумму на отрезке и уметь каждый элемент отрезка заменять квадратным корнем из него, округленным вниз. Сумма всех элементов изначально не превосходит 1018
Я придумал решение за 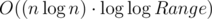 (
(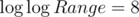 и я не уверен
и я не уверен 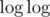 ли это). Идея тупая: каждое число станет единицей, если взять корень 7 раз. Тогда заведем 7 декартовых деревьев, первое из которых будет хранить текущий массив, второе — корни из его элементов, третье — корни из корней и так далее. при запросе на замену на корень вырежем из каждого нужный отрезок и сделаем циклический сдвиг вырезанных отрезков. Отрезок дерева, который мы вытащили из самого первого дерева зальем единичками (после этого вставим в последнее).
ли это). Идея тупая: каждое число станет единицей, если взять корень 7 раз. Тогда заведем 7 декартовых деревьев, первое из которых будет хранить текущий массив, второе — корни из его элементов, третье — корни из корней и так далее. при запросе на замену на корень вырежем из каждого нужный отрезок и сделаем циклический сдвиг вырезанных отрезков. Отрезок дерева, который мы вытащили из самого первого дерева зальем единичками (после этого вставим в последнее).
Такое решение дает ТЛ. Интересно, можно ли быстрее и/или проще?











Достаточно 6 раз извлечь корень
Ну, может быть. Я руками посчитал, видимо корявый.
Можно делать то же самое деревьями отрезков. Точно так же заведем восемь (+-1) деревьев отрезков. Заметим, что если у них одинаковая структура, то в каждом дереве при запросе на одном отрезке будут затрагиваться одни и те же вершины. Значит, можно будет произвести циклический сдвиг этих вершин. Это тоже log n * log log Max на запрос, но константа гораздо меньше.
Точно могу сказать, что таким способом делалась задача "Загадочное устройство" с (если не ошибаюсь, она с какого-то NEERC).
Клево, спасибо.
Это E с северного ЧФ 2009.
Я решил простым деревом отрезков. Как вы правильно подметили, количество раз которое можно из числа взять корень пока он перестанет меняться, ограничено (маленькой) константой. Поэтому количество раз которое нам придется действительно менять значение каждой вершины тоже ограничено этой константой. Достаточно пометить те вершины которые отвечают за отрезки где все элементы равны 1, и больше их не трогать.
можно ещё любой RSQ (Range Sum Query — фенфик например) + set, где храним позиции не единичных элементов.
О, круто, точно. Классное решение.
Nobody answered! Why??? :'(
I was doing the same problem and got stuck. -_-
Actually, two solutions were proposed. But in Russian.