Problem link: http://www.spoj.com/problems/PATULJCI/
Solution link: http://ideone.com/NqSI3j
Verdict: TLE
I tried to use Mo's algorithm and segment tree to solve the problem. How do I further optimize my solution? Any help is really appreciated.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Problem link: http://www.spoj.com/problems/PATULJCI/
Solution link: http://ideone.com/NqSI3j
Verdict: TLE
I tried to use Mo's algorithm and segment tree to solve the problem. How do I further optimize my solution? Any help is really appreciated.
| Название |
|---|



You need O((n + q) log n) to get AC, or something very close to that.
Try to only use one segment tree, that gives you any "dominant color" in an interval, for which you then check if it appears enough times in the interval. The solution is completely online.
How to use segment tree in this case?
Notice that in a node of the segtree, its dominating color, if there is one, has to be a doninating color of one or both of its children. Then, you can store in each node the dominating color. To merge nodes, you can query the number of each dominating color in both nodes, and see if they can be dominating in the new node. You can do this with order statistic tree or BIT and get O(log^2 n) time per query.
To get log n time, I think you can have your segtree store the 2 colors with most number of occurrences, and the number of times they occur. Now observe that a dominating color on the new interval has to be among the colors in the top 2 for each node, so you can check all of those colors using segtree values.
Oh, sorry! My bad :)
About the log n approach, I don't think storing the 2 colors that appear the most is enough. For example, every color on a segment may appear only once. But the general idea seems correct, thanks for the anawer.
Yea the number of times each one appears should also be stored
An alternate solution is by using persistent segment trees. At a node if we have two subtrees with sum of frequencies as S1 and S2, our answer either exists in the subtree with greater sum or doesn't exist. This gets AC in O((N + Q) * logN).
There is a solution with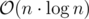 but I describe the
but I describe the 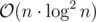 one.
one.
Let occ(x, L, R) as a function that returns the number of i's such that L ≤ i < R and ai = x. It's easy to implement, for each color like x, keep a vector of indexes that ai = x then answer is
lower_bound(vec[x].begin(), vec[x].end(), R) - lower_bound(vec[x].begin(), vec[x].end(), L).Now use segment tree. Consider a node for segment [L, R), keep the color that appears in [L, R) strictly more than (R - L) / 2 in that range, if there is no color satisfies the condition, save -1 there.
It's easy to merge two nodes:
Here is my code : Link.
This problem can also be solved with a randomised algorithm. You can see my solution here. The details can be found out in the editorial of this problem on codechef which is a harder version of the above problem with point updates as well.