2017 Facebook Hacker Cup Online Round 1

8 years ago, # |

+18

What is the memory limit in Hacker Cup?

→ Reply

bciobanu

8 years ago, # ^ |

+24

As long as it runs locally it's fine.

→ Reply

SangBijaksana

8 years ago, # |

+75

people : How's the contest going?

me :

→ Reply

8 years ago, # |

I am getting the links for the contest only from CF. Where are links written on the official page? I can't find it.

→ Reply

satyaki3794

8 years ago, # ^ |

This is the post for Round 1, on the official Facebook page.

→ Reply

mkirsche

8 years ago, # ^ |

They posted it here (along with the point cutoff) shortly before the round started: https://www.facebook.com/hackercup/posts/1384524328246418

→ Reply

duckladydinh

8 years ago, # |

Does anyone have any idea about file size or memory constraints? I need to use about 10^9 integers :v

→ Reply

8 years ago, # ^ |

It's okay to use it, if it runs locally.

→ Reply

redocyz

8 years ago, # ^ |

I believe it is fine just as long as you manage to produce the output file. (does not have to run locally. i.e, if you use a online compiler and such)

→ Reply

tfg

8 years ago, # |

Note to self: Always check if you swapped the output/source files.

→ Reply

Martial

8 years ago, # |

+63

Out of 5297 participants:

261 got a perfect score,
2418 got a score of 35 or above.

→ Reply

dario2994

8 years ago, # ^ |

How did you manage to get these numbers?

→ Reply

poikniok

8 years ago, # ^ |

+19

Probably by just clicking through the standings page, takes 5 minutes at most.

→ Reply

contest_dhuye_pani_khai

8 years ago, # ^ |

2 if you involve binary search (provided you have a fast net too) :v

→ Reply

iliekcomputers

8 years ago, # |

For A: Pie Progress, wouldn't O(N**2 * M) DP be too slow? I see that it is mentioned in editorial as a solution. Did anybody get it to run?

→ Reply

himanshujaju

8 years ago, # ^ |

Yes, in 2s it passed the input file.

→ Reply

mogers

8 years ago, # ^ |

I solved it that way as well.

N and M are only up to 300, so a cubic solution is perfectly fine.

→ Reply

Trem

8 years ago, # ^ |

-38

There is a O(N * M * log(N)) solution using divide and conquer DP optimization.

→ Reply

8 years ago, # ^ |

You can use winner tree data structure and it would take n*m*log(m)+n*log(n)

→ Reply

8 years ago, # ^ |

I managed to solve it greedily: solution.
I can explain if someone is interested.

→ Reply

trunghai95

8 years ago, # ^ |

N^2*M is too fast for 6 minutes.

→ Reply

mathlover

8 years ago, # |

+18

Poor network.... When I finish the coding of A, and click the "submit" button. It costs about 5minutes for downloading the input about 5 MB input. Fortunately, I run and upload as quickly as possibly. I suddenly realize why the problem C has a DP solutions with O(N^3+K) but K is only 5000, not 1e6.

→ Reply

8 years ago, # ^ |

I also have problem downloading the input files. Because Facebook is censored in Iran I have to use VPN and it slows down the network. It takes me minutes to download the input files.

→ Reply

mnbvmar

8 years ago, # |

← Rev. 2 →

+19

Now that the round has finished, what's your output to the following testcase? [Problem B]

Of course, it is 4.

Edit: saw the editorial, it's quite neat. However, I guess many contestants (including me) answer 3 on this test. :)

→ Reply

8 years ago, # ^ |

← Rev. 2 →

+21

I didn't really expect to get AC with this solution, but somehow I got it.

Solution

ll tests;
	cin >> tests;
	for (int ii = 1; ii <= tests; ii++)
	{
	 	cin >> n >> m;
	 	for (i = 0; i < n; i++)
			cin >> a[i].X >> a[i].Y;
		 ll ans = 0;
		 for (i = 0; i < n; i++)
			 for (j = 0; j < n; j++)
			 	for (k = 0; k < n; k++)
					for (l = 0; l < n; l++)
					{
						ll tmp = 0;
						for (r = 0; r < n; r++)
							if (a[r].X >= a[i].X && a[r].X <= a[i].X + m && a[r].Y >= a[j].Y && a[r].Y <= a[j].Y + m ||
							a[r].X >= a[k].X && a[r].X <= a[k].X + m && a[r].Y >= a[l].Y && a[r].Y <= a[l].Y + m)
								   tmp++;
						ans = max(ans, tmp);
					}
 		printf("Case #%d: %d\n", ii, ans);
	}

→ Reply

wjomlex

8 years ago, # ^ |

This is indeed the intended solution.

→ Reply

8 years ago, # ^ |

Yes, I already read the editorial and was surprised. With this solution the task becomes easier, than first.

→ Reply

8 years ago, # ^ |

And your solution passed?

→ Reply

mnbvmar

8 years ago, # ^ |

← Rev. 3 →

Well, no — I failed on a single test having n = 2. xD

However, quite a few of my friends passed, yet they get incorrect result on my test. All of these people stated that any feasible Move operation should be one of the following:

move a single point,
move a set of points inside a circle whose diameter is given by two points,
move a set of points inside a circle circumscribed on triangle given by three points.

However, the test proves this approach wrong.

→ Reply

8 years ago, # ^ |

It's OK, shit happens :)

Just curious, which of mentioned Move operations has your solution used? Let me guess — triples of points?

→ Reply

8 years ago, # ^ |

He meant that some people tried all of those rules in their solutions. But it's still wrong.

→ Reply

8 years ago, # ^ |

Thanks, understand now.

→ Reply

forest

8 years ago, # ^ |

← Rev. 3 →

This approach is not completely wrong, there is one more operation type to check:

move exactly 2 points (it can be checked by iterating through the third point, building a circle on 3 points and verifying a) no points lie strictly inside b) there are no points on upper circle arc OR there are no points on lower circle arc relative to the chord formed by the initial 2 points)

This passed in the round and returns correct result for your test

------ UPD: Well, I challenged myself with a slightly modified test case

Got 5 instead of 6

→ Reply

8 years ago, # ^ |

-10

You can only check for circle of infinite radius which is a half plane.

Take a look at this comment for proof.

→ Reply

8 years ago, # ^ |

+118

Will FBHC ever start creating good testcases :|? FBHC's quality of tests is pretty pathetic. In previous round, I am sure a lot of people will fail cases mentioned in topic about quals in first problem. Here in B many people including me did some stupid things like "create a circle passing through every triple of points" which can be done right, but it is very easy to get them wrong. And I expect many of passing solutions to that problem to actually fail on some cases. Mine fails case mentioned by mnbvmar, but there are other families of testcases which can be troublesome to many solutions. Model solution is great and contains no weird geometry with circles, and I know it is impossible to create perfect tests, but it looks like FBHC organizers do not even try to come up with any wrong solutions or think about mistakes that competitors can do which is essential in order to create good tests.

→ Reply

8 years ago, # ^ |

I thought about solution for triples and proved, that it's incorrect. So I sent O(n^5) brute with 2 squares, because I coudn't disprove it. I didn't really prove it.

→ Reply

8 years ago, # ^ |

And your "stupid things" passed?)

→ Reply

8 years ago, # ^ |

← Rev. 2 →

+31

Yeah, I did exactly what mnbvmar described and it fails on test provided by him, but it passes systests.

→ Reply

8 years ago, # ^ |

Wow. If so — congrats to you for bypassing it and shame on FBHC tests creators.

→ Reply

Zlobober

8 years ago, # ^ |

+27

Can't agree more. Looks like the most part (if not all) of the tests is generated by a pure random.

By the way, if even with current weak test cases of FHC many strong coders fail problems, just imagine how cruel system testing would be with strong enough tests. If I could participate in such a competition, I would be sooo happy, it could be much more interesting and funny.

→ Reply

Zlobober

8 years ago, # ^ |

+32

Hah, you think your solution is the worst that passes the full testset? Take a look at this.

Looks like they lack experienced problemsetters among round authors.

→ Reply

8 years ago, # ^ |

+23

Well I didn't get the intended solution. But I just decided to check all possible sets of points which one could bound in a circle. So it's either empty subset, some vertex, or we should choose two of them and look over all circles passing through these two and some other vertex. You can just look over a perpendicular bisector and sort all centers of these circles (and using scan-line get n+-eps circles). That's where I was afraid of EPS problems, so I made everything in ratios of (__int128/long long) (but was pretty sure that authors would forget about it). After that I have O(n^3) sets, and I check them in O(nlogn) by events on scan-line.

Well I'm really sad that something like you're describing passed systests with such small effort. I hope there will not be such a problem in the next rounds.

→ Reply

8 years ago, # ^ |

+13

You should've also checked circles of infinite radius.

→ Reply

8 years ago, # ^ |

+12

I don't need to check them.

→ Reply

8 years ago, # ^ |

Last time I didn't have enough time to prove that having two potion of second type is the same as having one of each.

You should've also checked circles of infinite radius. Which turns out to be enough and there is no need to check for other types of circles.

A circle of infinite radius turns out to be a half plane.

It's obvious that having two potion of second type is as good or better than having one of each.

And it's possible to cover any pair of squares only by transforming using a half plane(potion of first type can do this) and then using a potion of second type. (If area of the intersection is 0 it's obvious. And if intersection has positive area then primers of squares are either intersecting in infinite number of points which is obvious that we can transform this or they intersect in two points. Draw a line through two points and transforming one side of the line.)

We've showed that having one potion of each type is the same as having two of second type.

→ Reply

8 years ago, # ^ |

I didn't understand what you called "potion". I just told you that I had different solution. I'm not checking halfplanes (yes, it's enough, and it's the intended solution). I check all circles (and halfplanes are also checked by themselves as case of center lying far away from two points). You can read how to do it more precisely in the answer to Swistakk lower. Or read my code.

→ Reply

8 years ago, # ^ |

-13

Sorry it's my mistake. I used "potion" instead of "geometer".
Always wizards make potions but here in this problem they make geometers!

And yeah I see that now.
Nice trick! It can be useful in many problems.

→ Reply

8 years ago, # ^ |

Did you consider circles which almost contain some point? I mean, if we fix two points and consider event "in time T point P appears" then we need to create circles for times both T and T-eps (similarly with disappearing). You didn't mention it, but I guess you did it because I couldn't hack your solution.

→ Reply

8 years ago, # ^ |

I automatically checked it. So for example if you choose points (0,-1) and (0,1), centers are always on the line (c,0). Let's look at some other point (x,y). If x = 0 then it's doesn't matter what c you chose (you are always inside or outside). If x != 0 then let's denote the center of (0, 1), (0,-1) and (x,y) as (z, 0). if (x > 0) then you're inside the circle if c >= z (if x < 0 then you're inside if c <= z). So I start increasing c from -inf to inf, sometimes changing states of points (maximum once for one point). As always in scan-line algorithms you should fix the order in which you consider events with equal c (this will automatically at first check c and after that c + eps).

→ Reply

mugurelionut

8 years ago, # ^ |

+23

I also have the solution which tries circles passing through 2 or 3 points (or almost zero area circles containing just 1 point) — and, as mentioned, it passed the test cases I got (although there are counter examples to this approach). But what's worse is that it would have passed all the test cases even with trying just circles defined by any pair of points (I printed the results I got without considering triples of points and they were all the same for the official test cases I got). Of course, during local testing, I could easily find test cases where triples of points were producing better solutions than just pairs of points.

→ Reply

yeputons

8 years ago, # ^ |

+18

To those who don't understand that testcase (like me), here is a picture (source in Asymptote):

Red are points from the input, blue circle specifies the correct area for the "Move" spell, blue arrows are its direction, blue rectangle is the correct area for the "Destroy" spell. Note that only points 2 and 3 are moved and as a result they coincide with points 0 and 1, which could be covered by the rectangle.

However, if you assume that the circle is a circumcircle for some subset of points, you gonna have a bad time: magenta circle is a circumcircle for 2 and 3, but it also covers point 1. So, one should also consider circles of greater radius.

→ Reply

zholnin

8 years ago, # ^ |

My thinking process was (as apparently there was no limit on radius of circle) that I can actually approximate any line segment of length R (or longer) with the circle. Which is true in the limit. So I dropped that idea about circles (who does circle geometry in second problem in Round 1 anyway??) and just thought whether I can separate points I need to move by line. And it immediately leads to the idea that you should just look for two squares.

→ Reply

vovuh

8 years ago, # |

i wish to add the contest to gym. i can download inputs and solutions? if i can't, please, share it to me! thank you!

→ Reply

koderliar

8 years ago, # ^ |

RIP english, I assume you want the I/O files to make a gym contest, in that case you can find full I/O files here: https://www.dropbox.com/sh/bvnrwslazmr5ztc/AACZYKtzHq1mY4YrRQN-GFbDa?dl=0

→ Reply

vovuh

8 years ago, # ^ |

thank you a lot! i know that my english is worst, because i was learn german in the school. ;(

→ Reply

rajiv

8 years ago, # |

Hey! Where can we find the editorial for this.

→ Reply

sandoval95

8 years ago, # ^ |

Editorial link

→ Reply

kyuridenamida

8 years ago, # |

+82

It made me laugh that the test cases for the problem D included only R_i <= 50 although "Ri <= 20000" was written in the statement.

→ Reply

Xellos

8 years ago, # ^ |

Fail. My solution works in O(N·maxR) per test (or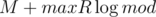 $\text{[math]}$ per test).

→ Reply

8 years ago, # |

I am reading editorial for the problem Manic Moving and I am thinking about the following sentence:

f(0, P, H) = the length of the shortest path from P to the N-1th family’s destination, and then to the N-2th’s family’s destination if H = 2.

Did they make a mistake with the visiting order? Maybe we should first go to N-2th family destination and only after that to the N-1 family?

→ Reply

mogers

8 years ago, # ^ |

Note that R = 0 here. So, there aren't any belongings left to deliver after this. Hence, to achieve this, we must have transported family N-1's belongings. If H=2, it means we also had family N-2's belongings loaded in the truck.

→ Reply

FunTry

8 years ago, # |

in problem "Manic Moving" ... if we have this "His truck is large enough to fit at most 2 families sets of belongings at a time" ==> "and fit at most "p" families ..." !

how can solve it? ... order?

→ Reply

8 years ago, # |

Is it correct implementation?

Manic Moving

#include <bits/stdc++.h>

using namespace std;

const int MX = 100, INF = 1e9;

int d[MX][MX], p[5001], q[5001];

int main() {
	int T;
	scanf("%d", &T);
	for (int t = 1; t <= T; t++) {
		int n, m, k;
		scanf("%d %d %d", &n, &m, &k);
		
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++)
				d[i][j] = INF;
			d[i][i] = 0;
		}
		
		for (int i = 0; i < m; i++) {
			int u, v, e;
			scanf("%d %d %d", &u, &v, &e);
			u--; v--;
			d[u][v] = d[v][u] = min(d[u][v], e);
		}
		
		for (int k = 0; k < n; k++)
			for (int i = 0; i < n; i++)
				for (int j = 0; j < n; j++)
					d[i][j] = min(d[i][k] + d[k][j], d[i][j]);
		
		for (int i = 0; i < k; i++) {
			scanf("%d %d", p + i, q + i);
			p[i]--;
			q[i]--;
		}
		
		long long A = 0, B = INF, v = 0;
		for (int i = 0; i < k; i++) {
			if (d[v][p[i]] == INF || d[p[i]][q[i]] == INF) {
				A = -1;
				break;
			}
			
			long long AA = A + d[v][p[i]];
			long long BB = B;
			
			A = min(BB + d[v][q[i]], AA + d[p[i]][q[i]]);
			B = min(BB + d[v][p[i + 1]], AA + d[p[i]][p[i + 1]]) + d[p[i + 1]][q[i]];
			
			v = q[i];
		}
		
		printf("Case #%d: %lld\n", t, A);
	}
	
	return 0;
}

I am particularly interested in the correctness of the following part:

A = min(BB + d[v][q[i]], AA + d[p[i]][q[i]]);
B = min(BB + d[v][p[i + 1]], AA + d[p[i]][p[i + 1]]) + d[p[i + 1]][q[i]];

It seems like this code doesn't handle the case when the optimal path for 3 families looks like that (s — starting vertex, f — finishing vertex):
s₁ ⟶ s₃ ⟶ f₁ ⟶ s₂ ⟶ f₂ ⟶ f₃.

But this code has passed all of the tests.

→ Reply

Alex_2oo8

8 years ago, # ^ |

+10

Quote from the statement:

However, Wilson has been instructed that the K families must be helped strictly in order. In particular, if i < j, then the ith family's belongings must be loaded before the jth family's belongings are loaded, and the ith family's belongings must be delivered before the jth family's belongings are delivered.

The $\text{[math]}$ part seems to violate this rule.

→ Reply