214A - Система уравнений
В данной задаче решение — просто перебрать возможные пары чисел и проверить их на правильность. Делать это можно было любым способом.
214B - Домашнее задание
Число делится на 2,3,5 только в том случае, если сумма цифр кратна 3, а последняя цифра 0, то есть если в наборе нету нулей, то ответ -1. Дальнейшее решение — разбор случаев.
Возьмем все цифры в невозрастающем порядке, если сумма цифр кратна 3, то это и есть ответ. Если остаток от деления вышел 1, то нужно убрать 1 цифру у которой остаток от деления на 3 равен 1. Если такой не нашли то нужно убрать 2 цифры с остатком 2. Аналогично рассматривается случай когда изначальный остаток равен 2. Так-же нужно рассмотреть случай когда остались только нули, в этом случае нужно вывести только 1 ноль.
213A - Игра
Решение — жадность. Пусть у нас компьютеры стоят по кругу, и ходами "вперед" назовем перемещения (1->2, 2->3, 3->1), а перемещением "назад" (1->3,3->2,2->1).
Заметим что ходить "назад" не выгодно, так как можно 2 раза походить "вперед", что в сумме равноценно. Будем перебирать стартовую вершину. Дальше будем ходить по кругу до тех пор, пока не "откроем" все уровни. В авторском решении для каждого уровня поддерживается количество уровней, которые нужны для него. После того как мы находим очередной 0 в этом списке, мы просто уменьшаем такую величину для всех уровней, которые от него непосредственно зависят. Сложность решения O(n^3).
213B - Числа
Решение — динамика. Перебираем длину числа, которое будем строить. Далее будем пользоваться динамикой f(len,i) — сколько чисел диной len можно составить из цифр i..9.
Пересчет:
- f(len,0) = sum(f(len-i,1)*C(len-1,i), i=a[0]..len);
- f(len,j) = sum(f(len-i,j+1)*C(len,i), i=a[j]..len), 0<j<9;
- f(len,9) = 1, если len>=a[9], 0 если len<a[9].
C(n,k) — количество способов выбрать k элементов из n.
213C - Эстафета
Решение — динамика.
Заметим, что мы можем просто провести два пути их клетки (1,1) в клетку (n,n).
Заметим, что после каждого шага клетки будут оставаться на одной диагонали. Будем решать задачу динамикой f(d,i1,i2), d — номер диагонали, i1 — 1я координата 1го маршрута, i2 — 1я координата 2го маршрута. Понятно что вторую координату мы можем определить однозначно. Переходы — очевидны, делаем 4 возможных перехода, если маршруты пересеклись, то добавляем величину клеточки один раз, иначе добавляем величины посещенных клеток. Так как данная динамика не влазит по памяти, то ее нужно делать двумерной, просто перенося значения из прошлой диагонали в новую.
Еще нужно не забыть про то, что ответ может выйти отрицательным.
213D - Звезды
Предоставлю разбор как небольшую презентацию картинками:
https://get.google.com/albumarchive/pwa/115317317397602031319/Solutions131
Реализация.
Единственную сложность могло составить определение координат, все координаты можно найти из правильного пятиугольника. Все что о нем нужно описано тут.
213E - Две перестановки
Первый шаг: заменить перестановки на обратные, то есть из перестановки A мы делаем перестановку B, такую что B[A[i]] = i. Если посмотреть на то, что получилось, то выходит такая задача: сколько подотрезков второй перестановки равны первой, в случае если мы "сожмем координаты", то есть числам сопоставим их номер в отсортированном виде. Эту задачу предполагалась решать хэшами, но брать их нужно было не только по основанию 2^64, а и еще по нескольким простым модулям, тайм лимит специально стоял 3 секунды.
Теперь, собственно, как ее решать: Для каждой позиции i — сопоставим коєфициент step[i], где step[i] = 1000003^i. Теперь Рассмотрим такую функцию: F(A) = num[1]*step[1] + num[2]*step[2] + num[3]*step[3] + ... + num[n]*step[n], где num[i] — порядковый номер элемента A[i] в отсортированном списке. Понято что эта функция однозначно задает множество, от нее и будем считать хэш.
Как пересчитывать при переходе не следующий элемент.
Заметим что когда мы убираем какой-то элемент, то все элементы которые больше его уменьшают значение num на единицу. Ровно как и после добавления они его увеличивают. То есть заведем Дерево отрезков/Фенвика для хранения таких величин как сумма степеней на отрезке и количество элементов на отрезку, что-бы за O(log(n)) находить величину num для числа и после каждого добавления/удаления будем пересчитывать хэш, тоже за O(log(n)). Так-же нужно будем умножать хэш на от первой перестановки на 1000003 после каждого смещения на 1 элемент вправо, так как коэффициенты step уже не будут идти от единицы.
Все замечания просьба писать в комментарии.
Через некоторое время постараюсь сделать формулы более красивыми.











D можно сильно проще: берем пятиугольник из семпла, сдвигаем его параллельно одной из диагоналей на одну, две и т.д. диагонали. Проводим длинную линию. дальше легко
Да, я уже это понял. Изначально не подумал о таком решении.
Еще можно было расположить на окружности но это не проще(
А тогда ответ вообще будет для n = 100, если ставить по окружности и без разворотов?
Я сдал в дорешивание. Да там с запасом хватает. На контесте я написал чтобы нижние основания были на окружности, но это конечно неправильно нужно чтобы диагонали были на окружности и ок.
У меня так же, как у тебя. Гораздо проще.
А почему в задаче Е нужно было брать не только по модулю 2^64? У меня в дорешивании прошло. Здесь же вообще непонятно, как строить контрпример сразу под все нечетные основания.
Для гарантии. Я понимаю что не понятно как перестановку завалить, именно по этому я дал эту задачу.
Вот генератор, валит все зашедшие на контесте решения, кроме моего. Правильный ответ (вроде) 21.
Респект Zlobober за идею, конечно.
Авторские ради предостережения были написаны по трем модулям, они тоже 21 выводят.
В div1 C динамика отлично влазит по памяти (по крайней мере в С++).
У некоторых не зашло.
А можно пожалуйста 213-B Числа подробнее объяснить? В частности что означает функция sum() и вот эту строку - f(len,9) = 1, если len>=a[9], 0 если len<a[9].
Спасибо.
функция sum() — прибавление f(len, i); f(len,9) = {0, 1}, потому что либо можно получить число состоящей только из 9, например f(2, 9) = 1, это значить что можно получить число 99, либо нельзя получить это число так как len < a[9], т.е не соответствует условиям задачи.
Подскажите пожалуйста как посмотреть полностью тест 16 из задачи B. Или какой хотя бы там смысл.
Никак :-(
Sereja , thanks for writing the editorial. Can you explain solution to 213C(Relay) more detailed? Using the English version translated by Google, I was confused.
It would be better if you submit your reference solutions with proper comments.
I would be appreciated if someone explains the idea behind Petr's solution to 213C, especially what the state best[][] means and how the transferring works, note that it's 2d(two dimensional) instead of 3d used by most contestants which reduced a lot of memory.
Most contestants use best[step][x1][x2], but you only need to know best[step-1][][] when you are calculating best[step][][], which means you don't need to store best[x] (x < step-1). So you can compress best[MAXSTEP][][] to best[2][][], or like Petr use best[][] best1[][].
in 213B f(len,i) is equal to the quantity of numbers we can build using digits i..9 of length len.but why do we multiple in formulas for example f(len-i,1)*C(len,i),should not it be f(len-i,j+1)*C(len,i),please tell me where's my mistake,thanks in advance
I think it should be j + 1 too.
Мне кажется, что в задаче D div2, во второй формуле должно быть: f(len,j)=sum(f(len-i,j+1)*C(len,i), i=a[j]..len), 0<j<9;
It would be nice to see a visualisation of some interesting solutions for stars (div1 D).
I think it's difficult for me and I cannot understand it yet...= =
This is another easy solution for problem D: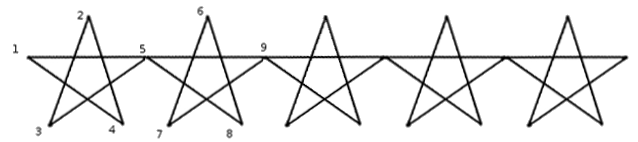
Assume that the distance between 2 vertices (1-5) is len. After pre-computing the positions of 4 vertices 1 2 3 4, positions of others vertices can be calculated easily by adding k * len to the x coordinate of the first 4 stars (for example, if we know (x3, y3), then (x7, y7) = (x3 + len, y3))
To draw the stars, for example, with n = 2, we can do like this: 1 5 9 7 6 8 5 3 2 4 1.
Nice solution.
In the example of problem E,why "1 3 5 2 4 1"is correct but "1 4 2 5 3 1"is wrong? I just output them in an opposite way.
Sorry ,it's problem D
I think the time complexicity for 213A is O(3*N^2)(N^2), not O(N^3)
Well, O(N^2) is a subset of O(N^3) :), but you're right, the time complexity of the algorithm described by Sereja is O(N^2).
It will work O(n^2) only if we will find all zeros(when there is not any edge to the vertex) quickly. Of course it is easy. But my solution works O(N^3) at worst case.
It is A problem, so I think that it is normal, when such solution can passed system tests.
Are you sure that it's O(N^3)? When we go around 3 computers, we'll always find at least one zero, so we'll perform O(N) loops. Since you maintain a degree array (and I'm very sure that you also use a boolean array of visited vertices), it's possible to find a zero in O(N). And for each zero you decrease O(N) items in the degrees array. The result is O(N) * (O(N) + O(N)) = O(N^2). What have I missed?
Yes, you are right :)
Насколько я понял, в разборе к задаче 213B, тут:
- f(len,j) = sum( f(len-i,1)*C(len,i), i=a[j]..len ), 0<j<9;опечатка.Вместо,
f(len-i,1)нужно использоватьf(len-i,j+1). По крайней мере, у меня так ( кстати, еще есть пару опечаток ) прошло.In problem 213E,I have a question. when you use hash,why do you choose 1000003,and it is likely that F(A) you define exceeds long long? What should you do to avoid the problem.
1). I use 1000003, becouse it's bigger then 200000 and prime. 2). I use long long's overflow (it's the same as get number modulo 2^64), but I also use hashes by some other modulos.
Does it possible that the hash crashes,that is to say,two different permutations have the same number modulo 2^64 ? But I notice that most people don't consider it.
Yes, it can be.
So I get an AC, But how should we improve it?
We can calculate hashes by modulos 1000000007 and 1000000009 instead of 2^64.
Can you assure that it doesn't crash if you use 1000000007 and 1000000009 as modulos. Also we can't store the permutations who crash.
We can't assume that. Hashes give big probability, but not 100%.
Ok,Thank you,I get an AC using 1000000007 as the modulo a moment ago,
Подскажите, пожалуйста по задаче C — эстафета. Работает ли такой алгоритм: с помощью простого ДП находим max путь из точки (1;1) в точку (n;n), затем с помощью поиска в глубину проходим по max маршруту обнуляя клетки, которые посетили. Потом простой динамикой ищем max маршрут из (n;n) в (1;1). И суммируем результаты маршрутов. Простая динамика: pole[i][j]+=max(pole[i-1][j],pole[i][j-1]); pole2[i][j]+=max(pole2[i+1][j],pole2[i][j+1]). pole2 — это матрица после прохода по 1-ому маршруту ( после обнуления ). Результатом я считаю pole[n][n]+pole2[1][1] Если алгоритм невереный, то почему? Ecли алгоритм работает, то где у меня ошибка 2087919?
Видимо, контрпримером против такого алгоритма может быть
Первоначально оптимальный путь — идущий всю дорогу по значениям 99. Но потом второй персонаж вынужден идти через 98, 11, 98. Тогда как можно сформировать 1-й путь как вправо, вправо, вниз, вниз, а 2-й как влево, вверх, влево, вверх, и так сумма будет больше.
In div2 B-Hometask, after ensuring there is a 0 in the list, I tried to find the maximum digits I can keep which will give me a sum % 3 == 0 using Knapsack DP. Here is my code Code. I got WA on test case 13. All I want to know, did I get WA due to stack overflow? Or is it not possible to find which digits to keep using Knapsack dp? Also, if stack overflow occurs in codeforces, do we get WA or run-time error?
I can't understand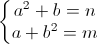 So it means:
So it means:
(a-b)(a+b-1)=n-mif n==m, a=b is a true answer that consists of infinite pairs. What is wrong with my insight? (problem A)not every solution of (a - b)(a + b - 1) = n - m is the solution of this system. Futhermore, the number of solutions of the system is finite, because if a > n or b > n then a2 + b > n
Can someone please explain in detail(in English) the editorial for div1 B?
Начал в архиве решать эту задачу и по сокращенным фамилиям героев понял, кто автор :)
comment deleted
Can someone give a proper explanation for 213C Relay Race . What does the author mean by "There are 2 paths from (1,1) to (n,n)" and also "after each move our cells will be located on the same diagonal."
Consider Rubik also starts from (1,1) and moves to (n,n) . (this will not change answer ) .
The diagonals refer these --.
Clearly at each step both will be on same diagonal
Knowing the diagonal number , and x-coordinate , you can get y = d-x + 1.
So , we store only diagonal number and x-coordinates for both rubik and furik
33898588