→ Pay attention
Before contest
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
23:53:15
Register now »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
23:53:15
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/22/2024 17:41:45 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Regarding tuples problem.
Suppose that for each y between 0 and m - 1 = 359998 you know number of Yi, j that are equal to y, let's call this value cy. In order to calculate the number of coprime triples, let's calculate for each g the number of triples that have gcd exactly g, call this value D[g]. We will calculate it using DP.
First of all, D[0] = c03. Now we will calculate the rest of D-values in order from higher values to lower. Triples having gcd exactly g are exactly those triples that have gcd divisible by g, but not equal to 0, 2g, 3g, ... Triple gcd is divisible by g iff all three numbers are divisible by g, so we have the formula: D[g] = (c0 + cg + c2g + ...)3 - D[0] - D[2g] - D[3g] - ...; For a fixed g this formula contains about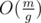 terms, so overall the complexity of this DP is
terms, so overall the complexity of this DP is 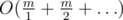 =
= 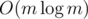 . That was the second part, the standard inclusion-exclusion-like DP.
. That was the second part, the standard inclusion-exclusion-like DP.
Now how to find out all cy. First of all, let's calculate cy for all y that are coprime with m = 359999 = 360000 - 1 = 6002 - 1 = (600 - 1)(600 + 1) = 599·601. Notice that 599 and 601 are both primes, so there is a bijection between all xi coprime with m and pairs (ui, vi) where 1 ≤ ui < 599 and 1 ≤ vi < 601 defined by the map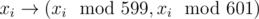 , the reverse mapping can be done via Chinese remainder theorem. Notice that this map is also multiplicative, i. e.
, the reverse mapping can be done via Chinese remainder theorem. Notice that this map is also multiplicative, i. e. 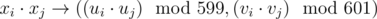 . Now let's make an additional step: we know that for
. Now let's make an additional step: we know that for 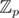 for prime p there exists a primitive root whose powers generate all elements that are non-zero in
for prime p there exists a primitive root whose powers generate all elements that are non-zero in 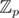 . This allows us to consider mapping
. This allows us to consider mapping 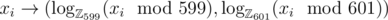 . Let's calculate for each xi the corresponding pair (ai, bi) by the formula above. This mapping transforms the product xi·xj to the sum of pairs
. Let's calculate for each xi the corresponding pair (ai, bi) by the formula above. This mapping transforms the product xi·xj to the sum of pairs 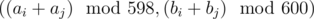 .
.
Now we need to calculate for each (c, d) how many times it appears in multiset consisting of all pairs written above over all i, j. This can be seen as a circular 2d convolution problem that can be reduced to FFT (details are left as an exercise and as a mercy for this comment that is already way too long to be read by somebody :D ).
In such manner we can find all cy that correspond to y coprime to m, the remaining y's can be dealt pretty similarly.
Very nice problem that requires to perform several steps in the solution, kudos to the author!
Can your briefly explain the last step i.e. while mapping the product to sum of pairs, why does the modulo values changes, 599 to 598 and 601 to 600. Also, how are the ci values not coprime with m dealt?
7 is primitive root modulo both 599 and 601.
Define discrete logarithm of as such number that
as such number that 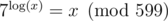 . According to the Fermat's little theorem,
. According to the Fermat's little theorem, 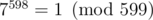 , so discrete logarithm is defined up to adding/subtracting numbers divisible by 598, i. e. discrete logarithming defines an isomorphism between
, so discrete logarithm is defined up to adding/subtracting numbers divisible by 598, i. e. discrete logarithming defines an isomorphism between 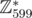 and
and 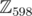 ; logarithm of a residual modulo 599 is a residual modulo 598 satisfying the property that logarithm of product is a sum of logarithms.
; logarithm of a residual modulo 599 is a residual modulo 598 satisfying the property that logarithm of product is a sum of logarithms.
Try to think about values cy for y not coprime with m by yourself. Consider three options: y is divisible by 599 but not by 601, y is divisible by 601 but not 599 and y is divisible by both 599 and 601 (that is equivalent to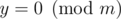 ). It involves several pretty simple but technical procedures similar to what we did above, I do not want to explain them in this comment. You may look into my code submission, are they available on Codechef now?
). It involves several pretty simple but technical procedures similar to what we did above, I do not want to explain them in this comment. You may look into my code submission, are they available on Codechef now?
I map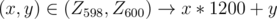 .
.
I did the same thing, this reduces the 2d-convolution to usual polynomial multiplication.
Approach to DIGITSEP please ! no editorial till now
Let dp(i,j) be the set of all elements we can obtain by applying j separators to all digits indexed 1...i. One fact that you can derive is that there will be very few distinct possible values for each dp(i,j), hence you can store all such values in a set to avoid repetition. Now, you can evaluate the set dp(i,j) by taking the last element to be of length k where k<=i, and applying the leftover j-1 separators to the leftover string.
I used a different state representation Let dp(l,rem,end) be the maximum gcd obtainable by placing separator at lth position with rem separators remaining and end means if I should terminate the sequence here . then ans will be dp(0,y,0) but I was getting WA my solution . Please see my solution (I have heavily commented it, It wouldn't take long) or give me some test cases in which my code fails.
The reason you are getting WA is because in the line no. 50 of your code for the gcd function it's not necessary that taking the maximum number always gives the best answer. Think of an example and you will get your mistake. Let us take an example for 3 variables a,b,c where a is 2 and b is 2 and c is 3 so selecting max(b,c)=3 and gcd(a,max(b,c))=1 but the max value of gcd possible is 2.
Could anyone explain their approach to the SEABOX problem? No editorial yet.
Okay, So this problem essentially requires you to solve the two different kinds of problems.
Finding the maxm: - Observe that if we have a 2 × 2 × 2 cube which is uniform,that is, it contains only 1's or only 0's, changing one of it's element will increase the answer from 1 to 8. Similarly if we have a 4 × 4 × 4 uniform cube, if we change only one of it's elements, the answer would change from 1 to 15. For 8 × 8 × 8 uniform cube, the answer will change to 22 .. and so on.
So, we can first count the number of uniform cubes of size {2, 4, 8, 16, 32} and greedily select the largest one to make it non-uniform and then the second largest one and so on... and find the maximum change.
Finding the minm: - This reduces to standard dynamic programming problem. For any cube, we have 2 choices, either make it all uniform or try to reduce it's 8 sub-cubes. If you want I can explain the DP.
Could you explain the dp relation once?