Hi guys ! Please explain this problemproblem with its solution . Thanks in advance !!
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
24:06:43
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
24:06:43
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 17:28:18 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










You have an NxN grid with M elements scattered around inside of it, you're asked to move the least number of elements such that each cell in the grid have at most one element and all the elements are arranged in a way such that they form a rectangle
Solution:
First: what are the dimensions of said rectangle?
We can see that they are the divisors of M which are at most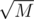 pairs, don't forget swapping width and hight
pairs, don't forget swapping width and hight
Second: which elements to move?
If we were to assume that our rectangle will occupy some arbitrary rectangle inside the grid, then the number of moves needed to rearrange the elements such that they would occupy that area is equal to E where E is number of empty squares in the rectangle
Third: which rectangle to pick?
The constrains are good enough for us to brute force all of them
We will do partial sums over 2D array of elements where grid[x][y] contains sum of empty squares in the rectangle designated by (1, 1)&(x, y)
With partial sums we can find number of empty squares anywhere in O(1) time
We have about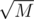 rectangles, let's try every possible top-left point for each of them, no more than N2 points in worst case
rectangles, let's try every possible top-left point for each of them, no more than N2 points in worst case
So our solution will run in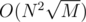 time
time
First lets change the statement, you are given the dimension (x,y) of the required rectangle (x * y = M). To solve this problem you can put the upper left corner of the rectangle in every cell of the given matrix and check how many cubes are inside of it. Suppose there are C cubes, then obviously the answer is M - C for this rectangle. Be careful with towers of cubes.
Having solved this problem, you can try all possible rectangles with dimensions (x,y) such that x * y = M and keep the one that requires the least amount of moves.
Thanks for this much clear explanation .