Вам дана последовательность A1, A2, ... , An, - 1000 ≤ Ai ≤ 1000, 1 ≤ n ≤ 1000.
Вы можете разделить ее на подряд идущие непустые подотрезки и от каждого оставить только его сумму
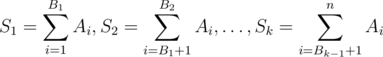 .
.
Необходимо максимизировать сумму произведений соседних подотрезков 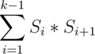 . Если k = 1 , то сумма равна 0.
. Если k = 1 , то сумма равна 0.
Может кто-нибудь дать хотя бы подсказку на правильное решение?











решение за куб:
dp[i][j] = max(dp[k][i-1] + sum(k..i-1)*sum(i..j))
тогда решение за n^2 можно получить, перебирая i и для каждого i сделать конвекс хул трик,
добавив прямые sum(k..i-1) * x + dp[k][i-1],
тогда перебираем j и сделаем запрос к нашей выпуклой оболочке с x = sum(i..j)
тогда dp[i][j] как раз будет максимум по dp[k][i-1] + sum(k..i-1)*sum(i..j)
Let dp[n][len] be the maximum value I can get with the first n elements of the sequence if the length of the last block is len. It is easy to see the formula dp[n][len] = mink(dp[n - len][k] + (sn - sn - len) × (sn - len - sn - len - k) where si is the accumulative sum of the first i elements. Now dp[n][k] = mink(dp[n - len][k] + (sn - sn - len)sn - len - (sn - sn - len)sn - len - k dp[n][k] = mink(dp[n - len][k] - (sn - sn - len)sn - len - k)) + (sn - sn - len)sn - len the first part can be calculated using convex hull trick, the complexity will be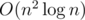
Btw is there a link to submit the problem??
http://mirror.codeforces.com/gym/101237/problem/F
In your question it is not clear whether you are given k or not. If you are not given k the solution provided by jcg will be correct. If you are given k the problem can be solved using the approach described here and here in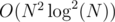 . But it can be further optimised to
. But it can be further optimised to 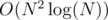 , because we can do convex hull (which we actually use inside the binary search) in O(1) time using a stack.
, because we can do convex hull (which we actually use inside the binary search) in O(1) time using a stack.
It seems that I reply to the correct statement.. In your version how you deal with the queries in the convex hull in O(1)? The values in the original sequence can be negative.