Here's the git repository containing source codes for problems of this contest.

Tutorial is loading...

Tutorial is loading...

Tutorial is loading...

Tutorial is loading...

Tutorial is loading...

Tutorial is loading...

Tutorial is loading...

Don't hesitate to ask if you have any question/suggestion.
UPD: Git repo was not completely public, it is now. You can clone it or you can browse codes in "Repository" section.











I guess it wasn't supposed that Ford-Bellman would pass Div. 1 B :D
My last minute submission: http://mirror.codeforces.com/contest/786/submission/25751732
I still don't understand why Bellman-Ford (or some sort of SSSP) doesn't work. Can someone explain why a segment tree is required? Is it not enough to construct a graph such that the edge weights are minimum of the costs required to open a portal. (We can check type 1, 2, 3 and see which gives us minimum edge between any two vertices u-v). I submitted 4-5 times but always failed a pretest (although most of the outputs seem correct). I understand my approach was wrong, but is there a simple test case which requires seg-tree?
Your code won't work at least for the reason you have g[i][j] vector, which is of size 105 * 105 = 1010 :D Just remember that arrays of size ≥ 108 or any number of operations ≥ 5 * 108 is too much
nice Div2C problem
The title of 6 tasks coincide with the names of Eminems songs, a coincidence?
For problem Div.2 A
Could anyone help me to prove this. It is not very clear to me.
Application of Euclid's Theorem.
See this link for detailed explanation Intersection of two APs
This problem also troubled me a lot.
I finally solved it together with my friend.
Suppose there exists a solution(i,j) which satisfies i * a + b = j * c + d.
Obviously,(i + kc, j + ka) is also a solution.
We need to prove the fact that there exists a natural number k which satisfies 0 ≤ i + kc ≤ N && 0 ≤ j + ka ≤ N.
We can deform the inequalities as -i ≤ kc ≤ N-i && -j ≤ ka ≤ N-j K∈N
∵ c ≤ N && a ≤ N ∴ kc exists in any interval whose length is N.
Similarly, we can prove that ka exists in any interval whose length is N.
The git repository isn't accessible
Sorry, fixed
Looks like nothing is in the repository
Thanks, but it seems there's still a problem :p no codes are there
Sorry to bother you.But I can't find any code in that git.
Is this a joke?
Why don't you do it the way Errichto did here? =)
The fastest Editorial !!!
For Div.2 C, Can someone tell me what the initial values for all my nodes would be?
Final vertex would have "lose state", anything else would be undefined
can you explain the logic of marking final vertex as lost? i mean why not to mark it as won? when player moves the monster into black hole he wins, so why we should mark as lost
But then how to recognise a loop state ? I was stuck in an infinite loop because I couldn't recognise the loop state.
I had the opposite problem. I was getting into infinite loops, recognizing them, and marking nodes as "loop". I couldn't get pretest #2 to pass, because I marked some nodes as "loop" prematurely. If I don't do that, I'm at infinite loop. I'm guessing the order in which you process nodes is very important. I don't understand why the editorial doesn't talk about that. You can not actually solve this with the solution given in the editorial.
you can use bfs in this problem.(of course on the reverse graph) and you should have a cnt for every node in the graph that shows how many neighbors of this node is in win state. first add the black hole nodes to the bfs queue and color them as lose. then for every node in the queue(named cur) if it is colored in lose then for every neighbor in the reverse graph(bigraph with all the edges reversed) color them as win.but if cur was colored in win then for every neighbor you should add 1 to cnt of this node.if at any point cnt of someone equals the number of its edges you should color it as lose and add it to queue. at the end if a node was colored (in lose or win) print as it is colored else print loop. here is my code for more information. hope i could help sorry for bad english
Isn't this 2*7000^2 operations? We process every node and from each node there may be 7000 edges to other nodes. edit: Ah, it's not that heavy because we can stop after we have marked all 2*7000 states as solved!
In Div1-C, how can we "use this segment tree to find the first r for an arbitrary k"?
Actually I wonder that too, have you found a solution after 6 years?
I solved Div.1 C with divide and conquer. First note that as k becomes greater, the answer will be less than or equal to previous answers. And for a fixed k, we can find the answer with binary search. So we can apply divide and conquer: 25753574
I failed to prove that this works in time, but it was accepted.
EDIT: With a little optimization(solve lower part(<=300) naively, and divide&conquer upper part(>300) using ans[300]) it runs faster. 25754474
For a fixed k, we can also find the answer naively without binary search?
Oh you are right! I missed that point. Without binary search, much easier to code and fast.
25762803
Can you explain the worst case complexity for this?
I suspect it's O(n log n) or O(n log^2 n), but I couldn't prove it: the worst case complexity is T(n, n) such that T(x, 1) = theta(x), T(x, k) = theta(n) + max(T(x / 2, i) + T(x / 2, k — i + 1)) for 1 <= i <= min(n / x, k). I have no further ideas.
Can you please briefly explain what is the general idea of your solution? Can't fully understand the logic of your code(
My first idea is from divide-and-conquer trick(DP optimization). It turns out that in my solution divide-and-conquer does not work well, but fortunately it did work in a different way than I expected. There can be only O(sqrt n) distinct solutions, and once you got ans[l] = ans[r] = x, ans[i] will be x for every l <= i <= r. My divide_and_conquer function "binary searches" the intervals of same answer.
I think it's of order O(N * sqrt(N)), because naive() is used for every distinct answer. Function f(k) = [N / K] takes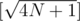 distinct values for strictly positive integer K.
distinct values for strictly positive integer K.
I think you're right. I just tested with n = 100000. naive function is called about 1500~1600 times with both random data and data of distinct integers (dat[i] = i).
Overall complexity might be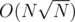 but
but 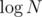 times.
times.
naive()function may be called multiple times for even same answer. Consider all distinct values i.e. dat[i]=i. For N/2, 3N/4, 7N/8,...naive()will be called and the answer will be 2 each time. So for answer as 2,naive()will be calledSimilar solution — but even more faster (notice this is Java). Idea is to cancel recursion and mark all values between low and high if low and high are the same. 25741766
an appropriate name for this contest should be "Lose Yourself"!
Can someone explain B Div1 in a clearer way?
First time 0 solved, I love your contests <3
But seriously
I will never attempt to submit again if I am 1h15' late.
I will never attempt to submit again if I am 1h15' late.
I will never attempt to submit again if I am 1h15' late.
:v
int i=3; while(i--) cout<<"I will never attempt to submit again if I am 1h15' late.\n";
Why in div2C / div1A we should mark position on black hole as lost?
Because if we assume that if the monster is already in a black hole, the current player can't move anymore. Therefore he loses
In D1A, how are we deciding which node to chose to update next. If we arbitrarily chose some node, recursive calls may lead to a call back on this node, hence giving an infinite loop.
25756312 check my submission. we only update things when we are sure we got their correct value.
Thank you, I tried looking at other codes but this one explains it well with all the comments.
Your effort stands out from other rounds! Awesome job!
In problem B I have a solution, which works in O(n * log(n))
http://mirror.codeforces.com/contest/786/submission/25744686
Div 1B solvable in single log complexity:
Use segment tree to record d for each position; additionally, keep track of the minimum d in a segment that is not yet visited.
Use interval tree to store all edges (keys are interval of start positions)
Now, modify "for each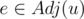 " step in Dijkstra's algorithm to
" step in Dijkstra's algorithm to
let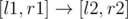 be any edge s.t.
be any edge s.t. 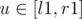 ; delete edge
; delete edge 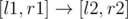 (!)
(!)
Greedy property of shortest path problem guarantees the deletion to be correct. Therefore total complexity is O(VlogV + ElogE) = O(ElogE).
This also works fine on generalized, interval-to-interval edges.
Could you please explain how segtree works with this problem? I don't quite realise what each node of the tree represents.
What do you do when you run a normal Dijkstra algorithm? You push the nodes in the priority queue. Every time you pop an unvisited as-of-yet node from the priority queue with the least distance, mark it as visited and consider all its neighbours. If for some neighbour, the new distance you get is smaller than the current distance to it, you update its distance and push it into the priority queue.
In this problem, you use a segment tree to replace the priority queue. Then you can update distances to the neighbours using a point update (for type-1 edges) or a range update (for type-2 edges). For the type-3 edges, you need to observe the fact that you will consider them only once, i.e. when you mark a vertex in its range as visited for the first time. That is because, for all other unvisited vertices in that range, their shortest-distance from source will never be less than this vertex.
Code
tree[] is the equivalent of the priority queue.
tree2[] returns any of the remaining type-3 edges which contain a particular vertex v in its range.
You can ignore the BIT. It is not used anywhere in the code. :)
This is crucial. Thanks for the hint.
Git Repository ain't working
Please help me :( I can't find out why my code was wrong: My code
you break the "while(k--)" loop as soon as you find the complement of a value x. suppose you have an input like:
4 2
1 1 -1 3
4 1 3 2 -3
when you stop the loop at "-1" and read k = 3 so you will try the next 3 values 4 1 3 :)
your solution has totally broken logic
at least you didn't take into account that one user can be in many groups many times
memory limit is so strictly !!!
Thanks, you have nice problems + cute pictures = solid contest!
I managed to solve Div1 C using some kind of sqrt decomposition. Link to submission: http://mirror.codeforces.com/contest/786/submission/25756668
Solve using the greedy algorithm for the first sqrt(n) answers. For the rest of the answers, keep the intervals that you use and the frequency of each color inside it. From one step to the other you need to stretch the intervals as far as possible. There are at most sqrt(n) intervals and each has 2 pointers: the left bound and the right bound. Each bound can go from 1 to n (they always go right) so the complexity of this part is O(n*sqrt(n)).
nice approach :)
tfg please help!
Could you prove why the second part of the algorithm has N*sqrtN complexity?
There are N-sqrtN values of 'k' left to be processed, and for each 'k' the left and right pointers might update O(n) times, making the complexity N*N. This is because the l[x] and r[x] pointers increment by steps of 1.
How can we say that l[x] and r[x] pointers update total of only N*sqrtN times over all 'k' that are to be processed after solve() ?
edit — I was able to prove it.
PrinceOfPersia
I solved problem C using only a binary indexed tree
But I solved all the queries together starting from the first element , taking the rightmost valid position for each query , and then pushing it on the next position (after the rightmost) to continue afterwards.
Of course maintaining the number of distinct elements from every start to every other position (a trivial problem) when i finish a position i remove the element and increment the next occurrence in BIT
my code is very clear
code
I was surprised that this problem was div1C :D
I've got a little bit easier approach that doesn't require persistent data structures. We can find the answer for each k simultaneously going from the beginning of the array a to its end and finding k-th minimum (using treap) for each k which has an end of a block at corresponding position. Details can be found in the solution: 25756864
Can someone please post a good explanation of DIV2 C.
You can think of it this way. Positions are characterized as winning or losing positions. If, from a state, you can send the opponent to a losing state, then you will ALWAYS make that move and the current state is winning. On the other hand, if all moves from the current state lead to a winning state for the opponent, you can NEVER win because no matter what you do, the opponent will win. So, the current state is a losing state for you.
This is exactly what has been used. The black hole is a losing state for the current player. There are 2n states in this game, (player, index) indicates that the monster is at 'index' location and it is the turn of 'player' (0<=player<=1).
In the BFS, if the current node is a losing state, then for all adjacent nodes which are unvisited, mark them as winning for the opponent.
If the current node is winning for the current player, just increment some count (which you're maintaining for each node) for its adjacent nodes. If for any neighbour, count becomes equal to the number of allowed moves from that state, that means EVERY move from that neighbour leads to a winning state. Hence, that neighbour is a losing state.
Now what remains are the unvisited vertices from the BFS. They are part of an infinite game. You can think of it this way. Suppose an unvisited state S has X neighbours. Out of them, some Y (Y<X) are winning. None of S's neighbours can be losing (because then S would be winning, not unvisited). Similarly, Y<X (because if Y==X then S is losing). In each move, you move the monster from an unvisited node to another unvisited node and this goes on and on. :)
This comment should be the editorial :)
what does "deg" stand for? i see this naming in many submissions of this problem
Vertex degree?
Yes, vertex degree.
can you explain how does this count help in finding losing state ?
If every node that you can reach from a node v (using some set of moves S) is a winning node, then v is a losing node (with respect to the set S).
WOW! Thanks a lot man for the insanely simple solution and proof.
Div 2 A was harder than I expected. I tried to solve the equation exactly and couldn't then I just said screw it I will just try all values of i and j from 1 to 1000 and if I haven't found an answer by I will assume that exist and it worked. It is nice to read that this reasoning was actually correct.
I have tried different k values from 0 to 108: time = b + k·a.
Now try to find m ≥ 0 such that time = d + m·c.
This solution is very easy to come up with and understand its correctness. No need for gcd's and lcm's :)
Problem set is good!
I solved Div1. C with an sqrt decomposition.
When K is smaller than , we can do an O(N) brute force to get the answer. We need to do this for
, we can do an O(N) brute force to get the answer. We need to do this for  times with each time O(N), so the total complexity is
times with each time O(N), so the total complexity is  .
.
When K gets bigger than , we can find that the answer is at most N / K. We maintain the squads when solving each K. When K changes to K + 1, we just need to check how many elements of the next squad (or maybe the next squad of the next squad, etc.) can be added into the previous one for each squad, and update it. The answer changes at most
, we can find that the answer is at most N / K. We maintain the squads when solving each K. When K changes to K + 1, we just need to check how many elements of the next squad (or maybe the next squad of the next squad, etc.) can be added into the previous one for each squad, and update it. The answer changes at most  times here, so each element will be added to a new squad at most
times here, so each element will be added to a new squad at most  times. And each time we just need to check
times. And each time we just need to check  squads, so the total time complexity is also
squads, so the total time complexity is also  .
.
Check my code for details 25762112 :D
thanks for sharing~ seems sqrt algorithm can be used to solve many data-structure problems? and easier
Your code is too obfuscated >.< !!!!!
Hard to read even with
g++ -E:|nice approach =)) tks u <3
Very nice problem set! One of the best problem sets that I have ever met.
Although I wasn't able to solve a single problem in the contest... but I still thank you for high-quality problems and nice editorials.
can someone plz explain what's actually is to be done in DIV 1 A??
Can I say mmp!?
What is the error in my code ,showing WA on a pretest. My submission: http://mirror.codeforces.com/contest/787/submission/25749836
Remove the
breakhere, since you haven't finished reading the input in that line.For div 2 A how to prove "if a, b, c, d ≤ N, and such i and j exist, then i, j ≤ N" ?
We have to solve a Diophantine equation: b + ia = d + jc, with a, b, c, d ≤ N.
This is equivalent to ai + ( - c)j = d - b.
If this equation has a solution (i0, j0), with i0, j0 > N, then we can construct all other solutions, like so:
Now, given this way of construction and that ,
, 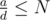 , we see that we can keep reducing the values i0 and j0, until at least one of them is between 1 and N.
, we see that we can keep reducing the values i0 and j0, until at least one of them is between 1 and N.
Thus, in our algorithm, if suffices, to inspect values i and j such that 1 ≤ i, j ≤ N. This yields a complexity of O(N).
This is the most rigorous proof I could come up with while refreshing some number theory concepts I had forgotten about, but in a contest environment you probably don't need this kind of thinking, as you can just rely on your instinct and simply plug in value i within some big constraints, like 1 ≤ i ≤ 106. This, I suspect, works just fine.
For Div1 A — Berzerk, why is this property true:
If a state has an edge to a lost state, it's won? Can someone provide an intuition/proof for it?If the first player loses then the other player MUST win. That is, in order for player2 to win, player1 has to lose.
There is another simple solution for div.1 C. Let's take some answer and define r[i,j] — rightmost point of j-th block where k=i. Obviously that r[i,j]<=r[i+1,j]. j-th block where k=i cover segment r[i,j-1]+1...r[i,j]. Let's build optimal answer by adding 1-st block for every k, then 2-nd, then 3-rd and so on. Let's imagine we calculated r[i,j] for i=1...n, j=1...x. How to calculate for j=x+1? Let's greedy get x+1 block for k=1. Okay. It's easy. Let's maintain cnt[val] — count of occurancies of val on our current segment. When we move our segment we can maintain count of different values on it. Okay. We get r[1,x+1], how to get r[2,x+1]? For k=x+1 we have needed data for segment r[1,x]+1..r[1,x+1]. Let's define bounds of current segment as L and R. We know that L>r[2,x+1], so we just move leftmost bound of our segment right until inequality is not satisfied. Now when we moved our segment left bound right as far as we can, we can move rightmost bound also. Just. Do it. Move R right until the end of array or next element will mage our segment "bad"(too many different elements). And so on for i=3...n.
Link : 25759518
I am not sure in time complexity of the solution so will be grateful if someone help me with it.
In Div 2B, what is CNF formula and how to solve it. And how the complexity suppose to be O(n+m). I'm able to solve it only in O(m*n)
If there are 2 opposite numbers in a group (for example, 3 and - 3), then this group cannot be a bad group. Otherwise, that group can be bad.
I get that. But I'm not able to get that how it's gonna solve in O(m+n) instead of O(m*n) complexity.
I see. I think that he has put a plus sign instead of multiplication because of the statement: "Sum of k for all groups does not exceed 104". In general case, your estimate of O(n·m) is better.
Actually i think the complexity can be optimised by using that CNF equation, which he is using in tutorial. Do someone know about that CNF formula.
You are wrong. The complexity cannot be less than the input size :)
Oh ya that thing I didn't consider mistakenly. So now the complexity is O(m*n). But can you suggest some reading material or something on that CNF equation. It might not be needed in this question but who knows I can use that in some other question.
Usually, these types of problems are about 2-CNF and they start appearing from Div2D. It is pretty difficult to understand how to solve them. I don't think it is a good investment of your time.
That being said, here is an article 2-SAT :)
Can someone explain div 2 D editorial clearly ?
PrinceOfPersia please explain how to handle 3rd type query. Nvm, figured it :)
I want to ask a question about Div2D / Div1B Legacy
Code
My accepted solution is build 2 different segment trees which connect vertex on the main graph to node on the segment tree I that covers the range at query type 2. And for segment tree II i use in query type 3, i add a directed edge from node which covers the range to vertex v on main graph.
I still not sure about 1 thing. Why we need to build 2 different segment trees for different plan? Because at first, my code only build 1 segment tree that uses for both plans and it produces an incorrect output.
Anyone would help me to understand? Thanks in advance
There should be both a directed edge from a leaf node to its parent and a directed edge from a non-leaf node to its children, or our graph isn't equivalent to the original one. We cannot add them in the same segment tree, so we build two of them and add an directed edge between the corresponding leaf nodes. This is my understanding.
I think these edges are unidirectional, as [l,r]->v == ( [l,(l+r)/2]->v U [1+(l+r)/2,r]->v ) but [l,(l+r)/2]->v != ( [l,r]->v U x ) where x is anything.
If we have [l,r]-w->v and [l,r]-0->[l,(l+r)/2] and [l,r]-0->[1+(l+r)/2,r] then [l,(l+r)/2]-w->v and [1+(l+r)/2,r]-w->v are also true, but we can't add these last two edges in our dijkstra-graph in logn time. We must represent [l,r]-w->v type edges in the second segment tree.
In the second segment tree, the edges will be like these:
[l,r]-w->v
[l,(l+r)/2]-0->[l,r] [1+(l+r)/2,r]-0->[l,r]
We must add seg1[l,l]-0->v and v-0->seg2[l,l] to connect the two segment trees.
Now we have connected both segment trees and all relationships are correctly represented with edges. See that the direction of edges in the segment trees are opposite to each other ( parent to child for query type 2, in first segment tree ) and ( child to parent for query type 3, in second segment tree )
Thanks for your reply. Maybe my expression is not accurate. The directed edge from a non-leaf node to its children is in the first segment tree (for the second type v->[l,r]). The directed edge from a node to its parent is in the second segment tree (for the third type [l,r]->v). These can make sure two real nodes are reachable if and only if there's an edge we get from the input.
Hi
Let me explain it.
[l,r]-w->v represents edge from vertex range [l,r] to vertex v ( 3rd type query ) and has weight w.
If there is a 3rd type query [l,r]-w->v then this implies that
[l,(l+r)/2]-w->v ...(1)
[1+(l+r)/2,r]-w->v ...(2)
But we can't add the edges (1) and (2) in log time, as we have to add edges of their left and right child too recursively. If we don't add edges (1) and (2) ( and their children as well ) then we can't properly represent the relation [l,r]-w->v in our graph when we run dijkstra later. But adding all these child edges takes O(n) per query of type 3.
Surely, the first segment tree will not be able to handle the 2nd and 3rd queries both, as the 2nd query is like v-w->[l,r] which easily represents the relationships of children of [l,r] with v due to the edges [l,r]-0->[left child of [l,r] ] and [l,r]-0->[right child of [l,r] ].
I hope my explanation is clear now.
Ah thanks a lot for your explanation. Now i get the big picture about the idea.
I'm glad you found it helpful :)
can anyone please explain B div2 ?
Can you share your current understanding of the problem, so that we could fill in the gaps? =)
can you explain the second and the third tests
In the second test both groups have a pair of opposite numbers, so these groups cannot be bad.
In the third test case both of the groups can be bad because they don't contain opposite numbers.
I couldn't figure that out why having opposite numbers into a group don't be considered as a bad group?Basically,i want to know where Problem statement said such type of logic? egor.okhterov :)
Here is a part of the problem statement from which that follows: She knows that we are doomed if there's a group such that every member in that group is a traitor.
Let me emphasize the most important part: every member in that group is a traitor.
Now let's look at one group from the second test case:
5 3 -2 1 -1 5As you can see there is a pair of members from universe 1:
"5 3 -2 1 -1 5" — these two guys are from the same universe.
In each universe there are only two people: Rick and Morty. Both Rick and Morty from universe 1 have registered in that group.
We also know from the problem statement that both Rick and Morty cannot be traitors at the same time. Only one of them is a traitor. The other guy is good. That means not all of the guys who registered in that group is a traitor.
Did that help? :)
thank you mrims of persia for beautiful mromlems today
For some strange reason, O(Nlog3N) gives AC with time < 1 sec in problem C div 1. Is this supposed to happen ? Should it pass even in 2 secs ?
Can anyone explain me the complexity of Div2C/Div1A, I did almost the same as explained in the editorial,
My Code
I marked 1st node as Losing for both players then iterated accordingly till there is a change, my complexity is O(n^2*x) where 1<x<n. to my surprise my code passed system test and that too in 300ms.
please someone explain what is wrong with my solution, div2B. http://mirror.codeforces.com/contest/787/submission/25786576
The problem is with the "break" you do when you find a number x and his opposite -x. That's because you haven't already finished reading the input data of that group, so that could make you give a wrong answer later.
thanks
Since the network contains levels(cuts) from S to T with all edges with capacity equal to 1, the total time complexity is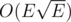
How we get this? The flow network may contain so many edges with infinite capacity.
For Div2A, I still don't quite understand why we only need to check up to 100.
Is it not possible to have something like b +101i = d + 200j?
If the two integers a,b are relatively prime, it's well known that {b,2b,...,(a-1)b} == {1,2,...,a-1} (mod a) We want to find x, y such that ax+by=c, but since there exists 1<=m<=(a-1) such that mb==c (mod a), y=m solves ax+by=c. If a,b are not relatively prime, you can divide each side by gcd(a,b).
In Div.1 E, how to determine which citizens or roads to be chosen after running the flow algorithm(I use dinic)?
Who has understand editorial for 786C — Till I Collapse?
What does "for a fixed l, we define fl(i) to be 1 if l ≤ i and there's no such j that l ≤ j < i and ai = aj otherwise 0. So, if we have a segment tree on every fl, we can use this segment tree to find the first r for an arbitrary k (it's like finding k - th one in this array)." means ?
fl — is array of 0 and 1 ?
"segment tree on every fl" — is segment tree on arrays?
In problem E editorial: what is pr(v, i)? There are inaccurate definition: "For each vertex v in the tree and i (0 ≤ i ≤ lg(n)), we consider a vertex in the tree, this vertex is pr(v, i)."
And when using "parent of vertex v" it meens parent in original tree with chosen beforehand any vertex as root?
My last testcase i.e. number 49 is failing I don't know why...
Can anyone help in debugging
My submission : https://mirror.codeforces.com/contest/786/submission/61284804
Thanks
How to solve C-Till I Collapse with Mo's Algorithm?
I did it by a somewhat similar approach to Mo's Algorithm but not exactly by Mo's Algo.
Heres my strategy:
I couldn't understand your code, can you please explain how you used Mo's algorithm here?
How's the complexity of editorial solution of Div1B $$$ O(nlg^{2}n) $$$ and not $$$ O(nlgn) $$$ as range update in segtree costs only $$$ O(lgn) $$$ ?