In Apr/09/2017, there was a contest in Atcoder.
The contest name is "Square869120Contest #4". Click here
How was it?
Please write and discuss here about impressions and "qustions about solutions".
Thank you for everyone.
It is also advisable to solve those who are not participating or unsolved problems as past problems.
=========================================================================================================
past Square869120Contest
Square869120Contest #4:Click here
Square869120Contest #3:Click here
Square869120Contest #2:Click here
Square869120Contest #1:Click here
Update: If you can, please answer the questionnaire for the improvement to s8pc-5.
About the problem E,I thought a solution during the contest,which the total complexity is O(K*S^3) and passed all of the partial points. Before we choose the stations where the semi-express train stops,find a way to reach every station as fast as possible with greedy. For station i,first,we find the nearest express train station Si and Si+1,second,we reach the station i by the local train from Si or Si+1. Thus,we only need to consider how to arrange semi-express train station between every adjacent Si and Si+1 so that all the stations between Si and Si+1 could be reached by at most X minutes. Since these intervals are independent of each other,we calculate the answer for every intervals such that we can multiply them as the answer. In order to do this,we can define a function Solve(n,l,r) which return the number of different ways that every stations could be reached by at most X minutes while under the limit that if we start from the far left station we shouldn't use more than l minutes and the same as the far right station. First,we enumerate the number of semi-express station that we need to arrange. Second,define f[i][j] as the number of different ways to arrange j semi-express stations in the top i stations satisfies that we could reach them by at most X minutes. When we updating it,just enumerate k that k < i and judge if the stations between k and i could be reached. Notice that the status which could update f[i][j] must be a continuous interval and satisfy the Decision monotony we could use a double ended queue to make it faster Last,by reduce some unnecessary calculation this algorithm can get 630 points. So I wonder that,is the correct algorithm is based on this violent algorithm or change the dp thoughts???
The writer's solution is 2 dimensional dp, dp[i][j] is the number of ways where j = distance between stations, i = (left remaining time) + (right remaining time).
The recurrence relation is:
dp[2i][j] = dp[2i-1][j-1]+dp[2i-1][j-2]+...+dp[2i-1][j-2i]+int(j<=2i+1)
dp[2i+1][j] = dp[2i][j-1]+dp[2i][j-2]+...+dp[2i][j-2i-1]+int(j<=2i+2)
If you use cumulative sum, you can calculate all dp table in O(KS).
Easy implementation. See http://ideone.com/bYCXtT. (The writer of this problem is E869120 but I raised constraints)
Thanks.But can you explain it more detailed?It seems that the code isn't doing what you say...
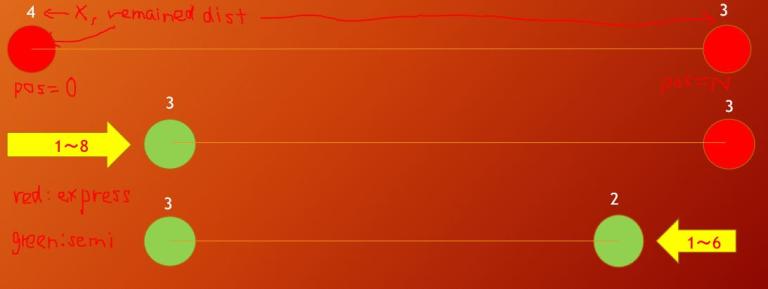
We will define "remain distance", if the shortest path distance from 0 to i is d, the remain distance is X - d (X is the limit of the shortest distance).
You can do leftpush -> rightpush -> leftpush -> rightpush -> leftpush -> ... and amazingly you can enumerate all the ways and there are no collisions of ways.
And, you can return to problem in case of K = 2 (K is the number of , and multiply the results.
In case of K = 2, how can you solve it? This is the clip of my editorial slide (Japanese), and add the little English words. This case is X = 4.
In this case, (left remain dist, right remain dist): (4, 3) -> (3, 3) -> (3, 2), (2, 2) -> (2, 1) -> .
If you want to prune the state and connect left and right semiexpress (or express), you can terminate if d ≤ ld + rd + 1 (let ld = left remain dist, rd = right remain dist, d = number of stations between left and right + 1). That's the meaning of int(j ≤ 2i + 1) and int(j ≤ 2i + 2) (If you don't know the meaning of int(f), f takes true or false and if true return 1 and otherwise return 0).
The meaning of "1-8" and "1-6" is the range of pushing distance, and the number of ways on the picture example is like this (let solve(d, ld, rd) = the number of ways, definition of d, ld, rd said before):
solve(S, 4, 3) = solve(S - 1, 3, 3) + solve(S - 2, 3, 3) + ... + solve(S - 8, 3, 3)
It seems that dp[d][ld][rd] is ok but constructing dp table takes O(SX2), but either ld = rd or ld = rd + 1 are satisfied, so you can do like dp[d][ld + rd], so constructing dp table takes O(SX).
And it seems to process K queries and multiply it, but the answer is already written in the dp table, and the answer is dp[si + 1 - si][2X - 2i - 1] for range between station si and si + 1. (Maybe dp[i][j] definition is little different from before post)
Thanks for your reply.I understand and solve this problem successfully:p
Well, I've been ranting so much these days in CF.. So I thought I should stop ranting, but you've made the place to rant so I'll just write it here.
I started competitive programming in 2014 (10th grade), and this was the first contest which gave "1 2 3 " WA, "1 2 3" WA, and only "1 2 3\n" AC. I remember this was not atcoder's default setting, so I want to hear why you've decided to make it so strict.
Besides, when solving atcoder problems, I remember some contests make solutions without '\n' WA, but some contests don't. What is the exact criteria for these?
Still, kudos for your great efforts. When reading problem FGH, it was clear that you guys were working super hard for them. In 9th grade, I was working hard for escaping Bronze tier in LOL, so you guys are doing very well. Keep up those good things!
I am sorry for that.
First of all, it was bad that "outputting a line break at the end" was not mentioned ... I'm sorry for the inconvenience.
In addition, perhaps in each issue of Atcoder, we are preparing "Output checker", but sorry about the inconvenience caused by "blank / line feed processing" not included in it.
Perhaps the reason is that I have never become "WA because of line breaks / blanks" ... I think it is a matter of experience.
However, since we have learned that the current line feed / blank permission is absent as the "initial value" in Atcoder, we will be careful after s8pc — 5.
Thank you for participating.
Just btw, What is your LOL rank now:P
I stopped playing it immediately after I reached silver. That was feb 2014, so now I don't have any LOL rank
Good job, guys! It was really nice round. You make correct choice, when give many partial points. In such a way, everyone can try to solve as hard version of problem as he want.
I don't understand the solution to the last subtask of problem F. What are the important vertices in the graph?
"Important vertices in the graph" are these:
- Start point of arrow.
- End point of arrow.
- End point of arrow when arrow's direction was changed.
Note: Start point and Goal point is both important too.For example, green cells(vertices) are important.