Given an array of n elements. ‘k’ operations need to be performed on the array.
For each operation start_index, end_index,trim_value is given. One has to trim the value starting from the start_index to end_index inclusive.
If the value at that index is more than or equal to trim value then make it equal to trim_value else leave it as it is. for each A[i] for i between start and end , A[i] = min(A[i],h) .
After performing, ‘k’ such operations find the maximum value of the array.
I have a solution of O(n + k*log(n)). I think it can be optimized to O( n*log(n) ) at least, if not better.
Note: Please try not to use Segment tree or BIT.
Constraints -> n<=10^6 (sure) , A[i] <= 10^6 (Not quite sure of this though)
For Eg. Given array = 7, 2, 8, 5, 1, 6, 4 and k = 3
Following are the k operation (start, end, value) -
1 3 4 => Now the array = 4, 2, 4, 5, 1, 6, 4
3 5 5 => Now the array = 4, 2, 4, 5, 1, 6, 4
4 7 4 => Now the array = 4, 2, 4, 4, 1, 4, 4
So the Maximum value is 4 in the array.
Auto comment: topic has been updated by go_rob (previous revision, new revision, compare).
Auto comment: topic has been updated by go_rob (previous revision, new revision, compare).
I can think of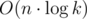
solution using only sets. The constraint on size of each element is not necessary.
You process elements of A one by one, and maintain the operations applied to the current element in a set S. For every element of A, you do the following operations to construct the updated array B, one by one:
B[i] = min(A[i], max(S).first)(if S is empty, just putB[i] = A[i])Now you have the array B that you can use to answer any queries.