Author : zscoder
This is a simple implementation problem. We iterate through all banknotes one by one and check if Oleg can take each of them. If a banknote is at position x, then Oleg can take it if and only if b < x < c. This can be checked in O(1) time. Thus, the total complexity is O(n). Note that the information on the starting position of Oleg is useless here.
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<ll,ll> ii;
typedef vector<ll> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
int a, b, c; cin>>a>>b>>c;
int n; cin>>n;
int ans=0;
for(int i=0;i<n;i++)
{
int x; cin>>x;
if(x>b&&x<c) ans++;
}
cout<<ans<<'\n';
}
Author : zscoder
Let's find the value of xi explicitly. Suppose we make the i-th cut and distance xi from the apex. Then, the ratio of similitude of the isosceles triangle with apex equal to the apex of the carrot and the base equal to the i-th cut and the whole carrot is 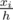 . Since the area of this smaller isosceles triangle is the sum of areas of the first i pieces, which is
. Since the area of this smaller isosceles triangle is the sum of areas of the first i pieces, which is  of the whole carrot. Thus,
of the whole carrot. Thus, 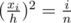 , which is equivalent to
, which is equivalent to 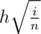 . Thus,
. Thus, 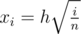 and we can find each xi in O(1) time. The total complexity is O(n).
and we can find each xi in O(1) time. The total complexity is O(n).
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<ll,ll> ii;
typedef vector<ll> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
ll n, h; cin>>n>>h;
for(int i=1;i<=n-1;i++)
{
cout<<fixed<<setprecision(12)<<sqrt(ld(i)/ld(n))*ld(h);
if(i<n-1) cout<<' ';
}
cout<<'\n';
}
Author : zscoder
First, it is clear that Oleg will place 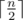 letters and Igor will place
letters and Igor will place 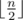 letters. Next, it is clear that Oleg and Igor will both choose their smallest and biggest letters respectively to place in the final string. Thus, we now consider that Oleg places his smallest
letters. Next, it is clear that Oleg and Igor will both choose their smallest and biggest letters respectively to place in the final string. Thus, we now consider that Oleg places his smallest 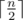 letters and Igor places his largest
letters and Igor places his largest 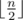 letters.
letters.
Consider the following greedy strategy. When it's Oleg's turn, he will replace the frontmost question mark with his smallest letter. When it's Igor's turn, he will replace the frontmost question mark with his largest letter. At first glance, you might think that this works. However, there's another case that we haven't considered.
Suppose Oleg has the letters {x, y, z} and Igor has the letters {a, b, c}. According to our previous strategy, Oleg will place x as the first letter. However, that's not optimal. He can place his letters at the back and force Igor to place the first letter. The reason is because the largest letter of Igor is not larger than the smallest letter of Oleg. Thus, it is beneficial for Oleg to place his letters at the back and force Igor to place his letters in front.
So, what exactly will the final string look like? We'll look at the moves one by one. If at some point Oleg's smallest letter is still strictly smaller than Igor's largest letter, then both player must put their smallest (largest if it's Igor) letter as the frontmost letter. Why? Suppose not, then on the next turn the other player will occupy that spot with their best (smallest if Oleg, largest if Igor) letter, and the resulting string will be worse for the current player. This proves that greedy is correct in this case.
Now, what if Oleg's smallest letter is not smaller than Igor's largest letter. In this case, both players will want to force the other player to place their own letter at the beginning of the string. It can be proven that in this case, each person will place their current worst (largest if Oleg, smallest if Igor) letter at the back of the string in the optimal strategy. Thus, we can calculate the final string starting from this point and after that reverse this part and combine it with the first part of the string where both players greedily place their best letters in the beginning.
Time Complexity : O(n)
Many people failed on pretest 6 initially because they didn't consider the second case.
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<ll,ll> ii;
typedef vector<ll> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
string ansl;
string ansr;
string s,t;
cin>>s>>t;
sort(s.begin(),s.end());
sort(t.begin(),t.end());
reverse(t.begin(),t.end());
int n = s.length();
deque<char> a,b;
for(int i=0;i<(n+1)/2;i++)
{
a.pb(s[i]);
}
for(int i=0;i<n/2;i++)
{
b.pb(t[i]);
}
bool mode=0;
for(int i=0;i<n;i++)
{
if(i&1)
{
if(!a.empty()&&a[0]>=b[0])
{
mode=1;
}
if(mode)
{
ansr+=b.back();
b.pop_back();
}
else
{
ansl+=b[0];
b.pop_front();
}
}
else //P1's turn
{
if(!b.empty()&&a[0]>=b[0])
{
mode=1;
}
if(mode)
{
ansr+=a.back();
a.pop_back();
}
else
{
ansl+=a[0];
a.pop_front();
}
}
}
reverse(ansr.begin(),ansr.end());
ansl+=ansr;
cout<<ansl<<'\n';
}
Author : AnonymousBunny
Add each vertex to its own adjacency list. Now, we claim that if it is possible to label the cities to satisfy the problem conditions, then it is possible to do so so that for every two cities with the same adjacency list, they're labelled with the same number.
Indeed, if they have the same adjacency list, they must be neighbours. Thus, the difference between their labels is at most 1. Suppose we label the first vertex u with number i and the second vertex v with the number i + 1. Note that since their adjacency lists are equal, a vertex x is a neighbour of u iff it's a neighbour of v. Thus, u and v can't have neighbours with labels i - 1 or i + 2, or else it will contradict the condition. Thus, all neighbours of u and v have labels i or i + 1. Thus, we can safely change the label of the second vertex v to i and the conditions will still hold.
Thus, we can sort the set of adjacency lists of each vertex, and then group the vertices with the same adjacency list together. Suppose there are k such groups. For simplicity, we can create a new graph where each group represent a vertex of the new graph. Connect two groups i and j if and only if there exist some vertex in group i that connects to a vertex in group j. Note that the graph will have at most O(m) edges. Now, if a vertex has degree ≥ 3, we can't assign a number to that vertex properly, as one of its neighbours will not have a label which have a difference ≤ 1 from it. Thus, all vertices in the new graph must have degree ≤ 2. Since it's connected, it must be either a cycle or a path. However, it can be easily seen that there is no labelling if it's a cycle. Thus, it must be a path. Now, we can just assign the labels to the graph from one end of the path to the other end by the numbers 1 to k. Finally, the label of a vertex is simply the label of its group.
This solution can be implemented in 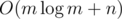 time.
time.
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<int,int> ii;
typedef vector<ll> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
const int N = 300000;
pair<vi,int> adj[N+2];
int ans[N+2];
int lab[N+2];
int lab2[N+2];
set<int> adj2[N+2];
vector<ii> edges;
struct DSU
{
int S;
struct node
{
int p; ll sum;
};
vector<node> dsu;
DSU(int n)
{
S = n;
for(int i = 0; i < n; i++)
{
node tmp;
tmp.p = i; tmp.sum = 0;
dsu.pb(tmp);
}
}
void reset(int n)
{
dsu.clear();
S = n;
for(int i = 0; i < n; i++)
{
node tmp;
tmp.p = i; tmp.sum = 0;
dsu.pb(tmp);
}
}
int rt(int u)
{
if(dsu[u].p == u) return u;
dsu[u].p = rt(dsu[u].p);
return dsu[u].p;
}
void merge(int u, int v)
{
u = rt(u); v = rt(v);
if(u == v) return ;
if(rand()&1) swap(u, v);
dsu[v].p = u;
dsu[u].sum += dsu[v].sum;
}
bool sameset(int u, int v)
{
if(rt(u) == rt(v)) return true;
return false;
}
ll getstat(int u)
{
return dsu[rt(u)].sum;
}
};
deque<int> chain;
void dfs(int u, int p, bool type)
{
if(type) chain.pb(u);
else chain.push_front(u);
int c=0;
for(sit it = adj2[u].begin(); it != adj2[u].end(); it++)
{
int v = (*it);
if(v==p) continue;
if(p!=-1)
{
dfs(v,u,type);
}
else
{
dfs(v,u,c);
c++;
}
}
}
int main()
{
//ios_base::sync_with_stdio(0); cin.tie(0);
int n, m; scanf("%d %d", &n, &m);
for(int i = 0; i < m; i++)
{
int u, v; scanf("%d %d", &u, &v);
u--; v--;
adj[u].fi.pb(v);
adj[v].fi.pb(u);
edges.pb(mp(u,v));
}
for(int i = 0; i < n; i++)
{
adj[i].fi.pb(i);
adj[i].se = i;
sort(adj[i].fi.begin(),adj[i].fi.end());
}
sort(adj,adj+n);
int cnt = 1;
for(int i = 0; i < n; i++)
{
if(i==0)
{
lab[adj[i].se] = cnt;
}
else
{
if(adj[i].fi==adj[i-1].fi)
{
lab[adj[i].se]=cnt;
}
else
{
lab[adj[i].se]=++cnt;
}
}
}
if(cnt==1)
{
printf("YES\n");
for(int i = 0; i < n; i++)
{
printf("%d ",lab[i]);
}
printf("\n");
return 0;
}
DSU dsu(cnt+1);
for(int i = 0; i < m; i++)
{
int u = edges[i].fi; int v = edges[i].se;
if(lab[u]!=lab[v])
{
adj2[lab[u]].insert(lab[v]);
adj2[lab[v]].insert(lab[u]);
dsu.merge(lab[u],lab[v]);
}
}
bool pos = 1;
for(int i = 1; i <= cnt; i++)
{
if(dsu.rt(i)!=dsu.rt(1))
{
pos=0;
break;
}
}
if(!pos)
{
printf("NO\n");
return 0;
}
int d1 = 0;
for(int i = 1; i <= cnt; i++)
{
if(adj2[i].size()>2)
{
printf("NO\n");
return 0;
}
if(adj2[i].size()==1) d1++;
else assert(adj2[i].size()==2);
}
if(d1==2)
{
printf("YES\n");
dfs(1,-1,0);
for(int i = 0; i < chain.size(); i++)
{
lab2[chain[i]] = i+1;
}
for(int i = 0; i < n; i++)
{
printf("%d ",lab2[lab[i]]);
}
printf("\n");
}
else
{
printf("NO\n");
return 0;
}
}
Author : zscoder
First, we solve the problem when no one has any extra turns.
Suppose we're binary searching the answer. Let all the numbers ≥ x be equal to 1 and all the numbers < x be equal to 0. Both players can remove one number from one end of the row. The goal of the first player is to let the remaining number be 1 and the goal of the second player is to leave 0 in the end. If the first player can win, this means that the answer is at least x. Thus, we first try to solve this simpler problem.
We claim that the first player wins if and only if :
n is even and one of the two middle numbers is 1.
n is odd, the middle digit is 1 and at least one of the digits beside the middle digit is 1 (unless n = 1, for which first players wins when the only carrot is labelled 1)
Indeed, once we deduce this, we can easily prove this by induction on n. The proof is just doing casework and considering all possible moves.
Once we have this fact, we realize we don't actually have to binary search the answer. If n is even, the answer is 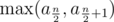 while if n ≥ 3 is odd, the answer is
while if n ≥ 3 is odd, the answer is 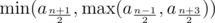 . (If n = 1 then the answer is obviously a1.)
. (If n = 1 then the answer is obviously a1.)
Now, we have to take extra moves into account. Fortunately, it's not very difficult. Having k extra moves just means that Player 1 can choose to start the game in any subsegment of length n - k. Thus, we just have to compute the maximum answer for all subsegments of length n - k for all 0 ≤ k ≤ n - 1. With the formula above, you can find all the answers in O(n) time or even  time if you use sparse table for range maximum query.
time if you use sparse table for range maximum query.
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<ll,ll> ii;
typedef vector<ll> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
int a[300001];
int ans[300001];
int b[300001];
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
int n; cin>>n;
int mx=0;
for(int i=0;i<n;i++)
{
cin>>a[i];
mx=max(mx,a[i]);
}
for(int i=0;i<n-2;i++)
{
b[i]=min(a[i+1],max(a[i],a[i+2]));
}
ans[n-1]=mx;
int odd=n;int even=n;
if(n&1) even=n-1;
else odd=n-1;
mx=0;
for(int i=even;i>=2;i-=2)
{
int l = (i-1)/2; int r=n-i/2;
assert(l<=r);
mx=max(mx,max(a[l],a[r]));
if(i==even)
{
assert(r-l<=2);
if(r-l==2)
{
mx=max(mx,a[l+1]);
}
}
ans[n-i]=mx;
}
mx=0;
for(int i=odd;i>=3;i-=2)
{
int l = i/2-1; int r=n-2-i/2;
assert(l<=r);
if(i==odd) assert(r-l<=1);
mx=max(mx,max(b[l],b[r]));
ans[n-i]=mx;
}
for(int i=0;i<n;i++)
{
cout<<ans[i];
if(i<n-1) cout<<' ';
}
cout<<'\n';
}
Author : hloya_ygrt
We use a segment tree to solve this problem. For each node, it is sufficient to store two arrays : sum[i], denoting the total contribution of the digit i in the current segment (if a digit is in the tens digit then it contributes 10 to the sum and etc...), and also nxt[i], what all the digits i in the current segment are changed to.
Maintaining these arrays is quite straightforward with lazy propogation. When we push an update down a node, we need to update the nxt array of the children. First, we change st[id].nxt[u] to v, where the current update is to change all digits u to v. Then, we change st[id * 2].nxt[i] to st[id].nxt[st[id * 2].nxt[i]], where st[id] is the current node and st[id * 2] is one of the children nodes. (Do the same for the right children). You can see the code if you need more details. Finally, update the sum array of the current segment.
The total complexity of the code is 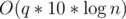 , which is fast enough.
, which is fast enough.
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<ll,ll> ii;
typedef vector<int> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
const int N = 100000;
int a[N+1][10];
struct node
{
int nxt[10];
ll sum[10];
};
node st[N*4+1];
void combine(int id)
{
for(int i = 0; i < 10; i++)
{
st[id].sum[i]=st[id*2].sum[i]+st[id*2+1].sum[i];
}
}
void build(int id, int l, int r)
{
if(r-l<2)
{
for(int i = 0; i < 10; i++) st[id].sum[i]=a[l][i];
for(int i = 0; i < 10; i++)
{
st[id].nxt[i] = i;
}
return ;
}
for(int i = 0; i < 10; i++)
{
st[id].nxt[i] = i;
}
int mid=(l+r)>>1;
build(id*2,l,mid);
build(id*2+1,mid,r);
combine(id);
}
int nxt1[10];
int nxt2[10];
ll sum[10];
void push(int id, int l, int r)
{
memset(sum,0,sizeof(sum));
if(r-l>=2)
{
for(int i = 0; i < 10; i++)
{
nxt1[i] = st[id].nxt[st[id*2].nxt[i]];
nxt2[i] = st[id].nxt[st[id*2+1].nxt[i]];
}
for(int i=0;i<10;i++)
{
st[id*2].nxt[i]=nxt1[i];
st[id*2+1].nxt[i]=nxt2[i];
}
}
for(int i=0;i<10;i++)
{
sum[st[id].nxt[i]]+=st[id].sum[i];
}
for(int i=0;i<10;i++)
{
st[id].sum[i]=sum[i];
st[id].nxt[i]=i;
}
}
void update(int id, int l, int r, int ql, int qr, int u, int v)
{
push(id,l,r);
if(ql>=r||l>=qr) return ;
if(ql<=l&&r<=qr)
{
st[id].nxt[u]=v;
push(id,l,r);
return ;
}
int mid=(l+r)>>1;
update(id*2,l,mid,ql,qr,u,v);
update(id*2+1,mid,r,ql,qr,u,v);
combine(id);
}
ll query(int id, int l, int r, int ql, int qr)
{
push(id,l,r);
if(ql>=r||l>=qr) return 0;
if(ql<=l&&r<=qr)
{
ll sum=0;
for(int i=1;i<10;i++)
{
sum+=ll(i)*st[id].sum[i];
}
return sum;
}
int mid=(l+r)>>1;
return (query(id*2,l,mid,ql,qr)+query(id*2+1,mid,r,ql,qr));
}
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
int n, q; cin>>n>>q;
for(int i = 0; i < n; i++)
{
int x; cin>>x;
int cur=1;
for(int j = 0; j < 9; j++)
{
a[i][x%10] += cur;
x/=10;
cur*=10;
if(x==0) break;
}
}
build(1,0,n);
for(int i = 0; i < q; i++)
{
int type;
cin>>type;
if(type==1)
{
int l,r,u,v;
cin>>l>>r>>u>>v;
l--; r--;
update(1,0,n,l,r+1,u,v);
}
else
{
int l,r; cin>>l>>r;
l--; r--;
ll sum = query(1,0,n,l,r+1);
cout<<sum<<'\n';
}
}
}
Author : zscoder
First, we solve the problem when there're no question marks, i.e. we find a way to calculate the number of good pairs of strings fast for a constant pair of strings A and B.
Call a pair of strings (S, T) where |S| ≤ |T| coprime if S = T or S is a prefix of T, and if T = S + X, then (X, S) is also coprime. (S, T) where |S| > |T| is coprime iff (T, S) is coprime.
If A = B, then all possible strings work. Thus, we assume A ≠ B from now on. We remove the longest common prefix of A and B. Thus, we can assume A[0] ≠ B[0]. Thus, either S is a prefix of T or T is a prefix of S. WLOG, S is a prefix of T. Let T = S + X. Now, A and B consists of only S and X. Using this, we can prove by induction on |S| + |T| that S and T must be coprime.
One important property of coprime strings is that S + T = T + S holds. (again induction works here)
Now, since the strings S and T needs to be coprime, we have S + T = T + S. This allows us to swap any neighbouring Ss and Ts (or 'A's and 'B's) in A and B, as the resulting strings will still be equal. Thus, swapping repeatedly allows us to sort the strings A and B. (the 'A's appear in front and 'B's appear at the back) Let xA, xB, yA, yB denote the number of As and Bs in the first string and second string respectively. If (xA, xB) > (yA, yB), then the answer is 0. We'll handle the case (xA, xB) = (yA, yB) later. Now, assume xA > yA, xB < yB. Thus, we have to solve the equation (xA - yA) copies of S = (yB - xB) copies of T.
Now, let x = xA - yA, y = yB - xB. If x = y, then the solution is S = T. Otherwise, assume x > y. Then, |S| < |T|. So, by comparing, we again have T = S + X, for some nonempty binary string X. Note that S and X must be coprime too, so we can sort the second string as well. We cancel off the Ss on both sides to get (x - y)S = yX. Thus, this means that if (S, T) is a solution for (x, y), then (S, X) is a solution for (x - y, y). Note that repeating this process will eventually lead us to (1, 1). (this process is similar to Euclidean Algorithm)
The answer for (1, 1) is the number of solutions to S = T. Let's denote the solution here as X. Doing some backtracking, we realize that the answer for (x, y) is equal to (X....X (y times), X...X (x times)). Note that we still have the condition |S|, |T| ≤ N, so we can translate this to an appropriate condition on the length of X and the answer is simply the number of binary strings of length not exceeding the maximum possible length of X.
The only case that remains is that (xA, xB) = (yA, yB). In this case, any pair of coprime strings S and T will work. Thus, our task reduces to calculating the number of coprime pair of strings with length not exceeding N.
We claim that the number of coprime pair of strings (S, T) with |S| = p, |T| = q is 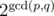 .
.
If p = q the claim is obviously true. Otherwise, we can induct on p + q agin. If q > p, we can write T = S + X and then the number of coprime pairs of (S, T) is equal to the number of coprime pairs of (S, X), which by induction is equal to 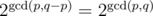 . This proves the claim.
. This proves the claim.
Thus, we just need to compute the sum of 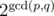 for all 1 ≤ p, q ≤ N.
for all 1 ≤ p, q ≤ N.
Indeed, since N ≤ 3·105, it is enough to count the number of pairs (p, q) with gcd = g for all g.
However, this is quite easy. Let cnt[i] denote the number of pairs (p, q) such that p and q are both divisible by i. Let ans[i] denote the number of pairs (p, q) with gcd = i. Then, 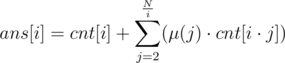 . Thus, this can be computed in
. Thus, this can be computed in  .
.
Now, we need to find out how to calculate the sum of all these values on two strings X and Y with question marks. Handle the case when the two strings become equal separately.
Let's first make a summary of the number of good pairs of strings for constant strings A and B. In fact, note that the formulaes above only depends on (dA, dB), the difference between the number of As in A and B, and the difference between the number of Bs in A and B (note that dA, dB can be negative)
If dA = dB = 0, then the answer is the sum of 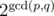 for all 1 ≤ p, q ≤ N, which as we have just saw can be precomputed in time.
for all 1 ≤ p, q ≤ N, which as we have just saw can be precomputed in time.
Otherwise, if dA, dB ≥ 0 or dA, dB ≤ 0, then there are no good pair of strings.
Finally, in other cases, let p = |dA|, q = |dB|. Then, the answer is 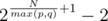 .
.
This also means that we can compute the answer if we know dA and dB very fast. (worst case is  )
)
Now, suppose in the strings X and Y, we have a and b question marks respectively. Additionally, suppose the current difference between the number of As and Bs of these strings is (p, q).
If we choose x and y of the question marks from X and Y to be replaced with As, then the difference between As and Bs in the strings become (p + x - y, q + (a - b) - (x - y)). Let's denote q as q + a - b for simplicity. Thus, the difference is now written as (p + (x - y), q - (x - y)). The values of x and y can be any integer in the range [0, a] and [0, b] respectively. Suppose for all - b ≤ d ≤ a, we know how many ways to assign the question marks have x - y = d. Then, we can iterate through all the ds one by one and compute the answer fast for each d.
Thus, the final hurdle is to calculate the number of ways to obtain x - y = d for all possible d so that 0 ≤ x ≤ a, 0 ≤ y ≤ b. This is just the sum of 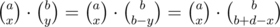 for all 0 ≤ x ≤ a. However, this is equal to
for all 0 ≤ x ≤ a. However, this is equal to 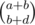 , as the number of ways to choose b + d objects from a + b objects is the same as the sum of the product of the number of ways to choose x objects from the first a objects and the number of ways to choose b + d - x objects from the first b objects for all 0 ≤ a ≤ x. Thus, this value can be computed in O(1) with precomputed factorials and inverse factorials (or you can maintain this value when we iterate through all d).
, as the number of ways to choose b + d objects from a + b objects is the same as the sum of the product of the number of ways to choose x objects from the first a objects and the number of ways to choose b + d - x objects from the first b objects for all 0 ≤ a ≤ x. Thus, this value can be computed in O(1) with precomputed factorials and inverse factorials (or you can maintain this value when we iterate through all d).
Finally, don't forget to take care of the cases where it is possible for both strings to be equal.
The time complexity of the solution is 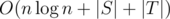 .
.
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<ll,ll> ii;
typedef vector<ll> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
const int MOD = 1e9 + 7;
struct NumberTheory
{
vector<ll> primes;
vector<bool> prime;
vector<ll> totient;
vector<ll> sumdiv;
vector<ll> bigdiv;
void Sieve(ll n)
{
prime.assign(n+1, 1);
prime[1] = false;
for(ll i = 2; i <= n; i++)
{
if(prime[i])
{
primes.pb(i);
for(ll j = i*2; j <= n; j += i)
{
prime[j] = false;
}
}
}
}
ll phi(ll x)
{
map<ll,ll> pf;
ll num = 1; ll num2 = x;
for(ll i = 0; primes[i]*primes[i] <= x; i++)
{
if(x%primes[i]==0)
{
num2/=primes[i];
num*=(primes[i]-1);
}
while(x%primes[i]==0)
{
x/=primes[i];
pf[primes[i]]++;
}
}
if(x>1)
{
pf[x]++; num2/=x; num*=(x-1);
}
x = 1;
num*=num2;
return num;
}
bool isprime(ll x)
{
if(x==1) return false;
for(ll i = 0; primes[i]*primes[i] <= x; i++)
{
if(x%primes[i]==0) return false;
}
return true;
}
void SievePhi(ll n)
{
totient.resize(n+1);
for (int i = 1; i <= n; ++i) totient[i] = i;
for (int i = 2; i <= n; ++i)
{
if (totient[i] == i)
{
for (int j = i; j <= n; j += i)
{
totient[j] -= totient[j] / i;
}
}
}
}
void SieveSumDiv(ll n)
{
sumdiv.resize(n+1);
for(int i = 1; i <= n; ++i)
{
for(int j = i; j <= n; j += i)
{
sumdiv[j] += i;
}
}
}
ll getPhi(ll n)
{
return totient[n];
}
ll getSumDiv(ll n)
{
return sumdiv[n];
}
ll modpow(ll a, ll b, ll mod)
{
ll r = 1;
if(b < 0) b += mod*100000LL;
while(b)
{
if(b&1) r = (r*a)%mod;
a = (a*a)%mod;
b>>=1;
}
return r;
}
ll inv(ll a, ll mod)
{
return modpow(a, mod - 2, mod);
}
ll invgeneral(ll a, ll mod)
{
ll ph = phi(mod);
ph--;
return modpow(a, ph, mod);
}
void getpf(vector<ii>& pf, ll n)
{
for(ll i = 0; primes[i]*primes[i] <= n; i++)
{
int cnt = 0;
while(n%primes[i]==0)
{
n/=primes[i]; cnt++;
}
if(cnt>0) pf.pb(ii(primes[i], cnt));
}
if(n>1)
{
pf.pb(ii(n, 1));
}
}
//ll op;
void getDiv(vector<ll>& div, vector<ii>& pf, ll n, int i)
{
//op++;
ll x, k;
if(i >= pf.size()) return ;
x = n;
for(k = 0; k <= pf[i].se; k++)
{
if(i==int(pf.size())-1) div.pb(x);
getDiv(div, pf, x, i + 1);
x *= pf[i].fi;
}
}
};
NumberTheory nt;
ll modpow(ll a, ll b)
{
ll r = 1;
while(b)
{
if(b&1) r=(r*a)%MOD;
a=(a*a)%MOD;
b>>=1;
}
return r;
}
ll inv(ll a)
{
return modpow(a,MOD-2);
}
ll n;
ll cnt[300001];
ll mob[300001];
ll mobius(ll x)
{
int cc = 0;
for(int i=0;nt.primes[i]*nt.primes[i]<=x;i++)
{
int z=0;
while(x%nt.primes[i]==0)
{
z++;
x/=nt.primes[i];
}
if(z>=2) return 0;
if(z>0) cc++;
}
if(x>1) cc++;
if(cc&1) return -1;
else return 1;
}
ll solve(ll x, ll y)
{
if(x==0&&y==0)
{
for(int i=1;i<=n;i++)
{
cnt[i]=ll(n/i)*ll(n/i);
}
for(int i=1;i<=n;i++)
{
for(int j=2*i;j<=n;j+=i)
{
cnt[i]+=mob[j/i]*cnt[j];
}
}
ll ans = 0;
ll cur = 2;
for(int i=1;i<=n;i++)
{
cnt[i]%=MOD;
if(cnt[i]<0) cnt[i]+=MOD;
//cerr<<i<<' '<<cnt[i]<<'\n';
ans=(ans+(cur*cnt[i])%MOD)%MOD;
if(ans<0) ans+=MOD;
cur=(cur*2)%MOD;
if(cur<0) cur+=MOD;
}
return ans;
}
else if(x>=0&&y>=0)
{
return 0;
}
else if(x<=0&&y<=0)
{
return 0;
}
else
{
x=abs(x); y=abs(y);
ll g = __gcd(x,y);
x/=g; y/=g;
ll k = n/max(x,y);
ll ans = modpow(2,k+1)+MOD-2;
while(ans>=MOD) ans-=MOD;
return ans;
}
}
ll fact[600001];
ll ifact[600001];
ll inverse[600001];
ll choose(ll n, ll r)
{
if(r==0) return 1;
ll ans = fact[n];
ans=(ans*ifact[r])%MOD;
ans=(ans*ifact[n-r])%MOD;
if(ans<0) ans+=MOD;
return ans;
}
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
string s, t;
cin>>s>>t;
cin>>n;
fact[0]=1; ifact[0]=1;
for(int i=1;i<=600000;i++)
{
fact[i]=(fact[i-1]*i)%MOD;
if(fact[i]<0) fact[i]+=MOD;
ifact[i]=inv(fact[i]);
inverse[i]=inv(i);
}
nt.Sieve(300001);
for(int i=2;i<=n;i++)
{
mob[i]=mobius(i);
}
ll sa, sb, sc; //sa = # of As in s, sb = # of Bs in s, sc = # of ?s in s
ll ta, tb, tc;
sa=sb=sc=ta=tb=tc=0;
ll same = 1; //number of ways to fill in ?s such that |S| = |T|
if(s.length()!=t.length()) same=0;
else
{
for(int i=0;i<s.length();i++)
{
if(s[i]=='?'&&t[i]=='?') same=(same*2)%MOD;
else if(s[i]=='?'||t[i]=='?')
{
}
else if(s[i]==t[i])
{
}
else
{
same=0;
}
}
}
for(int i=0;i<s.length();i++)
{
if(s[i]=='A') sa++;
else if(s[i]=='B') sb++;
else sc++;
}
for(int i=0;i<t.length();i++)
{
if(t[i]=='A') ta++;
else if(t[i]=='B') tb++;
else tc++;
}
ll ans = 0;
ll c = 1;
int cntt=0;
for(ll i = sa - ta - tc; i <= sa - ta + sc; i++)
{
if(i==0)
{
ll cc = (c-same)%MOD;
if(cc<0) cc+=MOD;
ans=(ans+(cc*solve(i,sa+sb+sc-ta-tb-tc-i))%MOD)%MOD;
ll tmp = modpow(2,n+1)+MOD-2;
while(tmp>=MOD) tmp-=MOD;
tmp=(tmp*tmp)%MOD;
ans=(ans+(same*tmp)%MOD)%MOD;
}
else
{
ans=(ans+(c*solve(i,sa+sb+sc-ta-tb-tc-i))%MOD)%MOD;
}
if(ans<0) ans+=MOD;
c=(c*inverse[cntt+1])%MOD;
c=(c*(sc+tc-cntt))%MOD;
if(c<0) c+=MOD;
cntt++;
}
cout<<ans<<'\n';
}











What a fast editorial :))) tnx a lot
why problem B。 the input abc aaa
and the output is aab.
why is not aba.
If Oleg didn't put 'b' in last postion in the first turn, then he must put 'b' in a position lower than last position which he doesn't want as he wants to make string lexicographically small. Hence, in the first turn, he will put 'b' in the last position.
Need help for Problem B using Binary Search. I need clear explanation.
Can anybody explain me this line of the editorial of B:
Since the area of this smaller isosceles triangle is the sum of areas of the first i pieces, which is i/n of the whole carrot. Thus, (Xi/h)^2 = i/n
I used the fact that if the ratio of similitude between two similar triangles is r, then the ratio of their areas is r2.
It is said that "It can be proven that in this case, each person will place their current worst (largest if Oleg, smallest if Igor) letter at the back of the string in the optimal strategy." Could someone explain this to me, please?
I also wonder how to prove it,could someone explain??
I've thought a little and changed my mind on this question. I still don't understand why should we occupy the last question mark if it is the least significant position in the sequence. Let p be the number of smallest elements of Oleg's set which are greater than max of Igor set. Why shouldn't we put one of our letters to the position i + p, for instance?(i is the position we are trying our opponent to place letter in)
That's what I thought:
If you have any better letter than your opponent, you should place in the leftmost position. In other case, you should force your opponent to place their letters in the leftmost position, the only way to do that is to place any letter in the last possible position of the string, and the letter chosen is the worst letter, because you want to discard it in the least significant digit — it's nice to notice that you also have the worst letter of the game for you in this case.
Someone please explain me the cutting carrot problem's solution?
You just need to make equations making the area of the first trianlge made by the first cut equal to the overall area over n (and so on).
That is x1*b1/2 = (h*b/2)/n where b1 is the base of the first triangle made by the first cut. b1 is equal to x1 times some constant k. You can determine the exact value of the constant (depending on the relation of b and h) by pitagoras, but this is not necessary. Also notice that this same constant multiples b in the equality h = b*k, therefore you can cross all k's (and all 2's) and get x1*x1 = h*h/n -> x1 = h*sqrt(1/n).
For the second area, between the first and second cut in the trianlgle, you need to make a subtraction of areas of triangles. (x2*b2/2)-(x1*b1/2) = h*b/(2*n) which implies that x2 = h*sqrt(2/n).
By induction you get the editorial's formula xi = h*sqrt(i/n).
can anyone explain how b1 is equal to x1 times some constant k .. Thanks!
In C in 4 test we have: abc && aaa. The answer is aab, but it isn't correct. The answer is aba. First choice of Oleg — put 'a' at the start, sounds good. But Igor will put his 'a' into the end, because he knows, that letters of Igor will be more useful for him in such case. Wtf?
Oleg starts with b to last slot and gets aab which is better for him
Oleg will place b at the end in the beginning, then whatever Igor does Oleg can make aab.
oh, what a misunderstanging, sorry
but in the Naming Company question , is'nt it strictly mentioned that Oleg has to move first.
That's true, but players are free to put their letts in any position that contains a '?'. So Oleg is not necessarily to put his letter in the first or last postion.
problem B
I do not know why i did not use Binary Search.I use a mathematics method.
scanf("%d %lf",&n,&h); double area=h*0.5/n; n--; double s=0.0; int k=0; int m=n; double base=1.0; double tan=1.0/(2*h); while(n--){ double dis=sqrt(base*base-4*tan*area); double x=(base-dis)/(2*tan); a[k++]=h-x-s; s+=x; base=base-2*x*tan; } for(int i=m-1;i>0;--i) printf("%.12f\n",a[i]); printf("%.12f\n",a[0]);
Hi, could someone explain to me what leads to the very first step of the solution of Div 2 D, i.e. "Add each vertex to its own adjacency list"? After reading the tutorial I have no problem to solve it and already got AC, but I was wondering for those who solved it during the contest, does this idea just come out of nowhere or is it a not-well-known trick? During the contest I considered several special cases and tried to categorized vetex by their adjacent neighbors which don't help at all. Are there any similar problems?
A vertex is added to its own adjacency list so that all pairs of vertices which are connected to each other and have the same set of neighbours will have the same adjacency lists.
Lets say a and b are connected by an edge, and they also have the same neighbours c,d,e etc. (excluding themselves). Adj(a) = [b,c,d,e,...] Adj(b) = [a,c,d,e,...]
By adding a vertex to its own adjacency list, in this case, the lists become as follows. Adj'(a) = [a,b,c,d,e,...] Adj'(b) = [a,b,c,d,e,...]
Thansk for your comments, but what confused me here is not "how/why does this solution work", I already understand it and implement it after reading the tutorial. I want to know how those high rating people come to this idea "add a vertex to its adjacent list and group vertex with same adjacent list into one". Because to me it's not obvious or straightforward at all, so I was asking are there any similar problems that use this trick as well.
Can somebody explain to me how the test 5 works on problem C. Like what are the movements of the 2 friends. reddit abcdef answer is dfdeed somebody explain why and how the arrived to this answer, thanks.
Sorted Strings: "ddeirt" , "fedcba"
ansl = "dfd" , ansr = "eed"
d-----
df----
dfd---
dfd--d
dfd-ed
dfdeed
Oh, ok thanks for helping.
Very nice C problem.
Nice !
Wont codeforces take any measures? this guy clearly used two accounts and the rating he won was taken from the other contestants.
UPDATE: Codeforces did take a measure! In his profile there is no sign of participating in this contest (and his rating is the same as before the contest). I wonder if the rating from others changed.
Mind proving that please?
Suppose It is oleg's turn and he knows that the smallest letter he has is bigger or equal to the largest letter Igor has. Thus Oleg would clearly want all of Igor's letters to be ahead of all his letters in the final string. Also, Oleg knows he must place his largest letter somewhere in the resultant string.(Ofcourse when I say largest I only consider ceil(n/2) of his letters). The best place(according to him) for his largest letter,then, is clearly the last available place in the final string. The argument in Igor's case is symmetric.
Why should he begin with placing his worst letter in the end? For example, if he wants Igor's letters to be before his(let Igor has x letters) he should place his best letter to the position i + x as it is much more significant than the last, shouldn't he?
I mean I don't understand why is it better to occupy farthest positions first whether their contribution to lexicographical order isn't that big.
One possible way would be induction and the exchange argument.
Suppose it's Oleg's turn (the argument is the same for Igor's turn)
With our claimed strategy, Oleg will place his largest letter x at the back, forming the string ??????....?x (we ignore all the non-question mark characters in between as they're currently irrelevant)
Suppose Oleg can do better by placing a letter y ≤ x not at the back, so forming the string ???...?y??...?. (If Oleg wants to put a letter at the back, he might as well place his largest one)
By induction hypothesis, we already know what the other question marks should be replaced. We know that the set of letters Igor have after Oleg's current move is still the same, whereas Oleg will not have x in the first case and not have y in the second.
???...?AB....?x
???...?yC....??
Now, you can see that it cannot happen that the second string is less than the first string. It is impossible for any of characters before y to be less than the corresponding letter in the other string by the induction hypothesis (and what Oleg has left is not better than what he would've had if he throw x away). If the character denoted by A is placed by the second player in the optimal strategy, then the first string will be smaller than the second, as all the letters the second player have are smaller. Otherwise, A is placed by the first player and we can see that A is not greater than y or else y would've appeared before A appear and that would mean the matching letter to that y in the second string is larger. However, this implies C is also placed by the first player and B is placed by the second player, and B is not larger than C. If B is equal to C, then we can continue to use the fact that Oleg's letter set after producing the second string is worse than his letter set after producing the first string to see that the second string cannot be strictly smaller than the first.
By induction hypothesis, we already know what the other question marks should be replaced. Could you explain this in detail, please?
Also, due to my poor english or bad mathematics I haven't understood your induction at all, so could you tell where are the basis and inductive steps more explicitly?
What is the inductive hypothesis?
Here you can read about it.
I meant for this particular question..?
For the 5th test case :-
reddit abcdefwhy is the answerdfdeed?In the first turn, oleg could place
dat 1st position, then igor placesfin 2nd position, then oleg placesdat 3rd position, igor placeseat 4th, and in the last step oleg placeseat 6th position, and igor placesdat 5th. Since oleg wants to create a lexicographically smaller string he places his final larger character(than igor) at the last position. Where am i misunderstanding the idea?Igor shouldn't place e at 4th position in the 4th turn, but place d at the last position. Then, no matter what Oleg does, dfdeed is the final string.
Ah, Thank you. i get it now. i misunderstood the editorial.
If I changed my random function "(((ll)rand()<<48)+((ll)rand()<<32)+((ll)rand()<<16)+rand())" to anything else. I would get Accepted on problem D.
rand() in windows is a really excellent function.
random :|
What's wrong with it? On 32-bit systems it returns 15 bits, so you should change 16, 32 and 48 in your function to 15, 30, 45.
The period is short, and vertices get the same hash value. (I think....I haven't tested it in Windows system.
Just use the modern C++11 API (#include <random>), it's much more robust than rand().
It's much more verbose, though. I also prefer to use rand instead of modern random facilities.
Is there any more intuitive approach for the problem D. I find it very difficult to come up with such a solution during the contest. Thanks for your help in advance!
in problem D solution, I cant findout why in the second graph , labels are diffrent ?
if the above statement is not True so why we cant have a vertex with degree>=3 ?
If two vertices have the same labels they must have the same adjacency list (if we include itself in the adjacency list)
Why is this true? I see that vertices with the same adjacency lists have the same label but I can't prove that vertices with the same label must have the same adjacency list.
Let's say there are two vertices u and v that have the same label X but different adjacency lists. It means there is some vertex w that is connected to u/v but not to v/u. Now, w's label must be X - 1, X or X + 1. In any of the three cases, the absolute difference between w's label and the label of the node it is not connected to (u or v) is surely less than or equal to 1, which breaks condition.
Problem setter is just a High school student, even not in university still? WOW, asian people are astonishing at math. They often say that all is just a hard work. But when I work too hard I do not improve better rather get no improvement at all.
Can someone explain why time complexity for C is O(n)? At the beginning of my solution I've sorted both input strings, that's why I think it should be O(nlogn), and I don't see how to do that without sorting... Am I missing something here?
You don't actually need to sort them, given they are english lowercase letters, meaning characters 'a'-'z'. You can store the total count of each character in arrays oleg[26], igor[26] and if any of it is placed to the resulting string, just subtract 1 (and if 0, move the the next/previous non-zero one).
I've got a slightly different solution for C, but it is boring to explain, so here is the code: 27098472 (upd: slightly cleaner version)
Cool but we would request you to explain further
The idea is: if the current player can profit from placing his best letter at the first position (that is, it is strictly better than allowing the other player move there), he must do so. Otherwise, nobody ever has the incentive to move there, hence it will be free until the last move, when the last to move player will place his best letter there. Therefore, we can store who is the first and the last to move, as well as pointers to the best letters of both players, and construct the answer from left to right.
In the code above
t[0]andt[1]are the pointers, andp[0]andp[1]are indices of the first and the last to move players (although in reverse order and negated to make formulas more compact).Well, I didn't know you could call functions which depends on the input outside the main... How does it work? Are all of them called prior to any action of the main function?
Anyone know how to solve F without getting RE on the test case 8? My solution is almost the exact same as the editorial, but I keep getting RE for some strange reason.
My O(NlogN+M) solution for D problem using hashing. http://mirror.codeforces.com/contest/794/submission/27087484
Can you explain your solution?
Let a type of vertex v be the set of vertices that it is connected to, including the vertex v. Each type has its own label.
For example, if we have the edges:
1 2
1 3
The set of vertices of 1 is {1, 2, 3};
For optimal comparing we hash the sets.
From condition |xu-xv| ≤ 1, it's clear that each vertex can only be connected with 3 other types of vertices, one with the same type and label, and two with different types: one with a label+1 and one with a label-1.
When xu-xv = 0, u and v need to be connected to the same set of vertices (be the same type), otherwise the answer is NO.
When |xu-xv| = 1, u and v need to be connected to different sets of vertices (be different types)
For each vertex, we keep two types that it is connected to, D[x] — type of vertex with decreased label and I[x] type with increased one.
Construction and checking:
We start in an arbitrary vertex v, put it a label 5000000 (to have a reserve in decreasing) and check if it isn't connected to more than mentioned 3 types. Put the different types in D[x] and I[x], doesn't matter we way of attributing.
Start a BFS or DFS from v and do the same algorithm.
OK, I got it.
i am not getting how to get to formula in question choosing carrot can someone plzz explain it more
Hi, I'm trying to solve the problem F, using segment tree and simply saving digits in separate arrays, only to got a WA on test 8, tried bunch of debug, do someone give me a hand? 27292086
hi
there is greedy solution with O(n + m) for question D (Labelling Cities).
here is the link
i use hashing, bfs and i do something on neighbours of root.
It seems that there had some mistakes in the data of the problem D.My code didn't make a special judge when the new graph has cycle.For example,if the input data is : 6 6 1 2 2 3 3 4 4 5 5 6 6 1,the output should be a single line containing the string "NO",but my code will got RE of it.However,my code still got AC after submit.Here is the link
Failed to solve F in virtual participation because of the case when x=y. Tricky problem:/
It's a bit late but I've got linear O(N) solution for Labelling Cities (D)
Consider the diameter of the graph. Notice that nodes separate on the diameter can't have a direct edge. So, numbers must run strictly consecutive across the diameter, from one end (smallest) to the other (largest).
If we know one end of the diameter, we can BFS the entire graph starting from it to get the solution (almost)
Normally, finding the diameter of a general graph is O(N^3) with bellman ford. However, notice that all graphs WITH A SOLUTION are special. They must be made up of complete graphs stringed together in a chain, except with perhaps the one edge connecting the two "external" nodes of each component removed.
Therefore it's possible to just BFS from any node to find one end of the diameter, since the entire graph is essentially a chain (all nodes within a connected component have dist 1 to each other anyway)
BFS distance from the one end, to produce colorings. Notice that these colorings are forced once we're outside of the initial fully-connected component.
(* BFS from the other end of the diameter into that initial component to deal with a few edge cases)
(* Also deal with the final edge case where the graph is a [complete graph — single edge])
bcdef
abbbc
what about these two strings ans should be :
step 1: _ _ _ _ d
step 2: c _ _ _ d
step 3: c b _ _ d
step 4: c b b _ d
step 5: c b b c d
but the ans given is: bccdb
can anyone please help me where i am wrong
It should be: step 1: b _ _ _ _ (player 2 may enter c in the first row)
step 2: b _ _ _ b
step 3: b _ _ d b
step 4: b _ c d b
step 5: b c c d b
thanks
Why I am not able to see the editorial? zscoder
can anyone explain me problem B (the carrot one) ?? Thanks!