Tanzir5's blog

How does Dinic's Max Flow compute the blocking flow in O(NM) complexity ?

By Tanzir5, history, 8 years ago, In English

I've been trying to understand Dinic's Max Flow algorithm. I think I've fairly understood how the algorithm works.

In each iteration, you create a level graph using BFS and then find blocking flow in that level graph. You would need O(N) iterations and in each iteration, blocking flow can be found in O(NM) complexity. This is the place where I'm stuck. I've seen some implementations like Stanford Notebook Dinic implementation . But it seems to me that in the worst case you might need O(M^2) complexity to find the blocking flow if you implement the code this way. Can anyone help me to understand why the complexity is O(NM) for finding blocking flow ?

  • Vote: I like it
  • +25
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Hello random people downvoting a valid question. Care to explain ?

→ Reply
»
8 years ago, # |
  Vote: I like it +20 Vote: I do not like it

First you run bfs which is O(M)

Then you run dfs which would run in O(M) but sometimes you return to the origin (when you find path to the end). Suppose between to returns to origin you visited X edges and found path from s to t is Y. It means that you spent X time, and will never run through other X - Y edges (Note that to really skip them there's array of pt in the code)

So, overall time will be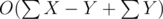 = 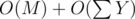But 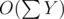is O(NM) because each Y does not exceed N and you do at most O(M) such sub-iterations, because each time you do it, you fill an edge completely.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks a lot. This makes sense.I was actually missing the part of array of pt in the code.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Another thing, I can intuitively understand that in each successive iteration, the length of the shortest path from source to sink would increase. So, since the length can never be more than V, we would need O(V) iterations. Can you please give me some idea about how to prove concretely that the length always increases in each successive iteration?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it +15 Vote: I do not like it

      1) Prove that distance will not decrease for any vertex

      2) Prove what you need

      More elaborate plan in first edit

      → Reply
»
8 years ago, # |
  Vote: I like it +13 Vote: I do not like it

A little bit off topic. I found this code in which it is said that it runs in O(N * M * log(MC)), where MC is maximum edge capacity. Can someone explain why such a complexity?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    This is interesting. I've heard about using dynamic trees to get the above mentioned complexity but this code seems fairly simple. Can you please explain the idea behind it, ADJA ?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      It is standart scaling technique — limiting flow size from up to down. It also can be used in Ford-Fulkerson algorithm.

      → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    I've checked both ADilet JAksybay's implementation and my own O(N^2 * M) implementation for the problem SPOJ FASTFLOW. The runtime of my code is 0.09 seconds whereas the same code with ADilet JAksybay's implementation of Dinic is taking 1.28 seconds. I'm now a bit confused if the complexity stated in the comments of ADilet JAksybay's code is actually correct.

    This is submission with my implementation.

    This is submission with ADilet JAksybay's implementation.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Actually his name is ADilet JAksybay

      → Reply