На этот раз я решил попробовать писать разбор в спойлерах, как уже делал кое-кто из авторов. Буду рад вашим комментариям о том, стало ли лучше.
Задача A. Сдвиги
Темы: динамическое программирование.
Общий комментарий: это первая среди "сложных" задач контеста. В ней можно помочь хорошее знакомство со стандартными задачами на ДП, но довести решение до финального правильного вида все равно непросто.
Решение: пускай мы можем сдвигать не только вправо, но и влево.
Задача B. Число в подарок
Темы: жадность.
Общий комментарий: задача на аккуратность. Требуется учесть много мелких деталей, но в остальном задача вполне решаемая.
Решение: Раз мы максимизируем число, важнее всего понять, насколько большую цифру можно поставить на первое место. Обозначим d первую цифру n.
Задача C. Рекуррентный генератор
Темы: хэширование/строковые алгоритмы.
Общий комментарий: задача несложная, но некоторые решения удачнее других в плане времени работы, памяти и простоты реализации, поэтому продуманный выбор решения мог сэкономить много времени на остальные задачи.
Решение: Для начала поймем, почему последовательность Фибоначчи, определенная в условии, не является 1-рекуррентной.
Задача D. Торговля
Темы: жадность, сортировка, реализация.
Общий комментарий: идея решения сама по себе не является очевидной, но кроме этого требуется большая аккуратность, чтобы избежать проблем с точностью, количеством запросов и всем таким.
Решение:
На этом описание решения по большому счету заканчивается.
Задача E. Прогулка по Манхэттену
Темы: математика, кратчайшие пути в графе.
Общий комментарий: даже если не получается придумать простого математического решения, всегда можно воспользоваться стандартными графовыми алгоритмами. Изи.
Решение:
Задача F. Игра на дереве
Темы: игры, графы, математика.
Общий комментарий: сперва эта задача казалась мне простой, и я ожидал по ней больше правильных решений. Каждая идея по отдельности достаточно несложная, и кода в итоге совсем чуть-чуть. Оказалось, что распутать задачу целиком под силу немногим. Какие у вас впечатления от задачи? =)
Решение:
Буду рад услышать любые ваши мнения в комментариях. Спасибо за участие!



 в том смысле, что никакая буква не встречается в
в том смысле, что никакая буква не встречается в  времени, если отсортировать все участки и делать проверки только для соседних,
времени, если отсортировать все участки и делать проверки только для соседних, времени, если сперва захешировать участки при помощи
времени, если сперва захешировать участки при помощи 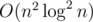 или
или 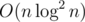 .
.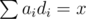 , после чего будем делать небольшие изменения относительно этой конфигурации таким образом, чтобы равновесие зависело от результатов сравнения
, после чего будем делать небольшие изменения относительно этой конфигурации таким образом, чтобы равновесие зависело от результатов сравнения 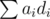 изменится на величину
изменится на величину 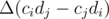 , которая имеет такой же знак, что и разность
, которая имеет такой же знак, что и разность 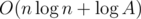 запросов, при данных ограничениях на практике получается около 450.
запросов, при данных ограничениях на практике получается около 450.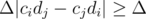 от
от 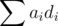 не должно поменяться совсем, а на самом деле из-за погрешностей вещественных чисел оно меняется на очень маленькую величину. В результате, значение может непредсказуемо плясать вокруг
не должно поменяться совсем, а на самом деле из-за погрешностей вещественных чисел оно меняется на очень маленькую величину. В результате, значение может непредсказуемо плясать вокруг 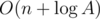 запросов, где
запросов, где 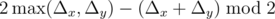 .
.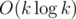 .
.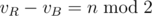 . Это означает, что для оптимальной игры можно с тем же успехом минимизировать
. Это означает, что для оптимальной игры можно с тем же успехом минимизировать 






Random rng = new Random();
Random rng = new Random(228);
Жесть, хорошие тесты, однако!
D and (especially) F are great! Thanks.
По поводу С. Писал на питоне, использовал словарь. Насколько я знаю, они основаны на хеш — таблицах, и по идее итоговая асимптотика должна быть приемлемой, но получил TL. С чем это может быть связано?
UPD Я понял.
Thank you for the great round. I enjoyed to solve A, very interesting problem:D
Let's define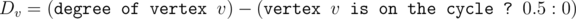 . Then the strategy "choose vertex with the lowest value of Dv among remaining vertices" is optimal. Is this correct?
. Then the strategy "choose vertex with the lowest value of Dv among remaining vertices" is optimal. Is this correct?
And I'll be surprised if the complexity is less than O(POLY·3V) in a general graph.
BTW, I was reminded of Euler Getter from F.
Yeah, looks good to me! I had something complex (and probably wrong), but now I see that this should work. I will probably leave the proof out for now though. =)
I stupidly used map<vector, int> in C and it passed in less than a second))
I also did it, but I don't consider it stupid ;p. However that's why I didn't submit it blindly because I was a little scared about getting TLE.
Why is binary search possible in problem C?
Suppose it is true for a certain length L that all different consecutive L-length tuples have different neighbours to their right(if they exist). I was not able to find any condition mathematically which could show for any length k (k>L), the given sequence is definitely k-recursive.
PS: I tried singe hashing first. It failed. Then I tried hashing with two primes and two big primes. It failed then too. The anti-hash tests were too strong. Can any one tell me which primes did they use for hashing? (in general also).
I think different consecutive L-length tuples arent necessary to have different neighbours to their right. Like a function having different parameter can give out the same value.
It is K-recursive if for every i, j that a[i — k... i — 1] = a[j — k... j — 1], a[i] = a[j].
Now assume It is K-recursive, then it is L-recursive (L >= k). Because first if a[i — k... i — 1] != a[j — k... j — 1], a[i — L... i — 1] != a[j — L... j — 1], so we dont have to consider them. If a[i — k... i — 1] = a[j — k... j — 1], now a[i] must equal a[j], so no matter a[i — L... i — 1] is equal to a[j — L... j — 1] or not, it is still valid.
This editorial is like Christopher Nolan movie. I keep peeling it and new layers keep coming up. At the end I am not sure if I understand the intended story :)
I hope I didn't go too far on the postmodern side in spite of clearness. Would you like something to be explained better?
It's nicely formatted editorial. I had some difficulty following the description for C. I don't understand the transition from Fibonacci series to "if there are two consecutive k-tuples of elements followed by different numbers, then the sequence is not k-recursive". e.g. 1,1,2,3,5,8 seems to match the given condition (1,1 and 2,3 is followed by 5,8) however it is 2-recursive. Source code accompanying the explanation would have been clearer for me.
Take random element, compare it with others and recurse to only one half instead of both (after determining which one). If elements less than this element already contribute at least x than we do not care about order of bigger elements.
Basically it's randomized k-th element algorithm.
Absolutely correct!
In fact it is also possible to adapt standard algorithm searching for median in deterministic way, that works the same way and ensures pessimistic linear complexity, however it would be more complicated to code (but we can make use of nth_element with custom comparator).
Pretty good problems and solutions both. Upvote without any hesitation. Problem A is very instructive to me to think more about LCS. However, I have some confusions about the contest rank. In the rules, it only tells that "Top 512 participants according to the cumulative result of all four elimination stage rounds will receive a contest T-shirt." But, what does the "cumulative results" mean? Does elimination stage show final rank? Sorry for disturbs:(
Yes, the rank is calculated according to the aggregated table at your link.
Here is my derivation for F:
Let's rewrite the score, for kR we can rewrite it as vR — eR; where vR is the number of vertices colored by Red and eR is the number of edges with vertices on both endpoints colored by Red.
Same for kB, we arrive at: (vR — eR) — (vB — eB) which is equal to: (vR — vB) — (eR — eB).
Firstly, observe that the term (vR — vB) is just a constant equal to n mod 2 as both Red and Blue take turns after each other.
Secondly, let's further rewrite the other term, we can observe that edges in the final graph are one of three types:
- eR, eB and eX: edges with different coloring of vertices on their endpoints. We'll rewrite eB as E — eR — eX, where E is the total number of edges. This results in the equation: n %2 — (eR — (E — eR — eX)), which we can simplify as: n %2 + (n -1) — (2*eR + eX).
Finally, we can observe that the last term: (2eR+eX) is exactly equal to the sum of degrees of vertices colored by Red, because, for each vertex colored by Red, all edges connected to it are either of type eR or eX, and edges of type eR are counted twice in the summation of degrees. Remember that the degree of a vertex in an undirected is the number of edges connected to it. So, the goal for Red or Blue becomes to minimize the sum of degrees of vertices colored by them, regardless of previous actions!
Consequently, the optimal choice for Red and Blue will be to color the minimum degree vertex that is uncolored. This results in Red choosing the vertices with the 1st, 3rd, 5th, 7th, 9th, ... (up to nth for odd n or (n-1)th for even n) minimum degree vertices, let's refer to the sum of degrees of these vertices as S.
The final score can be calculated directly as: n%2 + (n-1) — S.
S is calculated after taking the input and sorting vertices based on their degrees, this means complexty is O(n log n).