AtCoder Regular Contest 077 / Beginner Contest 066 Announcement
Two contests AtCoder Regular Contest 077 and AtCoder Beginner Contest 066 will be held at the same time.
You can participate in whichever contest you want. (However, you can't register to both competitions.) The last two tasks in ABC are the same as the first two tasks in ARC.
Time: July 1st (Saturday), 21:00 JST
Duration: 100 minutes
Number of Tasks: 4
writer: nuip
Rating: 0-2799 for ARC, 0-1199 for ABC
The point value are:
ABC: 100 — 200 — 300 — 600
ARC: 300 — 600 — 700 — 1100
We are looking forward to your participation!











Auto comment: topic has been updated by nuip (previous revision, new revision, compare).
Contest will start in 20 minutes.
Why there are no English Editorials for any Beginner Contest?
There is.
I really liked problem D, the relation with Pascal triangle was interesting, but what is the intuition behind this? I found the pattern, but couldn't see how it works.
The equal subsequence can't contain numbers from [p1 + 1, p2 — 1] so you should choose len — 1 numbers from the remaining ones. Btw, there's editorial here(scroll down to english version).
How to solve the last problem?
It seems that I just solved it (5 minutes after the contest because of some stupid bug). I have no idea why it works though...The main observation is that if you had an even string of length 2S with P equal to the maximum length of a prefix strictly smaller than S that is also a suffix, than you go from (S, P) to (2S — P, S — P). This happens by actually getting the half of the given array as Q, and than consequently doing the operation Q += the first S — P elements of Q (here |Q| = S always)And somehow, these numbers seem to be increasing exponentially. To actually get the answer, I did a recursive function that transforms an interval of level L in at most 2 smaller of level L — 1, where level 0 is the given string. However, it failed even on the samples. In order to make it pass, it was enough to keep continuous segments with the same coefficient. You could check my source for better understanding (it has the old, too slow, recursive function too).
How to solve C ?
Notice that for any number a[i], the sequence of positions (position after every operation) is given by the recurrence:
T(n) = T(n-1)+ i*(n%2==0)-(i-1)*(n%2==1)
So, for number a[i], find x = T(n-i+1) and set b[x] = a[i].
What is d in the recurrence ?
Fixed.
Let's think about the small case.
n = 1: a[1]
n = 2: a[2] a[1]
n = 3: a[3] a[1] a[2]
n = 4: a[4] a[2] a[1] a[3]
n = 5: a[5] a[3] a[1] a[2] a[4]
n = 6: a[6] a[4] a[2] a[1] a[3] a[5]
n = 7: a[7] a[5] a[3] a[1] a[2] a[4] a[6]
n = 8: a[8] a[6] a[4] a[2] a[1] a[3] a[5] a[7]
Do you realize it?
Lol, I forgot to handle a[i] > a[i + 1] and a[i] < fav case and it passed more than 10 tests.
Are there any editorial in English?
It is after the Japanese editorial in pdf.
how to solve D ??
The sequence length is n + 1, and each of the integers 1,…,n appears in the sequence. So there is exactly one pair that the number is the same.
First, let's consider about the entire patterns.
The number of patterns that if the contents of two subsequences are the same, they are separately counted, is C(n+1, k).
Second, let's consider about the number of subsequence which is the same.
Consider the pattern of {1, 2a, 3, 4, 2b, 5}. (2a, 2b is both 2.)
- {2a} and {2b} is the same.
- {1, 2a} and {1, 2b} is the same.
- {2a, 5} and {2b, 5} is the same.
- {1, 2a, 5} and {1, 2b, 5} is the same.
So, 3, 4 (=between 2a, 2b) isn't choosed in these subsequence.In summary, the answer is C(n+1, k) — C((l-1)+(n+1-r),k-1) for each k. C(n, r) means nCr.
(l is the smaller index which is the same, and r is the larger index which is the same, in 1-indexed. In example of {1, 2, 3, 4, 2, 5}, l=2 and r=5.)
thanks a lot for your easy explanation :D & another request how to solve E ??
In problem E:
Let p[i] be the benefit of favorite brightness is i.
p[i] can calculate for following method:
So, you should imprementate following query:
This can be imprementate in following method:
This is example of query (3, 6):
Let r be the cost if there were no favorite number.
The answer is r — max(p[1] + p[m+1], p[2] + p[m+2], p[3] + p[m+3], p[4] + p[m+4], ..., p[m] + p[m+m]).
Thank you for reading. Sorry for poor English.
sorry for late reply ... i don't understand why p[3] += 1, p[5] += 3. 1 -> 3 -> 4 -> 5 so p[3] += 3 and 1 -> 5 so p[5] += 1, is n't it?
The reason is:
Sorry for inconvenience, and my poor English.
thanks a lot .. now i get it :) and finally AC :)
Can somebody provide me a working code of searching big binomial coefficients. I was googling for it during half of the contest, and found invalid code
http://e-maxx-eng.appspot.com/combinatorics/binomial-coefficients.html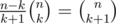
you can use some formulas
for problem D,
http://e-maxx-eng.appspot.com/algebra/module-inverse.html
or precalculate all k!(mod M) and k! - 1(mod M) for k ≤ N in O(N)
You C++ code, you can check this and this.
For Python code, you can check this
Thanks!
Can someone elaborate on how to solve E with two prefix sums