Долго думал над этими задачами,в итоге так и не решил их. Хотелось бы узнать возможные идеи решений.
1) http://acm.timus.ru/problem.aspx?space=1&num=1872 Решаю так. Во-первых, жадно ищу решение: сортирую s[]-размер офисов, на каждом шаге делаю срезки отрезков [ai,bi] по s[i] и среди полученных отрезков выбираю для s[i] отрезок с наименьшей длиной. Этому отрезку k ставлю в соответствие s[i]: inv[k]=i. Во-вторых, если решение есть, проверяю единственность: строю орграф g[][]. Для каждого s[i] ищу те отрезки j, где aj<=s[i]<=bj и inv[j]!=i (каждому отрезку соответствует офис inv[j]). Если условия выполнены=> g[i][inv[j]]=true. В-третьих, поверяю наличие цикла в g[][]: он существует <=> решение не единственно.
Код с WA29:
const int nmax = 1005;
int a[nmax], b[nmax], s[nmax], inv[nmax];
int aa[nmax], bb[nmax], cl[nmax];
bool used[nmax];
bool g[nmax][nmax];
int n, cycle_st;
void QSort(int L, int R);
bool Exist();
bool dfs (int v);
int main()
{ cin>>n; for(int i=1;i<=n;i++) cin>>s[i]; QSort(1, n); for(int i=1;i<=n;i++) cin>>a[i]>>b[i];
if(Exist())
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
g[i][j]=false;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(inv[j]==i) continue;
g[i][inv[j]]=(a[j]<=s[i] && s[i]<=b[j]);
}
}
for(int i=1;i<=n;i++) cl[i]=0;
cycle_st = -1;
for (int i=1; i<=n; i++)
if (dfs(i)) break;
if (cycle_st!=-1) cout<<"Ask Shiftman for help.";
else
{
cout<<"Perfect!"<<endl;
for(int i=1;i<=n;i++) cout<<inv[i]<<" ";
}
}
else cout<<"Let's search for another office.";
return 0;
}
bool Exist()
{
for(int i=1;i<=n;i++) used[i]=false;
for(int i=1;i<=n;i++) aa[i]=a[i], bb[i]=b[i];
for(int i=1;i<=n;i++)
{
int k=-1;
for(int j=1;j<=n;j++)
{
if(used[j]) continue;
if(bb[j]<s[i]) return false;
if(aa[j]<s[i]) aa[j]=s[i];
if(aa[j]==s[i] && (k==-1 || bb[k]>bb[j])) k=j;
}
if(k==-1) return false;
used[k]=true;
inv[k]=i; //k->s[i]
}
return true;
}
bool dfs (int v)
{
cl[v] = 1;
for (int j=1; j<=n; j++)
{
int to = j;
if(!g[v][j]) continue;
if (cl[to] == 0)
{
if (dfs (to)) return true;
}
else if (cl[to] == 1)
{
cycle_st = to;
return true;
}
}
cl[v] = 2;
return false;
}
void QSort(int L, int R)
{
int X=s[(L+R)/2];
int i=L, j=R;
while(i<=j)
{
while(s[i]<X) i++;
while(s[j]>X) j--;
if(i<=j)
{
int Y=s[i]; s[i]=s[j]; s[j]=Y;
i++, j--;
}
}
if(L<j) QSort(L,j);
if(i<R) QSort(i,R);
}
2)http://acm.timus.ru/problem.aspx?space=1&num=2055 Решать не решился, поскольку нет ясных мыслей. Насколько понимаю, для начало нужно отсортировать рёбра, затем найти минимальное остовное дерево. Затем на каждом шаге выбрасывать ребро наименьшего веса и вновь искать минимальное остовное дерево(с рёбрами, у которых вес >= веса выброшенного ребра). Непонятно, можно ли быстро искать новое остовное дерево, если уже большая часть была построена.










Первая задача:
Чтобы найти решение, если оно есть, достаточно первой комнате сопоставить проект с наименьшим концом (и так далее). Чтобы проверить единственность, достаточно попробовать поменять местами O(N) пар проектов, которые были кандидатами с двумя наименьшими концами (для каждой комнаты).
Доказательство: рассмотрим первую комнату в найденном ранее решении, после которой остальной ответ находится однозначно. Чтобы получить неоднозначность, достаточно текущий проект попробовать поменять со следующим наименьшим по длине конца (среди еще не использованных и покрывающих текущую комнату). Поскольку остальной ответ найден однозначно, то при уменьшении конца следующего проекта новых расстановок появиться не может (иначе они бы подходили и для старой конфигурации с более длинным концом подмененного проекта).
Это можно реализовать за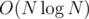 .
.
Вторая задача:
http://mirror.codeforces.com/blog/entry/18944
Насколько понимаю комнаты сортируются по неубыванию(это обозначает, что комната "первая"?). "Наименьший конец" видимо правый? Я также где-то год назад строил решение(да и сейчас срезка делает то же самое) и проверял неоднозначность между проектами, выбранными для офиса i и i+1(эти пары имелись ввиду?). В итоге дальше 6 теста не ушёл.
При рассмотрении i-ой комнаты для нее могут быть несколько проектов-кандидатов, из которых выбирается проект с наименьшим правым концом. Чтобы проверить на неоднозначность, нужно запомнить, какой проект был при этом вторым кандидатом (со вторым наименьшим правым концом) и попробовать в конечном решении их поменять местами.