Problem
Given (x+a1) * (x+a2) * (x+a3) * ... * (x+an), find the coefficient of the term x^k.
In the case of n, k <= 10^5, one way to approach the problem is to use FFT to convolute the terms layer by layer, by eventually raising the maximum power of the terms. (i.e. evaluate the terms grouped in two, four, eight etc. terms) The time complexity of this approach is around O(N*log^2(N)).
In another case where k << n, where k is way smaller than n, or in this case of: (a1*x^k + a2* x^(k-1) + .... + ak) * (b1*x^k + .... + bk) * (c1*x^k + ... + ck) * ..... (n polymials of x^k)
Where O((n*k)log^2(n*k)) is on the verge of risking TLE
I wonder if it is possible to trim the terms so that we don't have to evaluate beyond k <= 2^i terms as if we are convoluting the polynomials with brute force.
As all the original terms have effect on all values after FFT, I assume that one could not naively extract the least significant 2^i terms from the FFT array, so inverse FFT should be applied before trimming (And O(nlogn) isn't too expensive anyways). Yet, I would like to know if there exist an approach which works around this step.
Inspired by: https://www.hackerrank.com/challenges/permutation-equations
There exists a solution which involves finding the coefficient of (x+n-2) * (x+n-1) * ... (x+2) where k <= 60.











I don't understand what do you want to do :(
In short, my aim is to find the x^k term of
(x+a) * (x+b) * (x+c) * ... (x+z)
In trivial case this can be done by just merging the elements with FFT, as if the elements are leafs of a segment tree:
(Picture made by Al.Cash)
So at each layer the power of the polymial will grow by a factor of 2. Yet, we know that terms larger than x^k is no influence on the final answer, and if k is given to be a rather small number, it may be a wise idea to just trim the polymial, and don't care about stuff beyond x^k.
This brings me thinking if there's a convenient way of deleting elements larger than x^k for terms that have gone through FFT, as I reckon that the terms are inter-related.
So why don't you use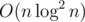 solution using this tree?
solution using this tree?
I am just curious if there exists a way to take advantage of the small k in case if I am facing some other weird situations. (Though I understand O(nlog^2n) is decent enough in most situations)