| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 165 |
| 2 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 4 | adamant | 160 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
Given a sequence of n integers, you have to find out the non-decreasing subsequence of length k with minimum sum. If no sequence exists output -1.
Examples:
Input : [58 12 11 12 82 30 20 77 16 86], k = 3 Output : 39 {11 + 12 + 16}
Input : [58 12 11 12 82 30 20 77 16 86], k = 4 Output : 120 {11 + 12 + 20 + 77}
Input : [58 12 11 12 82 30 20 77 16 86], k = 5 Output : 206
If you are looking for a solution than here
what's your expected time complexity?
In my article which I wrote, the time complexity is O(n^2*k).
Looks like O(N^2*K) to me.
let dp[i][j] represents that we pick i-th number, we get a non-decreasing subsequence which has a size of j, the minimum sum of it.
so naively u can solve it in O(n2 × k)
with bit/range tree you can optimize to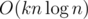
i think?
I know, I was talking about the code from the blog this guy linked. Still, your comment may be helpful for the one asking the question.
gg i just realized that i replied to the wrong person..sry
Can you explain first method please?
Can you explain please?
I am expecting knlogn? Is it possible?
Let's go with i through our array and store k Fenwick trees to find minimum of prefix. Get(bit[j], x) returns minimum sum of non-decreasing subsequence of length j which last element is not greater than x.
Now we want to continue some sequences with our a[i]. For a certain sequence length j we can make sequence of length (j + 1) with minimum sum S = Get(bit[j], a[i]) + a[i], then minimise(bit[j + 1], a[i], S). Correct me if i'm wrong.