This article will be presenting a rather classical problem that can be solved using deques, along with an extension that allows you to solve the problem in its more general multi-dimensional case. I have decided to write this article after this discussion on 2D range-minimum query.
The article will be mainly based on this following problem:
You are given an array of numbers A[] of size n and a number k ≤ n. Find the minimum value for each continuous subarray of size k.
We will be now focusing on the linear-time solution to this problem.
Solution:
Consider sweeping from left to right through the array. At every moment we keep a list of "candidates" for minimum values throughout the process. That means that at each moment, you have to add one element to the list and (potentially) remove one element from the list.
The key observation is that, during the sweep line process, we find two values A[i] and A[j] which have i < j and A[i] ≥ A[j], then we can safely discard A[i]. That is because, intuitively, A[j] will continue to "live" in our sweep line more than A[i], and we will never prefer A[i] instead of A[j].
We should now consider pruning all the "useless" values ("useless" as in the statement above). It is easy to see now that doing this will lead to a strictly increasing list of candidates (why?). In this case, the minimum will always be the first element (O(1) query).
In order to insert an element to the back of the pruned candidate list, we will do a stack-like approach of removing all elements that are greater than it, and to erase on element, we just pop the front of the list (if it is not already removed).
This is a well-known approach for finding minima over fixed-size continuous subarrays. I will now present an extensions that allows you to do the same trick in matrices and even multi-dimensional arrays.
The multi-dimensional extension
Problem (2D):
You are given an matrix of numbers A[][] of size n × m and two numbers k ≤ n, l ≤ m. Find the minimum value for each continuous submatrix of size k × l.
Solution:
Consider the matrix as a list of rows. For each row vector of A, use the 1D algorithm to compute the minimum value over all l-length subarrays, and store them in ColMin[][] (obviously, ColMin[][] is now a n × (m - l + 1)-sized matrix).
Now, consider the new matrix as a list of columns. For each column vector of ColMin, use the algorithm to compute the minimum value over all k-length subarrays, and store them in Ans[][] (of size (n - k + 1) × (m - l + 1)).
The Ans[][] is the solution to our problem.
The following picture shows the intutition behind how it works for computing Ans[1][1] for n = 5, m = 7, k = 3, l = 4 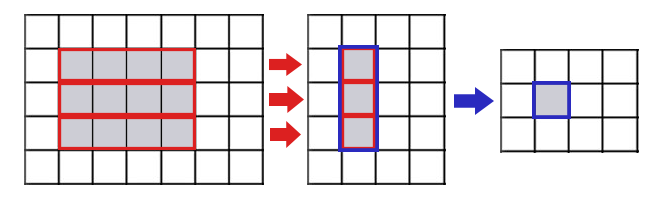
The pseudocode is as follows:
def solve_2d(M, k, l):
column_minima = {} # empty list
for each row in M.rows:
# We suppose we have the algorithm that solves
# the 1D problem
min_row = solve_1d(row, l)
column_minima.append_row(min_row)
ans = {}
for each col in column_minima.cols:
min_col = solve_1d(col, k)
ans.append_col(min_col)
return ans
Note that the pseudocode is (deliberately) hiding some extra complexity of extracting rows / columns and adapting the 1D algorithm to the 2D problem, in order to make the understanding of the solution clearer.
The total complexity of the algorithm can be easily deduced to be O(n * m)
Multi-dimensional case analysis
The solution can be extended to an arbitrary order of dimensions. For a d-dimensional matrix of size s1, s2, ..., sd, the time-complexity of the problem is O(d * s1 * ... * sd), and the memory complexity is O(s1 * ... * sd). This is much better than other algorithms that do the same thing on non-fixed size submatrices (e.g. multi-dimensional RMQ has O(s1 * ... * sd * log(s1) * ... * log(sd)) time and memory complexity).
Finding the best k minima
The deque approach itself is limited in the sense that it allows you to find only the minimum value over the ranges. But what happens if you want to calculate more that one minimum? We will discuss an approach that I used during a national ACM-style contest where we were able to calculate the best 2 minima, and then argue that you can extend to an arbitrary number of minimum values.
In order to store the lowest 2 values, we will do the following:
Keep 2 deques, namely D1 and D2. Do a similar algorithm of "stack-like popping" on D1 when you add a new element, but instead of discarding elements from D1 when popping, transfer them down to D2 and "stack-like pop" it.
It is easy to see why the lowest 2 elements will always be in one of the two deques. Moreover, there are only 2 cases for the lowest two elements: they are either the first two elements of D1, or the first elements of D1 and D2 subsequently. Checking the case should be an easy thing to do.
The extension to an arbitrary number of minima is, however, not so great, in the sense that the complexity of this approach becomes O(n * k2) for a n-sized array, currently bottlenecked by the number of elements you have to consider in order to find the first k minima. [Maybe you can come up with a cleverer way of doing that?]
Useful links
This is the problem I referred to above: http://www.infoarena.ro/problema/smax. I recommend trying to think it through and implementing it, and translating the statement via Google Translate or equivalent.











Auto comment: topic has been updated by bicsi (previous revision, new revision, compare).
Another (quite standard) way to solve the original problem:
We need a queue with "get a minimum" operation. We can simulate a queue with two stacks. Stack with minima is easy: we just need to store pairs (value, minimum of values below this).
Finding best k minima can be solved in the same way. Stack with k minima is not harder: just store k minima of values below this. It obviously work in O(nk).
That is true, however I have compared some time ago this approach with the deque one, and it seemed that the queue was not only more memory-intensive but also noticeably slower. However, the fact about the complexity is true.
At the same time, I realized that the complexity I mentioned was overshot, as you can find out the first k elements of k sorted arrays in O(k * log(k)) (using a priority queue)
Could you explain in more detail how to solve the original problem please? I don't understand what "minimum of values below" means.
Queue modification — using two stacks ( method 3 )
https://cp-algorithms.com/data_structures/stack_queue_modification.html
: just store k minima of values below this. It works in $$$O(nk)$$$.
Can anyone explain how to find $$$k$$$ minima using this approach?
UPD: Is it like storing tuples (value, 1st min, 2nd min, ..., kth min) which leads to amortized $$$O(k)$$$ for push and pop operations?
Good problem for practice: IOI 2006 B. Pyramid.
Where can I submit this problem ? Thanks in advance :)
http://wcipeg.com/problem/ioi0612
Yet another good problem where you can practice is 15D - Map, but be careful if you use Java, because even if you'll try to resubmit accepted solutions, you (in most cases) will have TLE 11.
The following is an O( n ) algorithm for solving the 1-dimensional min/max problem without using a deque.
pair< long long, long long > min_subarray_sum( const int A[], const size_t n, const size_t k ) {
long long initial = A[ 0 ]; for( size_t i = 1; i < k; i++ ) initial += A[ i ]; if ( k < n ) { long long delta = A[ k ] - A[ 0 ]; pair< long long, long long > optimal_delta; for( size_t i = k + 1, j = 1; i < n; i++, j++ ) { delta += A[ i ] - A[ j ]; if ( delta < optimal_delta.first ) optimal_delta.first = delta; if ( delta > optimal_delta.second ) optimal_delta.second = delta; } pair< long long, long long > answer; answer.first = answer.second = initial; if ( optimal_delta.first < 0 ) answer.first += optimal_delta.first; if ( optimal_delta.second > 0 ) answer.second += optimal_delta.second; } return answer;}
The 2-dimensional problem can be solved in O( m n ) using Summed-area Tables introduced by Crow in 1984 [1].
Reference
[1] Crow, F.C., 1984. Summed-area Tables for Texture Mapping, in: Proceedings of the ACM 11th Annual Conference on Computer Graphics and Interactive Techniques, pp. 207–212. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.124.1904&rep=rep1&type=pdf
It may be helpful and useful that codeforces develops it like/dislike voting if possible to enable a voter to include an optional note explaining the reasons for liking/disliking a comment.
I used a similar idea to solve Pyramid from IOI2006
I solved the same question in JUNE CHALLENGE 2016 on Codechef.
Problem
Here is my AC submission using the same idea:
Code
tweety You explained this to me just before the blog was released !!! Wizard
bicsi is working for the NSA confirmed
Yet another method for solving the original problem:
Let's call every element which has an index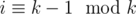 special. For every special element Ai we memorise the minimum for subarrays with indices [j, i], where i - k < j ≤ i and (i, j], where i < j < i + k. Since every query has exactly one special element inside its boundaries, we can easily answer the query as query(l, r) = min (query(l, i), query(i + 1, r)), where i is the special element inside the query. This gives linear space and time complexity.
special. For every special element Ai we memorise the minimum for subarrays with indices [j, i], where i - k < j ≤ i and (i, j], where i < j < i + k. Since every query has exactly one special element inside its boundaries, we can easily answer the query as query(l, r) = min (query(l, i), query(i + 1, r)), where i is the special element inside the query. This gives linear space and time complexity.
This can be extended to any number of dimension d with a complexity of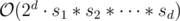 . With k minimums the complexity should be
. With k minimums the complexity should be 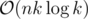 if we use priority queues.
if we use priority queues.
As a bonus the same algorithm can also be extended to give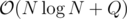 complexity for the standard minimum query problem with no constraints for l and r by having special elements with steps 1, 2, 4, 8... (every query can be answered in constant time since there is at least one step where there are between 1 and 2 special nodes inside the boundaries).
complexity for the standard minimum query problem with no constraints for l and r by having special elements with steps 1, 2, 4, 8... (every query can be answered in constant time since there is at least one step where there are between 1 and 2 special nodes inside the boundaries).
Decompose the matrix into blocks of k × l, and get the prefix sums respecting the upperleft, upperright, lowerleft and lowerright corners. All queries can be calculated using 4 such sums.
Of course, one-dimensional version can be solved this way as well.
The downside is that for k-dimensional version a constant factor of 2k is required.
For "best k minima", you can store the k smallest elements in each prefix sum. You can do the addition and subtraction for on a data structure storing "k smallest elements".
With an appropriate data structure, I think a complexity of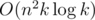 can be reached.
can be reached.
I don't get how you can find the minima/maxima using prefix sums. Can you explain it a bit?
For the "k-minima" case, it may just be better to just use a persistent set data structure (e.g. treap). This lets you find the k-minima for all fixed-size arrays of an n-sized array in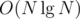 time, irrespective of the value of k (though actually getting the minima explicitly takes O(NK) time).
time, irrespective of the value of k (though actually getting the minima explicitly takes O(NK) time).
Here is a problem to find Minima and Maxima of each sub array of size k in a 1D array of size n: Sliding Window
Thank you so much, I learnt how to apply the 1D sliding window minimum algorithm and transform it into the 2D sliding window algorithm from this blog! This is the problem that I practiced on. I know that since the problem only deals with 2x2 squares, we can do simple brute force, but I was imagining if it was 100x100 squares then we definitely need something like this to speed it up.
Related Problem : https://mirror.codeforces.com/contest/1195/problem/E
Link to my code : https://mirror.codeforces.com/contest/1195/submission/57249978
They’re as related as a Habsburg couple lol
https://atcoder.jp/contests/abc228/tasks/abc228_f is a good practice problem for this technique.
It was a good problem, thank you very much! ^_^
I also noticed that this blog had no C++ code, so here goes my inefficient implementation: