Do you really hate tree rotations? This blog post is for you!

Recently, I've been solving 768G - The Winds of Winter and I came up with a solution which is so ridiculously overengineered that I think it deserves its own blog post!

I don't want to go over all the details of the solution. Instead, I want to demonstrate a nice way to implement and apply Persistent Set and Persistent Array data structures and share a few ideas some may find interesting.

Basically, what I wanted to do is compute for each node x of the rooted tree a set, which would contain the sizes of all subtrees of x. In other words, if we denote sz(y) — the size of the subtree rooted at y, I want to compute the set 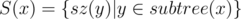for all x. We also want this set to have some lower_bound and upper_bound functionality.

Obviously, just storing these sets in a normal way would require O(n²) memory, so we need another approach. Let's use the same idea that we use when building persistent arrays. A persistent array of size 2^k, k > 0 will just have two pointers to persistent arrays of size 2^k - 1. A persistent array of size 1 will only store data. Our persistent set will be implemented as a persistent array of size at least N whose only elements are 0, 1. Positions at which there is an element shall have value 1, others shall have 0. In addition to the two pointers, each array node will also store the sum of all values. Basically our structure looks a lot like a persistent segment tree. This will allow us to implement lower_bound and upper_bound in . I used class templates to save some memory — this is another interesting idea and a topic on its own.

When you want to insert a number into the set, you don't actually insert it into the set, instead, you create a copy of the set and insert it there. The copying will create additional nodes and will take time. Here's the code:

this_t* insert(int x) {
  this_t* tmp = new this_t(*this);

  if (x < H)
    tmp->left = tmp->left->insert(x);
  else
    tmp->right = tmp->right->insert(x - H);

  tmp->total = tmp->left->total + tmp->right->total;
  return tmp;
}

this_t is the alias for pa<T, order>, the data type of the class for persistent sets. This is basically a persistent array of length 2^order. The first line just creates a shallow copy of the set the we are in. H is equal to half of the size of the current set. If x is less than this number, it means that this new value should be inserted into the left half. Otherwise, insert it into the right half. Again, insertion does not change the original but returns a copy, so we store that copy into tmp->left or tmp->right. We then recompute the total and return the temporary variable. Simple as that! The stopping condition is implemented in the class pa<T, 0>, see my submission 29446581 for more details.

But this is not all! We also need to be able to quickly merge two sets in our original problem! This appears impossible to do efficiently at first, but is actually quite simple and works very fast under some circumstances.

Let's see how we can merge (find the union of) two sets A and B. If one of the sets is empty, we return the other one. Otherwise, just merge the left half of B with the left half of A and the right half of B with the right half of A. Now you're probably asking yourself, how does this even make sense? This is obviously O(n) — and you're right, but, in the original problem, you will be merging small sets most of the time, and when one of the sets you merge is small (let's say it has g elements), this operation will create at most 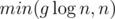new nodes and take 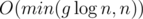time. To understand this, think of what happens when one of the sets has 1, 2, or 3 elements.

Here's the code:

this_t* merge(this_t* arr) {
  if (arr->total == 0)
    return this;

  if (this->total == 0)
    return arr;

  this_t* tmp = new this_t(*this);
  tmp->left = tmp->left->merge(arr->left);
  tmp->right = tmp->right->merge(arr->right);

  return tmp;
}

When we calculate the sets on a tree, each set element will be merged into another set at most times so the complexity (both time and memory) is . You now have access to all the sets, for each node.

Last, but not least, let's see how lower_bound is computed. This, of course, does not create new nodes and should take time. We define lower_bound(x) as the smallest element y in the set such that y ≥ x. If such an element does not exist, we return the capacity of the set. Here's one possible implementation:

int lower_bound(int x) {
  if (total == 0)
    return 2*H;

  if (x < H) {
    int p = left->lower_bound(x);
    if (p == H) {
      return H + right->lower_bound(0);
    else
      return p;
  } else
    return H + right->lower_bound(x - H);
}

The problem here is that we sometimes call lower_bound in both directions. Fortunately, it is not so tragic, the actual complexity here really is . Why is that so? If the lower bound y for x does not exist, let's take y = N - 1 where N is the capacity of the set. We'll only visit array vertices which correspond to array segments which contain x or y and there's at most 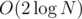of them. We may also visit some others but we will exit immediately as their total is 0.

This concludes the tutorial for this implementation of persistent sets.

But why didn't you just use a segment tree for the problem? After all, you are given a rooted tree, you can flatten it by assigning DFS numbers...

As it turns out, the sets of sizes of subtrees of nodes are not the only thing I needed to compute. I also needed to compute 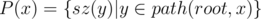, and also 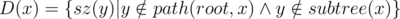. Also, I wanted to try a new approach and see if it's efficient enough. And as it turns out, it is! :)

Here's the code: 29446581. Unfortunately, many comments are in Serbian and some names are meaningless.

Remark 1. It's also relatively easy to implement the order statistic query (find the kth largest element in the set).

Remark 2. You can also extend this to a multiset or a map<int, ?>.

Remark 3. You can save even more memory by delaying the creation of a subarray until it is needed, similar to the implicit segment tree. This allows us to create sets which can contain the full range of integers or even long longs, not just ones in a relatively small range, like 10⁵.

Remark 4. You can accelerate finding the union or intersection of sets if you also store a hash value of each subarray. Then, only merge two sets if their hashes differ. This works particularly well if you often need to merge similar sets (those which differ in only a few elements). In the original problem this was not needed but it's a nice idea nonetheless.