Блог пользователя totsamyzed

Codeforces Round #429 [Editorial]
Автор totsamyzed, 7 лет назад, По-русски

Щедрый Кефа — Adiv2
(Авторы: Mediocrity, totsamyzed)

Рассмотрим каждый цвет по отдельности. Мы можем раздать все шарики цвета c друзьям Кефы только если c ≤ k. Потому что иначе, по принципу Дирихле, хотя бы один из друзей получит два или более шариков одинакого цвета.
Поэтому сделать нужно следующее: посчитать количество шариков каждого цвета, cntc.
А потом просто проверить, что cntc ≤ k для всех возможных c.
Сложность: O(N + K)

Находка — Bdiv2
(Автор: Mediocrity)

Первый игрок выигрывает, если в массиве есть хотя бы одно нечетное число. Давайте докажем это.
Обозначим суммарное количество нечетных чисел как T.
Тогда есть два случая:
1) T нечетное. Первый игрок может забрать весь массив и выиграть.
2) T четное. Предположим, что позиция самого правого нечетного числа pos. Тогда стратегия первого игрока такая: в первый свой ход, взять подотрезок [1;pos - 1]. Оставшийся суффикс будет иметь ровно одно нечетное число и второй игрок не сможет включить его в свой подотрезок. Поэтому, независимо от его хода, своим следующим ходом первый игрок заберет оставшиеся числа и выиграет.
Сложность: O(N)

Леха и функция — Adiv1
(Автор: Mediocrity)

Прежде всего, давайте поймем, чему равно значение F(N, K).
Для любого подмножества размера K, скажем, a1, a2...aK, мы можем уникальным образом сопоставить его с последовательностью d1, d2...dK + 1 так, что d1 = a1, d1 + d2 = a2, ..., .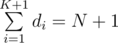
Нас интересует значение E[d1], матожидание d1. Зная основные факты о матожидании, мы можем получить следующее:
E[d1 + ... + dK + 1] = N + 1
E[d1] + ... + E[dK + 1] = (K + 1)·E[d1]
Отсюда немедленно следует, что .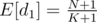
Теперь, значение 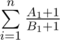максимизурется, когда A возрастает, B убывает. Это можно доказать при помощи транснеравенства.
Сложность: O(NlogN)

Леха и другая игра про графы — Bdiv1
(Авторы: 244mhq, totsamyzed)

Авторское решение опирается на тот факт, что граф связен.
Мы докажем, что искомое подмножество существует если и только если все  - 1 можно заменить на 0 / 1 так, что 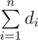четно. Если так сделать нельзя, то решения не существует (в каждом графе сумма степеней всегда четное число). Теперь мы покажем, как построить ответ для любого теста, где можно получить четную сумму.
Для начала, поменяем все  - 1 нужным образом.
Найдем любое остовное дерево и подвесим за любую вершину. Теперь задача стала гораздо легче.
Будем обрабатывать вершины одну за одной, в порядке глубины: от листьев к корню. Пусть текущая обрабатываемая вершина cur.
Есть два случая:
1) dcur = 0
В этом случае мы игнорируем ребро от cur до parentcur и забываем про вершину cur. Сумма степеней остается четной.
2) dcur = 1
В этом случае мы добавляем ребро от cur до parentcur в ответ, меняем значение dparentcur на противоположное и забываем про вершину cur. Как можно заменить, сумма меняет четность, когда мы меняем dparentcur, но потом снова становится четной, когда мы исключаем вершину cur. Поэтому в итоге сумма остается четной как и в первом случае.
Такими несложными манипуляциями мы получаем одно из возможных решений.
Сложность: O(N + M)

На скамейке — Cdiv1
(Авторы: Mediocrity, totsamyzed)

Разделим все числа на группы. Будем обрабатывать числа в порядке от 1 до N. Предположим, текущая позиция i. Если groupi еще не посчитано, i формирует новую группу. Присвоим уникальное число groupi. Потом для всех j таких, что j > i и a[j]·a[i] — квадрат, сделаем groupj равным groupi. Теперь произведение пары чисел дает квадрат если и только если они находятся в одной группе.
Можно использовать динамическое программирование для подсчета ответа.
F(i, j) будет обозначить количество способов расположить числа из первых i групп, образовав j плохих пар соседей.
Опишем переход из F(i, j). Обозначим размер следующей группы как size, а суммарное количество чисел, расставленных ранее, как total.
Переберем значения S от 1 до min(size, total + 1) и D от 0 до min(j, S).
S — количество кусков, на которое мы разобьем следующую группу, а D — количество существующих на данный момент плохих пар, которые мы разобьем.
Теперь добавим T к F(i + 1, j - D + size - S) (D пар разбито, size - S новых пар образовано после расположения чисел новой группы).
T — количество способов расположить числа новой группы согласно значениям S и D.
На самом деле, T есть 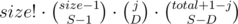. Почему? Потому что есть 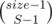способов разбить группу размера size на S кусков.
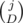способов выбрать D из j плохих пар, которые мы разобьем. И 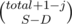способов выбрать расположения для S - D кусков (остальные D разбивают пары, так что их позиции определены).
После всех подсчетов, ответ находится в F(g, 0), где g — общее количество групп.
Сложность: O(N^3)

Судьба — Ddiv1
(Авторы: Mediocrity, totsamyzed)
Используем метод разделяй и властвуй.
Допустим, текущий запрос на отрезке [L;R]. Разделим массив на две части: [1;mid] и [mid + 1;N], где 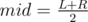. Если наш запрос целиком принадлежит левой или правой половине, перейдем туда и повторим процесс. Иначе L ≤ mid ≤ R. Мы утверждаем, что если сформировать множества из K самых часто встречаемых чисел в левой и правой половине, ответ либо будет в этом множестве либо его нет.

K самых часто встречаемых чисел можно предпосчитать. Запустим рекурсивную функцию build(node, L, R). Как при построении дерева отрезков, сначала зайдем в левого и правого сына node. Потом мы должны посчитать K самых часто встречаемых чисел для всех таких отрезков [L1;R1], что L ≤ L1 ≤ R1 ≤ R и хотя бы одно из L1 и R1 равно .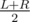

Рассмотрим все отрезки с левым концом в mid в следующем порядке: [mid;mid], [mid;mid + 1], ...[mid;R]. Если у нас уже были посчитаны K самых часто встречаемых и их количества для отрезка [mid;i], то же самое легко пересчитать для [mid;i + 1]. Мы обновляем счетчик для ai + 1 и смотрим, нужно ли что-то менять для нового списка.
То же самое делаем для отрезков с правой границей в mid. Обрабатываем в порядке [mid;mid], [mid - 1;mid], ..., [L;mid].
Теперь, заранее посчитав все это, мы можем запустить разделяй и властвуй и получить кандидатов на ответ в отрезке [L;R]. Чтобы проверить кандидата, мы можем заранее сохранить все вхождения каждого числа и потом использовать бинарный поиск для ответов на вопросы вида «Сколько раз x встречается на отрезке от L до R?»

Сложность: O(KNlogN)

В ловушке — Ediv1
(Автор: Mediocrity)
Путь от u до v можно разбить на блоки размером 256 вершин и (возможно) последний блок с меньшим количеством вершин. Этот последний блок рассмотрим отдельно, пройдя все его вершины в лоб. <br. Теперь нужно рассмотреть блоки длины 256. Каждый из них задается двумя числами: x — последняя вершина блока, d — 8 старших битов. Мы можем предпосчитать эти значения и использовать их для ответов на запросы.
Поговорим о предпосчете answer(x, d). Зафиксируем x и 255 вершин после x. Легко заметить, что младшие 8 битов всегда будут такими: 0, 1, ..., 255. Нужно закинуть в бор все значения 0 xor ax, 1 xor anextx и т.д.
Теперь, нужно перебрать все значения d от 0 до 255 и единственное, что остается сделать — найти в боре число, xor которого с 255·d дает максимальный результат.

Сложность: O(NsqrtNlogN)

  • Проголосовать: нравится
  • +66
  • Проголосовать: не нравится

»
7 лет назад, # |
  Проголосовать: нравится +2 Проголосовать: не нравится

Why a lot of likes for word "test".

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится +6 Проголосовать: не нравится

Can someone reword div1C/div2E ? What's the basic idea?

→ Ответить
  • »
    »
    7 лет назад, # ^ |
    ← Rev. 7   Проголосовать: нравится +13 Проголосовать: не нравится

    Through observation, we noticed that if a * b is a perfect square, b * c is a perfect square, the a * c is a perfect square too.So we can get T groups, and the problem changed to Source

    Solution from the site

    First we group all the distinct values in the array. Then we can solve the problem using dynamic programming:

    Let dp[i][j] = the number of distinct arrays that can be obtained using the elements of the first i groups such that there are exactly j pairs of consecutive positions having the same value. The answer can be found in dp[distinctValues][0].

    Now let's say the sum of frequences of the first i values is X. This means the arrrays we can build using the elements from these i groups have size X, so we can insert the elments of group i + 1 in X + 1 gaps: before the first element, after the last, and between any two consecutive. We can fix the number k of gaps where we want to insert at least one element from group i + 1, but we also need to fix the number l of these k gaps which will be between elements that previously had the same value. State dp[i][j] will update the state dp[i + 1][j — l + frequence[i + 1] — k].

    The number of ways of choosing k gaps such that exactly l are between consecutive elements having the same value can be computed easily using combination formulas. We are left with finding out the number of ways of inserting frequence[i + 1] elements in k gaps. This is also a classical problem with a simple answer: Comb(frequence[i + 1] — 1, k — 1).

    → Ответить
»
7 лет назад, # |
← Rev. 2   Проголосовать: нравится +11 Проголосовать: не нравится

For those who are having some difficulty understanding the above analysis of Div-1 C, there is a very similar problem on Codechef which has a very nice detailed editorial with explanation of the time complexity. :)

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится +5 Проголосовать: не нравится

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

In problem Destiny — Ddiv1. I don't understand this editorial : What is K most frequent values ?

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

In problem Destiny — Ddiv1. I don't understand this editorial : What is K most frequent values ?

If anyone understand this editorial, please explain for me ! Thank you !

→ Ответить
  • »
    »
    7 лет назад, # ^ |
      Проголосовать: нравится +29 Проголосовать: не нравится

    I also don't get it, but maybe it's using following neat algorithm to find majority elements.

    Problem: from a sequence of N elements find one that appears more than N/2 times.

    Solution: Repeat following: "Find two distinct elements and erase them.". If there is something left in the end, it will be all the same number and it's the only possible candidate for a solution.

    Now we can generalize:

    Problem: from a sequence of N elements find one that appears more than N/K times.

    Solution: Repeat following: "Find K distinct elements and erase them.". If there is something left in the end, it will be at most K-1 different numbers and they are only possible candidates for a solution.

    To use it in problem D we can apply the algoritm to interval [l, r] and obtain K-1 candidates for which we count number of appearances and obtain the answer.

    Applying the algorithm to an interval can be done using segment tree.

    → Ответить
    • »
      »
      »
      7 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      Why we should Find K distinct elements and erase them. I don't understand. Can you explain again for me ?

      → Ответить
      • »
        »
        »
        »
        7 лет назад, # ^ |
        ← Rev. 3   Проголосовать: нравится +5 Проголосовать: не нравится

        Let's talk about K=2. If we repeat deleting two distinct numbers from the sequence, in the end, we'll have at most one distinct number.

        Now, imagine that in the original sequence there is a number that appears more than N/2 times. It's impossible that all its appearances will be killed by the algorithm.

        Why? Because every time we want to erase one of its appearances we also have to erase one other number. And we won't be able to do it because this number appears more times than all others combined. Thus, it will be the number that's only left at the end of the algorithm.

        This doesn't mean that generally number that's left in the and appears more than N/2 times, but only that if there is such a number it will be left at the end of the algorithm.

        Generalizing to K>2 shouldn't be hard once you get K=2.

        → Ответить
»
7 лет назад, # |
  Проголосовать: нравится +18 Проголосовать: не нравится

There is another solution to problem D, with the same complexity (O(KNlogN)), using a wavelet tree (http://mirror.codeforces.com/blog/entry/52854). Build the wavelet tree for the input array. Queries are then handled similarly to "count the number of occurrences of x in [L,R]" queries, but instead of picking a branch depending on a number x, we explore both branches, but cut branches with less than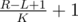 elements. At each level of the tree, at most K branches will remain, so a query is handled in time O(KlogN).

My code : 29654756. I only had to write the solve and main functions, and the solve function was obtained from cnt.

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Can Div1 D be solved with Mo's algo somehow without TLE?

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Still waiting for Div1 E.

→ Ответить
»
7 лет назад, # |
← Rev. 5   Проголосовать: нравится +22 Проголосовать: не нравится

Since the editorial for Div-1 E is not yet available, I decided to explain my solution to it on the basis of this comment.

Each mask can consist of atmost 16 bits. We deal with both halves separately. For a given query (u, v), we process the path in blocks of 256. For any vertex on the path from u to v (let it be a), the distance from v will be of the form 256*A+B, where A>=0 and 0<=B<256. If we process the path in blocks of 256, the "A" values for all vertices in the block will be same.

Note that 256*200 > 50000, so there will be atmost 200 blocks. We precompute for each vertex, considering it as the lowest vertex of the block, for all i such that 0<=i<=200, what the max XOR we can get using the most significant 8 bits. If you see my code,

best_most_significant_eight[v][i] denotes the max xor we can get considering only the most significant 8 bits in the block of size <= 256, with the lowest vertex being v and i is the "A" value of the vertices in this block. eg. For a node at distance 257 (256*1+1) from node v, the "A" value is 1.

Now, we need to handle the lowest 8 bits. For any block, we should consider the lowest 8 bits of only those nodes whose highest 8 bits give us the max xor obtained previously. This we can do using precomputation too. Again, with reference to my code, best_lower_significant_eight[v][i] denotes the max xor we can get using lower 8 bits (i.e. using the "B" value) for the block with lowest vertex v and the highest 8 bits are i.

We can calculate best_lower_significant_eight[][] by just iterating over the immediate 256 ancestors of every vertex.

We can calculate best_most_significant_eight[][] by inserting all the values of the immediate 256 ancestors in the trie and then querying for the max XOR, for all i from 0 to 200.

Now all that remains is to handle the vertices in the topmost (maybe incomplete) block while solving a query. In that case, since there are atmost 256 vertices to check, we can just run through them all and update our answer.

You can see my code for this implementation. Time complexity is roughly O(N*256 + Q*256).

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Can someone please explain Leha and function — Adiv1 ?

→ Ответить
  • »
    »
    7 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    One important step is to prove F(N,K) = (N+1) / (K+1).

    For any subset of size K, we sort them as a_1, a_2, ..., a_K with a_1 < a_2 < ... < a_K. Here we construct another sequence which is d_i, d_1 = a_1, d_2 = a_2 — a_1, ..., d_K = a_K — a_{K-1}. Note the sequence {d_i} and sequence {a_i} are bijection.

    We add another d_{K+1} = N + 1 — a_K. Note d_i are identically distributed, which means if we switch any two of d_j, d_k and keep other d unchanged, the correspoding {a_i} is still valid (Only the value of a_j changed).

    So E(d_1) = E(d_2) = ... = E(d_{K+1}).

    Also, we have E(d_1 + d_2 + ... d_{K+1}) = N+1. So E(d_1) = (N+1) / (K+1).

    Since a_1 is the smallest of a_i, due to definition, we have F(N,K) = E(a_1) = E(d_1) = (N + 1)/(K + 1).

    What left is just to Google "rearrangement inequality".

    → Ответить
    • »
      »
      »
      5 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      I would have expected that we need to calc F(N,K) somehow and use these values. It seems that this is not necessary. Why?

      → Ответить
»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Hi! Can anyone please explain this sample test case from Div2D.

Input:

4 5
0 0 0 -1
1 2
2 3
3 4
1 4
2 4

Output:

0

0 output means that there are no edges in the good subset and the original graph already satisfies all the mentioned conditions( for every vertex i, di =  - 1 or it's degree modulo 2 is equal to di. ).

In this graph:

deg[1]=2, di[1]=0 (2%2==0[satisfied])
deg[2]=3, di[2]=0 (3%2!=0[ `how is this satisfied?` ])
deg[3]=2 di[3]=0 ([satisfied])
deg[4]=3 di[4]=-1 (di[4]=-1,[satisfied])

Moreover, if I remove 5th edge(2 4) then all conditions are satisfied but that would be a Wrong Answer.

Can anyone point me in the right direction? I am unable to understand this question.

Thanks :)

→ Ответить
  • »
    »
    7 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    As you said 0 means there are NO EDGES in the good subset. There are only the vertices, i. e. every node's degree is 0, which satisfies the conditions.

    → Ответить
»
7 лет назад, # |
← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

по-моему так, в разборе к див1С забыли к T домножить F(i,j)

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Can anyone please explain Div2-D/Div1-B ? I didn't understand the solution given in the editorial.

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Can someone please explain how to solve div 2 C or div 1 A.

→ Ответить
»
7 лет назад, # |
← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

Hello,

The statement in the editorial Adiv1 "as Benq stated in his comment",

so where can I find Benq's comment?

Thanks in advance.

→ Ответить
»
6 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

can someone please help me understand div1 A . i learnt what is meant by expected values but i am unable to understand the proof given in the editorial . Please help

→ Ответить
  • »
    »
    5 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    Hello! I don't know if you are still interested in this problem, but I'd like to share my thought with you. As you can see in the tutorial, any element $$$a_i$$$ in the set with size of $$$k$$$, can be represented by an array $$$d$$$, where $$$\sum\limits_{j=1}^{i}d_i=a_i$$$. And let's denote $$$\sum\limits_{i=1}^{k+1}d_i = N + 1$$$. Obviously, $$$d_i$$$ is identically distributed, which means $$$E(d_1) = E(d_2)=....=E(d_{k+1})$$$. Because of the linearity of expectation, $$$N+1=E(\sum\limits_{i=1}^{k+1} d_i)=\sum\limits_{i=1}^{k+1}E(d_i)$$$,and it's equal to $$$(k+1)E(d_1)$$$. So $$$E(d_1)=\dfrac{N+1}{K+1}$$$. Feel free to ask me if you still have any question!

    → Ответить
    • »
      »
      »
      5 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      Why are $$$ d_i $$$ identically distributed?

      → Ответить
      • »
        »
        »
        »
        5 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится

        Because all $$$d_i$$$ have the same possiblity to be $$$1,2,....,N-1$$$.They are symmetric and equivalent.

        → Ответить
        • »
          »
          »
          »
          »
          5 лет назад, # ^ |
            Проголосовать: нравится 0 Проголосовать: не нравится

          Do you have a rigorous proof? Seems kinda handwavish to me.

          → Ответить
          • »
            »
            »
            »
            »
            »
            5 лет назад, # ^ |
              Проголосовать: нравится 0 Проголосовать: не нравится

            Hmm... I think it's rigorous enough. Is there anything not clear enough?

            → Ответить
            • »
              »
              »
              »
              »
              »
              »
              5 лет назад, # ^ |
              ← Rev. 11   Проголосовать: нравится 0 Проголосовать: не нравится

              Well, on 70th edit i think i got kinda close to the rigorous proof.

              Let's compute possible values for $$$ d_s, 1 \leq s \leq k $$$. You must have $$$ \sum_s d_s = N + 1 $$$ and you already used up $$$ s - 1 $$$ of them, which implies that you only have $$$ N + 1 - (s-1) = N - s + 2 $$$ left. $$$ d_r, s < r \leq k + 1 $$$ must be positive too. Let's suppose they are all $$$ 1 $$$ to maximize $$$ d_s $$$. There are $$$ k + 1 - s $$$ of them, so that gives you a maximum of $$$ N-s+2 - k - 1 + s = N-k+1 $$$ for $$$ d_s $$$. Note that it does not depend on $$$ s $$$, so at least possible range is the same for all of them.

              I still don't get why expectations are the same though.

              → Ответить
              • »
                »
                »
                »
                »
                »
                »
                »
                5 лет назад, # ^ |
                  Проголосовать: нравится 0 Проголосовать: не нравится

                The upper bound of $$$d_i$$$ is $$$N+1-K$$$.It's not that important...... Assume that you have gotten an array {$$$d_i$$$}. Then you can exchange $$$d_1$$$ and $$$d_2$$$,it will form a new {$$$d_i$$$}. So for any number $$$d_1$$$ can be,$$$d_2$$$ can also have the same possibility to be that number. Similarly, all $$$d_i$$$ have the same possibility to be a specific number. So I say it's symmetric...Then according to the definition of expectation:$$$E(x)=\sum i*P(x = i)$$$,you can know their expectations are equal.

                → Ответить
»
5 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
Another approach for D:
→ Ответить
»
4 года назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

DIV 1 A can easily be done as Printing largest element of a parallel with the smallest element of b then the 2nd largest element parallel with the 2nd minimum of b and so on.. 83756733

→ Ответить
»
4 года назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Can problem Div1 D (Destiny) solved using a persistent segment tree ? I tried but I'm getting WA on test 6 which makes me think the logic is wrong? I'm not sure if it's just a bug somewhere. https://mirror.codeforces.com/contest/840/submission/115038909

Sorry for the necropost!

→ Ответить