OpenCup — GP of Belarus

12 лет назад, # |

А какой сервак там стоит? На моем старом ноуте 4-летней давности задача I работает 1.5 секунд. Утверждается, что TLE = 2 секунды. WTF?

→ Ответить

caustique

12 лет назад, # ^ |

Решение динамикой на O(NR) работает мгновенно. Какое решение у вас?

→ Ответить

12 лет назад, # ^ |

Ну мы то за куб написали, но дело в том, что старенький ноут делает это за 1.5 секунды, а Core 2 Quad, который раза в два мощнее, не сумел это сделать за 2 секунды.

→ Ответить

AndreySiunov

12 лет назад, # ^ |

← Rev. 2 →

Ну дк на старом наверное одно ядро, а на новом 4, каждое из которых будет послабее, на одном из которых работает программа.

→ Ответить

12 лет назад, # ^ |

У меня дома на десктопе такой процессор, так что у меня есть пруф, что он в 2 раза быстрее ноута

→ Ответить

12 лет назад, # |

B: Гарантировать можно, посчитав всё точно, у авторов же бесконечное время. Ключевой кусок зашедшего кода:

} else {
	int P = 100 - Q;
	double u = Math.pow(p, A + B) - Math.pow(q, A) * Math.pow(p, B);
	double v = Math.pow(p, A + B) - Math.pow(q, A + B);
	double res = A * (1 - u/v) - B * (u/v);
	if (Double.isNaN(res)) {
		res = Q > 50 ? A : -B;
	}
	res *= Q + P;
	res /= Q - P;
	out.printf("%.20f\n", Math.abs(res));
}

→ Ответить

12 лет назад, # ^ |

← Rev. 2 →

Эм.... A + B ~ 10^9, никакой Math.pow не сработает. Утверждение "если A+B большое, то надо брать A или B" — неверно (ну или я что-то в этой жизни не понимаю). Что-то у меня появляются сильные сомнения, что у авторов всё хорошо...

Upd: ну т.е. мы считали в BigDecimal'ах с точностью 600, возводя матрицы в степень. Наши ответы были абсолютно стабильны, но наше решение не зашло.

→ Ответить

12 лет назад, # ^ |

Да, мне тоже не нравится это утверждение. Ждём комментариев тех, кто решил с плюса. Не зашло именно по WA?

→ Ответить

12 лет назад, # ^ |

Хм, проверил — для самого "страшного" теста ответ, вычисленный таким образом, совпадает с нашим. Так что утверждение может и верно, но каким образом у нас WA — я не понимаю.

→ Ответить

12 лет назад, # ^ |

А у вас работает для A = B = 10⁹ и p = 1, а также для p = 99? Ответы должны совпадать.

→ Ответить

12 лет назад, # ^ |

Ага, работает. Но нашёлся тест, на котором отличается от формулы на 1E-8, даже если её в BigDecimal переправить. Так что видимо с нашим решением теряется слишком много точности, чтобы BigDecimal её компенсировал (мы не знали явной формулы, поэтому у нас линейная реккурентность с возведением матрицы в степень). Значит, в итоге мы не правы, а авторы правы :( Ограничения конечно тоже жестокие — зачем просить такую жуткую точность, чтобы только знающие явную формулу загнали? Ну да ладно.

Всем спасибо за помощь :)

→ Ответить

12 лет назад, # ^ |

У нас возведение матрицы 3х3 в степень с BigDecimal. Прошло с первого раза.

→ Ответить

12 лет назад, # ^ |

Ну понятно, что это зависит от матрицы. Например, мы делали так: у нас есть трёхдиагональная система уравнений, выражаем всё через x₁; всё выражается с помощью коэффициентов a_k, b_k, которые преобразуются линейным образом и считаются матрицей в степень (5x5). В итоге получаем x₁ и ещё одним возведением в степень считаем x_A. Вот тут 700 знаков BigDecimal уже не хватило, как выяснилось :(

→ Ответить

12 лет назад, # ^ |

У нас примерно то же самое, только матрица 3х3. Если записать уравнение для x_i, то легко выразить x_i через линейную комбинацию x_i - 1, x_i - 2 и константы. А это считается матрицей 3х3. Но вообще, можно же не зная формулы заранее, развернуть рекуррентность и вывести эту формулу. Правда, для 5х5 это довольно неприятно.

У нас, кстати, во всех операциях с BigDecimal используется MathContext.DECIMAL128. Я подозреваю, это далеко не 700 знаков.

→ Ответить

yaro

12 лет назад, # ^ |

В каком смысле "только знающие явную формулу загнали"? Мы, например, решали задачу как упражнение на вывод этой самой формулы. Линейная рекуррента выражает решение через корни квадратного уравнения, переход с вероятности на мат. ожидание (та самая плюс единица) — линейная поправка c * i для члена f_i.

→ Ответить

natalia

12 лет назад, # ^ |

+13

У нас возведение матрицы 3x3 в степень. Решаем систему d_i = 1 + p·d_i - 1 + (1 - p)d_i + 1 методом прогонки: d_i - 1 = α_i + β_i·d_i.

$\text{[math]}$ , $\text{[math]}$

Дальше записываем α_i = a_i / c_i, β_i = b_i / c_i, строим линейную систему относительно a_i, b_i, c_i и возводим матрицу в степень. После каждой операции умножения проделываем нормировку (делим все элементы матрицы на наибольший по модулю элемент). Прошло с первого раза в long double.

→ Ответить

12 лет назад, # ^ |

Поздравляю с победой. 9 задач — это очень круто!!!

→ Ответить

ivan.popelyshev

12 лет назад, # ^ |

Тоже поздравляю с победой, я восхищён :)

→ Ответить

12 лет назад, # ^ |

Ну да, это похоже на то, что у нас, но проще. И видимо точнее, раз у вас в long double'ах зашло, а у нас BigDecimal'ы умерли из-за того, что p на 100 в даблах поделили :)

P.S. Поздравляю с победой, ваша команда в этом сезоне пока адски жжёт.

→ Ответить

12 лет назад, # ^ |

Илья, матрицу из даблов инициализировал?

→ Ответить

12 лет назад, # ^ |

О, точно в цель! p / q считал в BigDecimal'ах, а вот p с самого начала на 0.01 в даблах умножил :( Обидная бага, и главное — её было вполне реально найти. Спасибо.

→ Ответить

12 лет назад, # ^ |

Отлично, что разобрались. А вот сразу в теги писать bugs как-то зло. Правда в итоге баги участников. Как говорит мой сын "бивает..."

→ Ответить

12 лет назад, # ^ |

Опс, сорри, убрал bugs :)

→ Ответить

12 лет назад, # ^ |

Да, кстати, если задачу решает формула, состоящая из арифметических действий, то оценка точности всего лишь дело техники, разве нет?

→ Ответить

12 лет назад, # ^ |

Эм... тест "50 1000000000 1000000000" — ваше решение выводит "-Infinity". Либо у вас написано что-то интересное вне этого else, либо я говолюсь говорить авторам много чего доброго...

→ Ответить

12 лет назад, # ^ |

Вне этого "else" написано вот что, я просто не хотел загромождать пост

int Q = nextInt();
double q = Q * 0.01;
double p = 1 - q;
int A = nextInt();
int B = nextInt();
if (Q == 0) {
	out.println(B);
} else if (Q == 100) {
	out.println(A);			
}		
else if (Q == 50) {
	out.println(A * (long)B);

→ Ответить

12 лет назад, # ^ |

Вроде ваше решение в BigDecimal не заходило из-за неправильной инициализации: BigDecimal.valueOf(P / 100.0) — неправильно; BigDecimal.valueOf(P).divide(BigDecimal.valueOf(100)) — правильно.

→ Ответить

ivan.popelyshev

12 лет назад, # ^ |

Блин, я это отсёк как явно бредовый вариант :)

→ Ответить

Sasha_Grey

12 лет назад, # |

В задаче H надо было считать С-шки? или там был какой-то другой трюк ?

→ Ответить

bayleef

12 лет назад, # ^ |

C-шки считать надо было. Во всяком случае, в нашей динамике они активно использовались.

→ Ответить

http://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B0_%D0%BE_%D1%80%D0%B0%D0%B7%D0%BE%D1%80%D0%B5%D0%BD%D0%B8%D0%B8_%D0%B8%D0%B3%D1%80%D0%BE%D0%BA%D0%B0

12 лет назад, # |

← Rev. 2 →

-10

ВНЕЗАПНО задача В очень известная, например, на википедии:

Примечание: формулы явные, проблемы с точностью не намечаются.

→ Ответить

12 лет назад, # ^ |

E и F тоже не блещут оригинальностью. Как википедия помогает добиться нужной точности в B?

→ Ответить

12 лет назад, # ^ |

Написал update. Там просто конструктивная формула, в которой в условиях задачи нет вычитания близких чисел.

→ Ответить

scorpion

12 лет назад, # |

Как решать "runs" and "palindroming"?

→ Ответить

bayleef

12 лет назад, # ^ |

+11

runs — квадратная динамика, говорящая, с какой вероятностью перестановка из i элементов имеет j серий. Надо заметить, что когда мы вставляем в перестановку длины i с j сериями элемент i+1, то в i-j-1 месте количество серий увеличивается на 2, в двух местах — на 1, а в оставшихся j местах не меняется. Таким образом имеем квадратную динамику с пересчётом значения за константу.

→ Ответить

http://pastebin.com/gAnzkTRB

12 лет назад, # ^ |

У нас кубическая динамика прошла. Динамика по количеству поставленных элементов, количеству серий и последнему элементу. Каждый раз вставляем элемент в конец и пересчитываем все при помощи частичных сумм.

→ Ответить

sankear

12 лет назад, # ^ |

Хм... писал ровно такую динамику, но у меня WA 42 все время! Не подскажете, в чем ошибка?

→ Ответить

Zhukov_Dmitry

12 лет назад, # ^ |

Ошибка на тесте 1 1?

→ Ответить

sankear

12 лет назад, # ^ |

Спасибо!

→ Ответить

bayleef

12 лет назад, # ^ |

← Rev. 2 →

palindroming можно делать так. Понятно, что ответ зависит только от количества вхождений каждой буквы в слово. Посчитаем их в массив a[26]. Теперь, чтобы найти количество перестановок чётной длины, можно поделить каждый элемент из a пополам и решить задачу про количество слов, которые можно составить из этих букв. Это можно сделать динамикой d[i][j]-количество слов из первых i букв длиной j. Пересчёт динамики получается такой: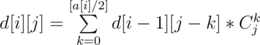 $\text{[math]}$

Для нечётной длины всё почти то же самое, только необходимо выбрать какую-то букву на роль центральной и убрать её вхождение из а. Таким образом получаются ещё 26 подсчётов.

→ Ответить

yarrr

12 лет назад, # |

А что по E (факториалы) заходило?

→ Ответить

12 лет назад, # ^ |

+24

Прога на хаскеле мгновенно решает :) Т.к. там длинка хорошо реализована.

→ Ответить

hydrastuff

12 лет назад, # ^ |

А хаскел доступен? В дорешивании его нет, и на opencup.ru в Server Parametrs тоже отсутствует.

→ Ответить

12 лет назад, # ^ |

Хм, в дорешивании действительно почему-то нет. Но на контесте был.

→ Ответить

12 лет назад, # ^ |

← Rev. 4 →

+11

У нас зашло такое. Пусть мы хотим перемножить набор из N чисел (изначально это {1, 2, ..., N}). Разделим это множество на 2. В первом будут элементы с нечетными индексами, во втором — с четными. Рекурсивно посчитаем ответ для меньших множеств. Теперь при помощи БПФ перемножим получившиеся ответы.

→ Ответить

Zhukov_Dmitry

12 лет назад, # ^ |

← Rev. 2 →

Можно было точно так же, но ответы перемножать за квадрат. Заходило по времени после оптимизации 'не умножать a[i] на b[j], если хотя бы одно из этих чисел равно нулю (a[i] и b[j] — "цифры" длинных чисел)'.

Точнее у нас отрезок из чисел [l, r] разбивался на отрезки [l, m] и [m + 1, r], где m = (l + r) / 2. Но с чётными-нечётными индексами по идее должно ещё быстрее работать.

→ Ответить

12 лет назад, # ^ |

Выложи код, пожалуйста

→ Ответить

http://pastebin.com/jDZ9zF48

12 лет назад, # ^ |

→ Ответить

12 лет назад, # ^ |

← Rev. 2 →

Вижу два основных отличия от моего: цвет автора и своя структурка вместо complex<double>. Наверное, все таки первое.

→ Ответить

PavelKunyavskiy

12 лет назад, # ^ |

Вообще complex тормозит.

→ Ответить

12 лет назад, # ^ |

← Rev. 3 →

Окей, буду знать. В Петрозаводске мы сдавали две задачи с complex<double>, и все нормально заходило, да и на емаксе про это ничего не написано...

→ Ответить

_dangerous_

12 лет назад, # ^ |

не всегда все что на емаххе хорошо, да и вообще там про это написано

→ Ответить

_dangerous_

12 лет назад, # ^ |

← Rev. 2 →

писать FFT на стандартном comlex, тоже самое что бинпоиск по эпсилону — рано или поздно будешь покаран за это, ага

→ Ответить

12 лет назад, # |

+95

Как представитель авторов прошу плюсовать/минусовать этот комментарий. В ответ прошу высказаться по задачам: оригинальность, сложность, интересность.

→ Ответить

12 лет назад, # ^ |

Нормальный контест, не то чтобы очень крутой, но и не ужасный (а таких в последнее время очень много). По поводу оригинальности — F и G конечно не стоило давать, E пожалуй тоже, там языки с нормальной встроенной длинкой имеют большое преимущество; с B проблема, что про это есть статья в wiki, но не думаю, что много кто в процессе контеста её там нашёл.

По поводу интересности — D, I и B достаточно интересные; над C и J во время контеста не успел особо подумать, к сожалению.

→ Ответить

qwaker.00

12 лет назад, # ^ |

На этих задачах проводился чемпионат БГУ (1/8 ACM) где без F, G совсем бы было туго, а языки с хорошей длинкой не принимаются.

→ Ответить

12 лет назад, # ^ |

+12

Спасибо. По поводу F, G и других хочу высказать свое мнение:
1) это была олимпа БГУ, не только кубок
2) это не онсайт для профи, тут нужны и упражнения, и сложные интересные задачи, если убрать A, F, G и H (которые не сказать, что супер задачки), то слишком много команд получает около нуля АС. Это хорошо? Но, конечно, топ не тратил бы время на [:||||:], а решал бы только новые и интересные для них задачи
3) лично мне больше всего нравятся задачи B, C, J и вообще не нравится F, но... см. выше
4) B: про статью в wiki мы не знали, но у нас было два принципиально разных решения
5) Е: мы просто не знали, что можно решить стандартными средствами, но и так она не фантастическая, но довольно оригинальная ИМХО
6) G: лично я уверен, что на примере этой задачи можно показывать, как хорошо повернуть систему координат и сделать задачу много проще
7) I: у нас было решение только за куб... круто, что участники смогли решить за квадрат

→ Ответить

12 лет назад, # ^ |

Ну ок, с поправкой на чемпионат БГУ претензий нет, хороший контест. (btw, по поводу G — поскольку в кубке теперь разрешён prewritten code, решения с поворотом и без абсолютно одинаковы.)

→ Ответить

it4.kp

12 лет назад, # ^ |

По поводу I: http://oeis.org/A059427

там рекуррентная формула дана, с которой решается за квадрат

→ Ответить

gojira

12 лет назад, # ^ |

+24

По поводу F — неужели венгерский алгоритм или MCMF в наше время считаются настолько простыми, что задача на них даётся как утешительная?

А задача H, в отличие от F и G, лично мне показалась оригинальной и понравилась.

→ Ответить

12 лет назад, # ^ |

Я тоже не думаю, что много кто нашел ее во время контеста. Я читал эту статью с год назад, там интересные следствия о корректности рискованных стратегий в худшей позиции.

→ Ответить

Gerald

12 лет назад, # ^ |

← Rev. 2 →

+12

Очень интересно, есть ли в задаче J решение без миллиона формул. Я честно потратил час, на то чтобы все их вывести, но к сожалению забыл частный случай, на который требовалось еще столько же формул =( поэтому за 40 минут до конца забил на нее.

Можно ли как-то оригинальнее? Если да, расскажите хотя бы в двух словах, пожалуйста.

UPD. Забыл сказать, что хотел. Контест очень понравился, сбалансированный хороший контест. Побольше бы таких OpenCup. Большое спасибо всем авторам.

→ Ответить

12 лет назад, # ^ |

Числа в прямоугольнике можно разбить на 4 треугольника, для каждого из которых решать будет одну и ту же задачу: найти сумму в пересечении треугольника и прямоугольника.
Как решать такую задачу: треугольник и прямоугольник пересекаются тремя схожими областями, для каждой из которых будет подбирать многочлен.
Легко заметить, что многочлен зависит от количества строк и столбцов в матрице и количества столбцов в сумме. Но количество строк и столбцов у нас константа! Тогда нужно сгенерить несколько первых членов суммы, и потом подобрать многочлен только от количества слагаемых.
Думаю, что, внимательно прочитав, можно уже решение додумать.
Лично у меня около 170 строк на java в BigInt :)

→ Ответить

12 лет назад, # ^ |

Понравились задачи B и D. Хотя, подозреваю, в D есть более простое решение, чем то что мы сдали. Авторское решение тоже основано на слиянии приоритетных очередей (используя трюк с перебрасыванием из меньшей в большую) и работает за O(Nlog²N)?

По поводу самых простых задач. Если в G можно найти хоть какой-то поучительный смысл, то задачу F вообще не понимаю. Можно было хотя бы матрицу сделать прямоугольной. Для тех кто и так нормально умеет писать венгерский алгоритм или MCMF, это ничего бы не изменило, зато для команд которые писали его впервые после прочтения Кормена или еще чего-то, добавило бы хоть какой-то элемент размышления.

→ Ответить

12 лет назад, # ^ |

Нет. В авторском дихотомия.

→ Ответить

Fefer_Ivan

12 лет назад, # ^ |

В D? По какому параметру вообще?

→ Ответить

Joshik

12 лет назад, # ^ |

+13

По вероятности, к которой "стремимся" — все, которые меньше ставим на r[i], которые больше — l[i], остальные — на эту вероятность. Считаем сумму и соответственно двигаем границу бинпоиска.

→ Ответить

rizar

12 лет назад, # ^ |

Ключевое наблюдение — все вероятности, не стоящие на нижних (верхних) границах должны быть равны одному числу X. Доказывается дифференцированием. Далее, существует единственное X, при котором сумма вероятностей будет равна 1. Ищем его дихотомией.

→ Ответить

Fefer_Ivan

12 лет назад, # ^ |

← Rev. 2 →

Лол. У нас вообще другое решение. Ну тоже за n log n.

→ Ответить

rizar

12 лет назад, # ^ |

Поделись :)

→ Ответить

Fefer_Ivan

12 лет назад, # ^ |

Присвоим каждой переменной значение left_i. Отсортируем все переменные по этому значению. Теперь пусть у нас есть сэт активных переменных. Это переменные, значение которых мы будем одновременно увеличивать. Причем текущее значение всех переменных одинаковое. Сэт меняется в двух случаях.
1. Когда какая-то переменная из сэта достигает знаенчия right_i. Тогда она удаляется.
2. Когда значение перенных в сэта достигает значения left_j какой-то переменной не из сэта. Тогда она добавляется.

Если мы можем увеличить текущее значения до следующего изменения сэта так, что сумма < 1, то увеличиваем. Иначе увеличиваем на (1 — sum) / (размер сэта) и выходим из цикла.

Как-то так.

→ Ответить

rizar

12 лет назад, # ^ |

Клево. Но по сути вы ищете ту же равновесную точку X, что наше авторское искало дихотомией. Я пытался написать перекрест в духе вашего решения, но когда оказалось, что это сложнее, чем я думал, забил. :)

→ Ответить

12 лет назад, # ^ |

+12

Задачи хорошие, хотя и правда достаточно много известного и повторов.

Например, задача С была на отборе в Казань года четыре назад, но там реализации больше, чем идеи. Правда, вполне возможно, что я — единственный, кто из нынешних участников opencup решал тот отбор.

→ Ответить

MikeMirzayanov

12 лет назад, # ^ |

Туда эту задачу позаимствовали с каких-то древних сборов школьников.

→ Ответить

12 лет назад, # ^ |

Да, причем тематических. Там было пять задач вида "нарисовать граф на чем-то". К сожалению, найти те сборы сейчас не получилось.

→ Ответить

Romchela

12 лет назад, # |

Расскажите, пожалуйста, как решалась задача M?

→ Ответить

Slamur

12 лет назад, # ^ |

Решим в два этапа.

1 этап — отсечем те числа, которые точно нам не подходят. Для этого будем отсекать по одной рамке спирали. С каждой рамкой размеры оставшейся матрицы будут уменьшаться на 2, а координаты нужной клетки — на 1. Видно, что влоб отбрасывать нельзя.

Попробуем отбросить все ненужные рамки сразу. На каждой рамке написано 2 * n + 2 * m — 4 — 8 * (index — 1), index — номер рамки. Тогда полное количество чисел, которые точно можно отбросить, равно 2 * k * (n + m) — (4 + 12 + 20 + ... + (4 + 8 * (k — 1)) = 2 * k * (n + m) — 4 * k * k, k — количество отброшенных рамок.

Заметим, что k = min(i — 1, j — 1, n — i, m — j). Значит мы можем отбросить 2 * k строк, 2 * k столбцов, координаты i, j также уменьшаются на k.

2 этап — просто проверить принадлежность точки (i, j) к четырем сторонам текущей рамки матрицы. Проверять надо в порядке заполнения, то есть левая сторона/нижняя/правая/верхняя. Искомая клетка точно будет на одной из этих сторон, так как все внешние по отношению к ней клетки мы отбросили на 1 этапе.

→ Ответить

pva701

12 лет назад, # |

немного не в тему: кто-нибудь знает, можно ли изменять составы команд и название команды, или первичные регистрационные данные нельзя изменять? если можно, правильно я понимаю, что нужно написать письмо с просьбой snarknews?

→ Ответить

12 лет назад, # ^ |

Изменить точно можно. Писать думаю должен координатор региона.

→ Ответить

Avitella

12 лет назад, # ^ |

Нужно написать координатору, инфа 100%. Мы сделали именно так.

→ Ответить

perec1970

12 лет назад, # |

А как же решается задача А о расстоянии между точками на прямоугольниках?

→ Ответить

Hohol

12 лет назад, # ^ |

Строим граф из всех интересных точек, пускаем по нему флойда.

→ Ответить

perec1970

12 лет назад, # ^ |

Если я правильно понял, то нужно найти точки пересечения прямоугольников. По ним и вершинам прямоугольника построить граф.

→ Ответить

Hohol

12 лет назад, # ^ |

Да. Ну еще точки старта и финиша.

→ Ответить

Avitella

12 лет назад, # ^ |

Подскажите, пожалуйста, простой способ построения графа к этой задаче. У меня не вышло. Видимо я шел по неверному пути, у меня там вылезало очень много строчек кода, в следствии чего до конца контеста ее дописать не удалось.

→ Ответить

pva701

12 лет назад, # ^ |

ну там он вроде один, по другому не напишешь: добавляем все нужные точки, аккуратно пересекаем в целых числах все стороны прямоугольников, потом перебираем две точки, если они обе лежат на какой-то стороне какого-то прямоугольника (всего 8), кидаем между точками ребро. пускаем флойда. профит.

→ Ответить

Avitella

12 лет назад, # ^ |

Спасибо. Я делал оказывается совсем по дурацки, стыдно распространяться :)

→ Ответить