It can be observed that n people will consume 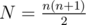 elements. Thus, we should first compute the remainder m%N, and then find out the maximum i so that
elements. Thus, we should first compute the remainder m%N, and then find out the maximum i so that 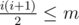 . The answer is
. The answer is 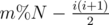 .
.
This is a simulation problem. We start from the end of the binary sequence, and enumerate the digit one by one. If we meet a “0”, then do nothing; otherwise we simulate the binary addition of adding “1” to the current position. When the sequence reduces to a single “1”, the number of total operations is just the answer.
To construct the second string while using the the minimum number of the first string, we can adopt the greedy algorithm.
Specifically, we maintain a variable S, which is set to - 1 initially. For any letter appearing in the second string, we should find the same letter in the first string with the smallest index i satisfying i > S. Then, we update S = i. When we can not find the required i, it implies that we have to start from the beginning of the first string again, which will set S = - 1. This also means that the number of the first string should be added by one.
To implement the above algorithm, we can store the positions of each letter in previous, in an increasing order. Thus, we can use binary search to find out the smallest index i satisfying i > S.
This is a classic “inversal pair” problem, but asking to find out the farthest “inversal pair”.
The basic idea is using suffix, specifically, suffix minimum index. For the original array a[n], we use b[n] to denote its suffix minimum index, i.e., b[i] gives the index from i to n - 1 so that a[b[i]] is the minimum value among a[i], a[i + 1], a[i + 2], ..., a[n - 1]. Furthermore, as there may exist duplicate values, b[i] should be the maximum index if there are several equal minimum values.
Next, to find the farthest inversal pair of a[i], we can implement binary search among b[i], b[i + 1], ..., b[n - 1] and find out the largest b[j] so that a[i] > a[b[j]] holds. The binary can succeed since b[i] is a nondecreasing sequence.
Well, I can only come up with a “not so strict” proof...
We adopt a variable a with initial value equal to 1. Whenever we find that the currently added edge belongs to a connected component, we multiply a by 2 (remember to calculate the modulo), and output the answer a - 1.
To prove the correctness of the above formula, we divide all the edges into two types S and T, with the former one containing the edges that do not belong to any components while the latter one containing the edges belonging to some component. If we remove all the edges from T, then the graph reduces to several unconnected components, and thus no ski base can be built. As we add edges from T, the graph “begins” to contain at least one component. As we have 2|T| ways to choose edges from T, we can have 2|T| - 1 ski bases. The term “-1” comes from the empty case, where no edges from T are selected, since this leads to no ski base.









