Let's discuss problems.
By the way, finally reached #1!

| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
| Название |
|---|



How to solve problem 900
Ok, I have some ideas, and my solution passes system tests in practice room, but not sure if it's correct.
The idea of my solution is that if we look at each rook as an edge between (row i) and (col j), then the graph should not have a cycle. Additionally, when we pair the rooks up, there should be at most one pair on each row and each columns.
Also, we should not introduce any new pairs of rooks. Then for each existing rook, we decide if it will be contained in a row pair, or a column pair (2^20 possibilities), and check if there is a way to make a matching without violating the above conditions.
I had the same idea as you and I wrote a straightforward mask dp and got TLE(actually RE because there were too many statuses)
Actually, I didn't really bother checking if there was a valid matching at all.
I only checked a condition on whether the number of rooks you need is strictly less than the total number of rows and columns (otherwise, there must be a cycle)
However you have to not let rows / columns which contain no rooks at the end count towards your total.
The only thing I was short of you was that I didn't notice "we should not introduce any pairs of rooks."
Let's construct a graph with n red vertices and m blue vertices. For each '#' add an edge between corresponding vertices. Then we get a bipartitely colored forest. Now we want to add some edges between vertices of different colors, and satisfy the following:
The final state will look like the following. Black edges are newly added edges. Other colors represent original components.
When the final state satisfies the conditions above, black edges can be uniquely assigned to one of colored components. For example, in the previous example, edges 1, 2, 3 should be assigned to green, purple, and orange, respectively. Look at the following picture:
We want to connect node a with some blue node, node b with some red node, and node c with some red node. It doesn't really matter which red/blue nodes to choose. We just need to make sure that we don't form any cycles.
Thus, we try all subsets of vertices that have "tails" (in the example above we chose three nodes a, b, c). Check the conditions 2 and 3. For these conditions, the choice of nodes with question marks doesn't matter.
Can we satisfy the condition 1? For this, it is important to distinguish two types of components: a component with at least two nodes (it always have both red and black) and an isolated vertex. Let rneed, bneed be the number of red/blue question marks, rsingle, bsingle be the number of red/blue isolated vertices, and let comp be the number of non-isolated components. Then, it's not hard to prove that a valid assignment is possible if and only if max(rneed - rsingle, 0) + max(bneed - bsingle, 0) ≤ comp - 1.
Big congratulations on advancing and on #1!
My sad story: challenge phase, open a big solution, think "it's so big, surely it has a bug", challenge blindly, get -25, get 7th place instead of 5th :(
My sad story: Medium failed on 1 test out of 280 cause it runs 2.1s (TL=2s). Get 12th place instead of 4th.
Btw, I am not sure how arena works in such cases. Are you sure that your code gave correct answer after 2.1s or did arena just kill your solution after that?
I had execution time approximately 5s when I tested inefficient solution. And it passed after some minor optimisations. But I can't be sure of anything in arena :)
;)
Heyy! No screencast since long :(
Everything alright??
How to solve 500 properly without things like "if we add this pruning heuristic to our backtrack then it seems that it fits in TL on systests, but no idea why"?
I'm sorry, looks like I accidentally send the comment, good version of the comment is below.
Can you describe that MITM approach? I had no idea how to make use of that technique. I think I figured out bruteforce that should handle k>=9 but didn't know what to do with smaller k values.
I will describe it for k = 8 (for simplicity).
I want to check all the variants of choosing 8 items. I'll divide them into two halves such that all the items from the first half is to the left to all the items from the second. Now let's fix the fifth item (the leftmost in the second half). Now I want to generate all the variants to take 4 items to the left to the fixed position (it will be the first half), then generate all the variants to take remaining 3 items to the right and for each variant of the second half count the number of good variants of the first half. For example, we can generate all possible sums in the first half, then sort them and use binary search. But it will be slow. Instead of sorting and binary search, we can use Fenwick tree (values are up to 4·107, so we have enough memory) and notice that we can move our fixed fifth item one position to the right easily: we only need to add new variants of the first half with forth item in the rightmost possible position. Now this soltuion works in time I mention earlier.
Nice idea, I hoped that n^k/2 should be doable but was silly enough to think only about dividing all values into two halves which was obviously not working. All in all, that was pretty hard problem, but as for med of TCO3 it was just right.
For k ≤ 8 we can do meet-in-the-middle, I've used Fenwick tree here, number of operations is about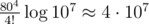 . For k > 8 real value of d is no more than 5·107 and much smaller if k > 9, so for now I will say that k = 9 is the worst case. We will sort all the values from big to small and then do a bruteforce the following way:
. For k > 8 real value of d is no more than 5·107 and much smaller if k > 9, so for now I will say that k = 9 is the worst case. We will sort all the values from big to small and then do a bruteforce the following way:
I didn't prove it properly, but I'm pretty sure that every O(k) steps I will reduce D by 1, so the number of operations is about 5·108.