Hello CodeForces !
We have an array with n integers and Q query. each query has 4 integers L1 , R1 , L2 , R2 such that (1 <= L1 <= R1 < L2 <= R2 <= n) and for answer to query we should print the number of distinct numbers in [L1 , R1] U [L2 , R2] !
I want to answer each query online :)
limits :
1 <= n , Q <= 10 ^ 5
1 <= a[i] <= 3 * (10 ^ 5)
GoodLuck :))
PS a[i] <= 3 * (10 ^ 5) maybe it can help us :))))
PS2 dacin21 solved this problem with an interesting solution :) thanks all











The query can be transoformed into (number of distinct elements in [L1;R2]) — (number of distinct elements in [R1 + 1;L2 - 1] which don't occure in [L1;R1] and [L2;R2]).
The first part is the well known SPOJ D-query and the second one can be solved by dividing the elements in heavy and light by the number of their occurrences (lets consider numbers heavy if their occurrences in the whole array are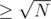 and light overwise).
and light overwise).
The number of heavy groups is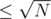 so for every query we can check if every heavy number satisfies the second part of the inital query (in O(1) or
so for every query we can check if every heavy number satisfies the second part of the inital query (in O(1) or 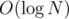 ).
).
Now for the light numbers it will be a bit trickier. For each light group we can itterate over all pairs of numbers (because the group size is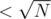 ). To solve the light group part we will consider every pair of positions and add a tuple (i, j, lsamei, rsamej), where i is the left position of the pair, j is the right one, lsamei is the closest position to the left with same number and rsamei. Now to answer the query we need the number of tupples with
). To solve the light group part we will consider every pair of positions and add a tuple (i, j, lsamei, rsamej), where i is the left position of the pair, j is the right one, lsamei is the closest position to the left with same number and rsamei. Now to answer the query we need the number of tupples with 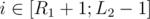 ,
, 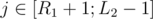 , lsamei < L1 and rsamei > R2. And so the building of the structure will be
, lsamei < L1 and rsamei > R2. And so the building of the structure will be 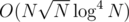 and the query will be in
and the query will be in 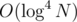 if we do a 4d Fenwick. If we change the size of the consideraton of the groups (currently
if we do a 4d Fenwick. If we change the size of the consideraton of the groups (currently 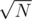 ) we can achieve
) we can achieve 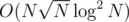 for building and
for building and  for query for the light.
for query for the light.
And so here is a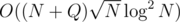 solution.
solution.
PS: We actually can use another structure for the light queries which looks like a 2d Fenwick with a persistent segment tree in it. This way the building and query will be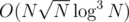 and
and 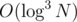 . With careful choosing of the size of consideraton of the groups we can achieve a
. With careful choosing of the size of consideraton of the groups we can achieve a 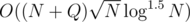 solution.
solution.
PS2: The chance of this solution being a complete overkill isn't small.
wow ! the solution confused me a lot :)
maybe I have to read it many times and maybe a code can help me in understanding :)
can you ( or anybody else ) share its code please ?
But the time complexity near to N * Q.
yes ! For N = 10 ^ 5 and Q = 10 ^ 5 time is 182 seconds :|
Actually the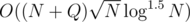 solution will do about 2 billion operations and should be able to run in about 5-10 seconds if implemented well, while the O(NQ) will do about 20 billion operations (which are simple though). I'm not sure if you are able to pass below a minute with the O(NQ) solution.
solution will do about 2 billion operations and should be able to run in about 5-10 seconds if implemented well, while the O(NQ) will do about 20 billion operations (which are simple though). I'm not sure if you are able to pass below a minute with the O(NQ) solution.
Naive O(NQ) runs 12.5 seconds on CF servers, and I think I can make it work less
than 5than 10 seconds. But I'm really not sure that you can implement your solution so that it will run for less than 10 seconds =)How do you know? Is this problem anywhere on CF? No link is provided in the blog
Custom Invocation. My code: https://pastebin.com/6w5EgaTj
Doesn't codeforces custom invocation kill solutions after they have ran over 10 seconds?
It does. But I run for Q = 10k, 50k, 70k, etc, As my code runs O(N) per query you can easy calculate the time for 100k =)
btw, I think I have easy O(NlogN). Will describe in 1-2 hour, when come homeI was wrong. Sorry.No the problem formed in my mind :)))
https://pastebin.com/KBKQrDMw
~5 seconds with O(NQ)
I know O((N + Q) * log2(N) ^ 3) solution :)
UPD1: Building O(N * log2(N) ^ 3), Query O(log2(N) ^ 3)
Can you share it?
Auto comment: topic has been updated by nima10khodaveisi (previous revision, new revision, compare).
A solution in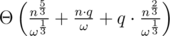 with bitset should be squeezable, assuming the memory limit is large enough. (ω, the word size, is usually 32 or 64).
with bitset should be squeezable, assuming the memory limit is large enough. (ω, the word size, is usually 32 or 64).
Compress the ai to be in [0, n - 1]. Let be the block size. For every pair
be the block size. For every pair 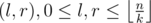 precompute a bitset storing
precompute a bitset storing 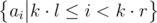 . This takes
. This takes 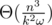 time and memory.
time and memory.
To get the bitset of any range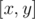 , let
, let 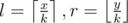 . Get the precomputed bitset for (l, r), then add the values in a[] from x to min(y, k·l) and from max(x, k·r) to y into the bitset. This takes Θ(k) time per query.
. Get the precomputed bitset for (l, r), then add the values in a[] from x to min(y, k·l) and from max(x, k·r) to y into the bitset. This takes Θ(k) time per query.
The answer to any query is (get_bitset(l1, r1) | get_bitset(l2, r2)).count(). This takes
is (get_bitset(l1, r1) | get_bitset(l2, r2)).count(). This takes 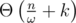 time per query.
time per query.
A factor 2 could be optimized by considering numbers that appear only once in a separately, which cuts the size of the bitset in half.
Edit: fixed formula for k.
oh okay :) interesting solution :))))
But I think time is not ok :)
But I think memory is not ok :)
maybe problem hasn't better solution :)
It is ok actually. The memory will be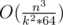 where k is the block size. This way we can set k to
where k is the block size. This way we can set k to  to fit the memory limit. This way our time complexity will increase by a constant factor but it won't be a big constant (about 2 or 3).
to fit the memory limit. This way our time complexity will increase by a constant factor but it won't be a big constant (about 2 or 3).
Thanks for commenting with the proper memory consumption (should be fixed now).
Custom test runs in 1715 ms, using 125'192 KB (without the optimisation)
Actually the number of operations for given constraints is about 300 million simple operations which should run in less than 3 seconds (it can be even faster).
oh yes you are right :)
thanks all :)))))