First change all the letters into lower case ones, and then compare the two strings as the problem requires.
To cut the whole board into two symmetric parts, the cutting line must pass through the central point. Therefore, the following four squares can not be special cells, i.e., (n, n + 1), (n, n), (n + 1, n), (n + 1, n + 1), where (r, c) denotes the r-th row and the c-th column.
I did not figure out how to prove this, however it turns out that the following solution can pass all the tests.
At first, note that if 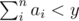 can satisfy the requirement, then
can satisfy the requirement, then 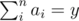 can satisfy as well. Thus, we set a1 = a2 = ...an - 1 = 1 and an = y - n + 1, which gives the maximum value of
can satisfy as well. Thus, we set a1 = a2 = ...an - 1 = 1 and an = y - n + 1, which gives the maximum value of 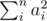 . Moreover, if y < n, then the answer is definitely “-1”; otherwise we divide y as mentioned above and check the result is no less than x or not.
. Moreover, if y < n, then the answer is definitely “-1”; otherwise we divide y as mentioned above and check the result is no less than x or not.
For each integer n, it takes complexity  to obtain all its divisors. For each divisor, we should check whether it is divisible by any one of the previous y integers. Thus, we can use an array idx[n] to record the maximum index of the given integer that has n as its divisor. When we deal with the current i-th query, we find out each of its divisor x, and check idx[x] to determine whether this divisor satisfies the requirement or not. Next, we update idx[x] = i, since x is divisible by the i-th integer.
to obtain all its divisors. For each divisor, we should check whether it is divisible by any one of the previous y integers. Thus, we can use an array idx[n] to record the maximum index of the given integer that has n as its divisor. When we deal with the current i-th query, we find out each of its divisor x, and check idx[x] to determine whether this divisor satisfies the requirement or not. Next, we update idx[x] = i, since x is divisible by the i-th integer.
Update-1: proof of 112C - Petya and Inequiations
Given a1 + a2 + ... + an = D where only positive integers are involved and D ≥ n, the maximum value of a12 + a22 + ... + an2 is (n - 1) + (D - (n - 1))2 with a1 = a2 = ... = an - 1 = 1 and an = D - (n - 1), i.e., the optimal sequence can have at most one positive integer that is greater than 1.
Proof: We prove this claim by contradiction. Assume that the optimal sequence has more than one positive integer that is greater than 1, and we denote them as x and y, with x > 1 and y > 1. Then, we write s1 = x2 + y2 and s2 = 12 + (y + x - 1)2, and one can see that the term s2 means that we set x = 1 while "moving" a quantity of x - 1 to y. Next, s2 - s1 = 1 + (y + x - 1)2 - x2 - y2 = 1 - y2 + (y - 1)(y + 2x - 1) = (y - 1)(y + 2x - 1) - (y - 1)(y + 1) = 2(y - 1)(x - 1) > 0. Thus, we have obtained a larger (better) value since s2 > s1 and this is contradictory to our assumption, which completes the proof.









