I have been thinking about this problem for quite some time now but I am stuck and I cannot find a feasible solution for this one. The equation has become really ugly for me and it seems messy. So, please can anyone help me on how to solve this problem? Thanks in advance.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 19.11.2024 15:36:13 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










Any help now???
Let x = (x1, x2, ..., xn) represent our solution, xi is the velocity for i-th section (according to the hint, we will always ride with uniform velocity on one section).
It only makes sense to consider solutions with xi > max(0, vi). Also there's always an optimal solution where we use all our energy, because if we have some energy left, we can increase velocity somewhere and we'll arrive faster.
Let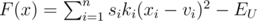 . We'll consider only solutions satisfying F(x) = 0 because we want to use all our energy. Let
. We'll consider only solutions satisfying F(x) = 0 because we want to use all our energy. Let 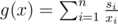 . We want to optimize g while respecting the constraint F(x) = 0.
. We want to optimize g while respecting the constraint F(x) = 0.
Lagrange multipliers tell us that for optimal solution there exists some λ, such that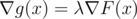 , so for every i we have xi2(xi - vi)ki = C (where
, so for every i we have xi2(xi - vi)ki = C (where 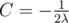 ).
).
For given C we can solve this equation using binsearch (left side is increasing if xi > max(0, vi). We can also observe that if we increase C, then the solution x(C) will also increase and so F(x(C)) will also increase. So we can binsearch for such C that F(x(C)) = 0 and this will give us optimal x.