AtCoder Regular Contest 085 / AtCoder Beginner Contest 078 held on Saturday, 21:00 UTC+9.
Let's discuss about the contest.
Sorry for announcing too late. (Actually, no one write about this so I wrote this blog.)
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3885 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3580 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3506 |
| 7 | ecnerwala | 3505 |
| 8 | Radewoosh | 3457 |
| 9 | Kevin114514 | 3377 |
| 10 | gamegame | 3374 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 170 |
| 2 | -is-this-fft- | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 160 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 153 |
| 8 | luogu_official | 152 |
| 8 | awoo | 152 |
| 10 | maomao90 | 148 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/02/2025 23:21:39 (i2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











How to solve A(from ARC)? I only managed to solve D :C
Any hints for D?
Let's modify the game:
This modification is equivalent to the original game and has only O(n^2) states with O(1) transitions from each state.
Note that the last card must be chosen by one of the players.
Let dp[i][j] be the answer if the last move played was player j taking card i. We'll only consider dp[i][j] when 0 ≤ i ≤ n - 2.
To calculate dp[i][j], we iterate over all possible next card x ≤ n - 2 the next player can take and maximize (or minimize) the current value with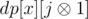 . Also, it is possible the next player takes the last card immediately, which makes the answer abs(a[i] - a[n - 1]).
. Also, it is possible the next player takes the last card immediately, which makes the answer abs(a[i] - a[n - 1]).
Finally, at the beginning, player 1 either takes the last card immediately or we can iterate over all the cards player 1 takes and read the corresponding dp value. Time complexity is O(n2). Note that the value of A is irrelevant for this problem.
UPD : Apparently with the observation from the first line you can easily see that the answer is min(|B - a[n - 1]|, |a[n - 2] - a[n - 1]|) lol.
.
To solve HSI, you can use the same logic described in this answer on stack overflow:
Expected value of rolling dice until getting a 3
My submission: http://arc085.contest.atcoder.jp/submissions/1763234
How to solve F (currently there is no editorial).
Sort the intervals (A[i], B[i]) such that B[i] <= B[i+1]. Now, you can do simple DP in O(n^2), dp[i] means that interval i is the last one chosen for the solution.
However, this is too slow. We have two options:
Cheat the task: try only 500-1000 best values of DP and update from them.
Actually solve the task: first of all, let our current interval be (a, b). With non-intersecting intervals (x, y) helps a simple segment tree, result is maxDP(1, a-1) + sum(a, b). Intersecting intervals are harder. Note that if they are entirely covered by our current interval using them is nonsense (like, they don't change anything). So we should only consider transitions from intervals (x, y) such that (1 <= x <= a-1) and (a <= y <= b). 2D structure helps in this case, because there is an easy way to compare two intervals and see which one is going to give us a better DP result.
Complexity of the solution: O(n log^2). I suspect there is an easier way...
Yes, I have an O(NlogN) solution. It's exactly as yours from what I've seen broadly in your description. The only difference is that you don't need to have 1<=x<=a-1 and a<=y<=b, you only need x<a<=y (actually it works if you put x<=a<=y) because b is always increasing, so at each point the already considered intervals have y <= b. Also, 1<=x for any x. So under that form it becomes obvious that we can use a simple segment tree where we update interval [x+1, y] or [x, y] (if you wish to consider the equality case — doesn't really matter) and query a position. It works with lazy propagation (actually you don't even need to hold anything in the segment tree itself, only to know the lazy value, because you have queries only at certain positions, so you go down to a leaf).
My solution is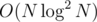 (treating Q as N for simplicity) but I heard from my friend that there's
(treating Q as N for simplicity) but I heard from my friend that there's 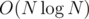 solution.
solution.
Let's precompute the number of zeroes in each prefix so we can know how many zeroes there are in an arbitary range [l, r] in O(1) time.
Let suf[i] be the minimum hamming distance we can get if we only consider the substring [i, n - 1] and also use operations with l ≥ i. Our answer is suf[0].
We calculate suf[x] from n - 1 to 0. Additionally, for each segment [l, r] we assign to it a value v which indicates that if we consider the substring [l, n - 1] and color [l, r] then the minimum hamming distance we can get is v.
To calculate suf[x], we can either not do anything to the x-th bit, and thus the answer will be suf[x + 1] + (a[x] = = 1) or we can choose one of the intervals starting from the i-th bit and color the range. Let's say we color the range [x, y]. We iterate over all range [l, r] with l > x, r > y and assume we color [l, r] next. The cost in this case is the answer for [l, r] + number of zeroes in range [x, l - 1] = answer for [l, r] + pre[l - 1] - pre[x - 1], where pre[i] is the number of zeroes in [0, i].
How to optimize this? We can call the cost of a segment [l, r] as the sum of answer for [l, r] and pre[l - 1]. Then, for each segment, we don't have to iterate over all relevant segments but instead lookup the best answer with a segment tree where each node is a segment tree. Time complexity is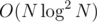 and memory complexity is
and memory complexity is 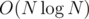 .
.
I manage to solve Problem D: ABS. But I am still not sure whether my logic was correct or the test cases were weak. Please help.
Finally I understood. The above code is same as
Is this solution for C correct?
Problem C can be reduced to minimum closure problem. The closure condition is "If you choose vertex i, then you must also choose vertex 2 * i, 3 * i".
To solve the minimum closure problem, you can negate all the weight of the diamond ai = - ai) and it will become the maximum closure problem.
To solve the maximum closure problem, add two vertices s and t. For each i, if ai is positive, create edge (s, i, ai), otherwise create edge (i, t, - ai). For each i, create edge (i, k * i, ∞) with 2 ≤ k ≤ n / i. Then the answer to the original problem is the sum of all diamond with positive weight (before negating all the diamond) minus the weight of the minimum s - t cut of the above graph.
Yes this is precisely my solution.
It turned that I got WA not because the algorithm is wrong, but because I made another "genius" piece of code in my Dinic flow implementation.
I should have copied the Dinic flow implementation instead of trying to code it myself...
Lol, I got AC for problem E with O(2n / 2) bruteforce(with some pruning of course)
Nice))
my simple bruteforce passed too.
i just considered the cases i*2>n and i*3>n
runs 685 ms
My solution for ARC-E (MUL):
Letting a = ⌊ n / 4⌋, I've solved it in O(A051026(a) * nlgn) where A051026(n) is n-th term in http://oeis.org/A051026 .
First, brute-force whether choose x = 1, 2, 3, ..., a. It seems like it has O(2a) combinations, but if you use the idea of "if x = p is chosen, choosing x = kp (k ≥ 2) doesn't change the answer".
If you decide whether choose x = 1, 2, 3, ..., a or not, respectively, the "component of multiple/divisor" (in val > a) is only 2k - 3k - 4k - 6k, k - 2k - 3k, k - 2k and k. You can calculate the answer respectively so you can calculate the answer in O(n) in sum. So it got AC.
Code: https://beta.atcoder.jp/contests/arc085/submissions/1763980
By the way, why Emilbek doesn't write announcement blog recently?
Sorry. Next time I will write. Thank you E869120 for assisting me
can anyone agree with me ! if the problem was calculate all differences on each step the solution of dp dosent change ?